Термодинамическая система
объектов, lg м
тумане — 5·10-6
Земли — 1,5·1011
звезды альфа Центавра — 4·1016
туманности Андромеды — 1022
Термодинами́ческая систе́ма — физическое тело (совокупность тел), способное (способных) обмениваться с другими телами (между собой) энергией и (или) веществом[1]; выделяемая (реально или мысленно) для изучения макроскопическая физическая система, состоящая из большого числа частиц и не требующая для своего описания привлечения микроскопических характеристик отдельных частиц[2], «часть Вселенной, которую мы выделяем для исследования»[3]. Единицей измерения числа частиц в термодинамической системе обычно служит число Авогадро[4] (примерно 6·1023 частиц на моль вещества), дающее представление, о величинах какого порядка идёт речь. Ограничения на природу материальных частиц, образующих термодинамическую систему, не накладываются: это могут быть атомы, молекулы, электроны, ионы, фотоны и т. д.[5][6]. Любой земной объект, видимый невооружённым глазом или с помощью оптических приборов (микроскопы, зрительные трубы и т. п.), можно отнести к термодинамическим системам: «Термодинамика занимается изучением макроскопических систем, пространственные размеры которых и время существования достаточны для проведения нормальных процессов измерения»[5]. Условно к макроскопическим системам относят объекты с размерами от 10−7 м (100 нм) до 1012 м[7].
Условность нижней границы связана, помимо прочего, с тем, что для термодинамики важен не размер объекта, а число образующих его частиц. Куб идеального газа с ребром 100 нм при нормальных условиях содержит около 27 000 частиц (см. Постоянная Лошмидта).
Рабочее тело[K 1], представление о котором используют в технической термодинамике, есть пример термодинамической системы.
Абсолютно твёрдое тело с термодинамической точки зрения представляет собой одну-единственную частицу и по этой причине вне зависимости от своих размеров к термодинамическим системам не относится[9].
Галактические и метагалактические системы термодинамическими не являются[10].
Любую часть термодинамической системы называют подсистемой.
Для описания термодинамической системы используются макроскопические параметры, характеризующие не свойства составляющих её частиц, а свойства самой системы: температуру, давление, объём, магнитную индукцию, электрическую поляризацию, массу и химический состав компонентов и др.[11][12].
Каждая термодинамическая система имеет границы, реальные или условные, отделяющие её от окружающей среды[13], под которой подразумевают все тела, не включённые в термодинамическую систему[14]. Иногда вместо окружающей среды говорят о термостате[5], т. е. среде с настолько большой теплоёмкостью, что её температура при теплообмене с изучаемой системой не меняется[15][16][17]. По умолчанию предполагается, что окружающая среда достаточно велика и поэтому её параметры не зависят от протекающих в рассматриваемой системе процессов. Кроме того, обычно подразумевается, что окружающая среда находится в состоянии термодинамического равновесия и её характеристики не зависят от времени и пространственных координат.
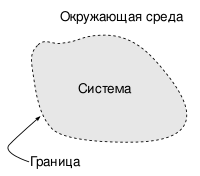
Важно, что в состав термодинамической системы включают все частицы, имеющиеся в выделяемой для изучения области пространства. Дело в том, что в термодинамике иногда мысленно разбивают реальную физическую систему на самостоятельные подсистемы объектов с особыми свойствами, и один и тот же объём рассматривают как занимаемый одновременно двумя и более виртуальными квазинезависимыми (слабо взаимодействующими друг с другом) парциальными подсистемами частиц разной природы (например, газовую смесь характеризуют парциальными давлениями составляющих её газов[18]; в газовой плазме одновременно присутствуют ионы и свободные электроны со своими существенно отличными парциальными температурами — ионной и электронной[19][20]; в кристалле выделяют подсистемы фононов и магнонов; подсистему ядерных спинов парамагнетика характеризуют собственной парциальной спиновой температурой [21], способной принимать отрицательные значения по шкале Кельвина[22][23][24]). Данный формальный приём позволяет вводить для рассматриваемой подсистемы частиц парциальные характеристики, не обязательно имеющие прямое отношение к физической системе как единому целому (см., например, Отрицательная абсолютная температура).
Термодинамические системы служат предметом изучения термодинамики, статистической физики и физики сплошных сред.
Классификация термодинамических систем


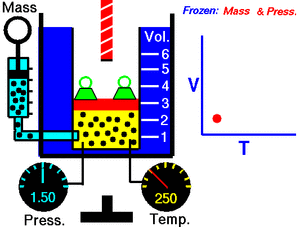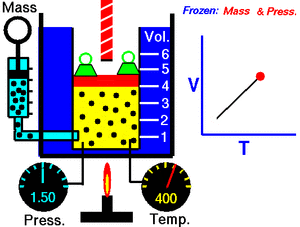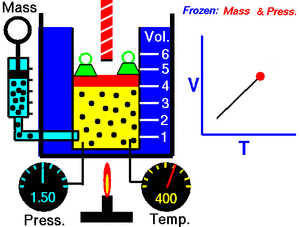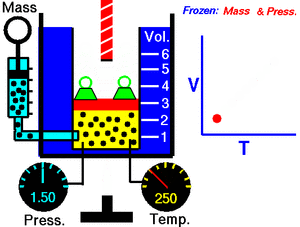


По внутренним процессам различают системы[25]
- пассивные, в которых происходит перераспределение имеющейся энергии, например тепловой, стремящиеся к равновесному термодинамическому состоянию;
- активные, в которых происходит преобразование одного вида энергии в другой, например химической в тепловую, стремящиеся к неравновесному термодинамическому состоянию
По характеру взаимодействия с окружающей средой различают системы[13]:
- изолированные, не способные обмениваться с внешней средой ни энергией, ни веществом[1];
- адиабатно изолированные, не способные к обмену с внешней средой веществом, но допускающие обмен энергией в виде работы[26][27][28][29]. Обмен энергией в форме теплоты для таких систем исключён[1][30][31][32];
- закрытые, не способные обмениваться с внешней средой веществом[1], но способные к энергообмену с окружающей средой[33];
- открытые, способные обмениваться веществом (и, следовательно, энергией) с другими системами[33][34] (внешней средой);
- частично открытые, обменивающиеся с внешней средой веществом, но при этом не все составляющие вещества принимают участие в материальном обмене (например, из-за наличия полупроницаемых перегородок)[35].
По используемым для термодинамического описания системы параметрам состояния различают: простые системы, простые открытые системы и сложные системы.
- Простой системой (простым телом[36], термодеформационная система[37]) называется такая равновесная система, физическое состояние которой вполне определяется значениями двух независимых переменных — функций состояния простого тела [math]\displaystyle{ (x,y) }[/math], например, значениями температуры и удельного объёма [math]\displaystyle{ (t,v) }[/math] или давления и удельного объёма [math]\displaystyle{ (P,v) }[/math]. Выражение зависимости трёх характеристик состояния простого тела [math]\displaystyle{ (x,y,z) }[/math], являющихся попарно независимыми, называется уравнением состояния этого тела:
[math]\displaystyle{ \varphi(x,y,z)=0 }[/math].
Простыми телами являются изотропные тела (isos— равный, tropos — направление, в целом — равенство характеристик состояния и физических свойств тела во всех его точках и во всех направлениях), в частности: газы, пары, жидкости и многие твёрдые тела, находящиеся в термодинамическом равновесии и не подверженные действию поверхностного натяжения, гравитационных и электромагнитных сил и химических превращений. Исследования простых тел в термодинамике представляют наибольший теоретический и практический интерес.
- простые открытые системы, отличаются от простых систем способностью обмениваться веществом с окружающей средой. Для термодинамического описания таких систем с [math]\displaystyle{ k }[/math] независимыми компонентами необходимы [math]\displaystyle{ k + 2 }[/math] независимых параметра состояния, включая массу (количество вещества, число частиц) каждого независимого компонента[38];
- сложными системами называют все термодинамические системы, не попадающие под определения простых систем, и простых открытых систем. К сложным системам принято относить диэлектрики, магнетики, сверхпроводники, упругие твёрдые тела, поверхности раздела фаз, системы в поле тяготения и в состоянии невесомости, электрохимические системы, равновесное тепловое излучение. Некоторые авторы в число сложных включают и простые открытые системы[39]. Для термодинамического описания таких систем, как упругий стержень/нить или пружина, поверхность раздела фаз, тепловое излучение необходим только один независимый параметр состояния[40].
Если входящие в состав системы вещества в рассматриваемом диапазоне условий (давление, температура) химически не взаимодействуют между собой, то систему называют физической. Если же вещества системы реагируют друг с другом, то говорят о химической системе[41][42][43].
Реальную изоляцию термодинамической системы от окружающей среды осуществляют посредством стенок (поверхностей раздела, перегородок, оболочек)[44]: подвижных и неподвижных, проницаемых и непроницаемых для вещества (существуют и полупроницаемые перегородки). Сосуд Дьюара служит хорошим примером[45] адиабатной (термоизолирующей[46]) оболочки. Перегородка, не препятствующая теплообмену, то есть не являющаяся адиабатной, называется диатермической[47][48] (теплопроницаемой[49]).
Поскольку для открытых систем трактовка понятий «работа» и «теплота» теряет свою однозначность[50], то и представление об адиабатности утрачивает определённость. Чтобы восстановить определённость и сохранить эквивалентность представления об адиабатной изоляции как накладывающей запрет на теплообмен, и адиабатной изоляции как допускающей энергообмен только в форме работы, для открытых систем к теплоте и работе добавляют третью форму передачи энергии — энергию перераспределения масс составляющих систему веществ [51][52][53][54], а свойства адиабатной оболочки дополняют требованием непроницаемости оболочки для вещества[55][56][57][58][29][32]. К сожалению, такой способ восстановления однозначности трактовки понятия «адиабатность», широко используемого в технической термодинамике, одновременно делает представление об адиабатности бесполезным с практической точки зрения в случае открытых систем, так что в химической термодинамике таких систем понятие «адиабатность» не используют.
Термодинамическую систему называют гомогенной, если между любыми её частями нет поверхностей раздел[1] и, следовательно, свойства системы непрерывно изменяется от точки к точке[59]. Гомогенную систему с одинаковыми свойствами в любой точке называют однородной[59][1]. Примерами гомогенных систем служат растворы (газовые, жидкие и твёрдые). Газовая фаза большой протяжённости вдоль градиента поля тяготения (например, земная атмосфера в безоблачный и безветренный день) — пример неоднородной гомогенной фазы (см. Барометрическая формула).
Термодинамическую систему называют гетерогенной, если она состоит из нескольких гомогенных частей с разными свойствами. На поверхностях, разделяющих гомогенные части гетерогенной системы, хотя бы одно термодинамическое свойство вещества изменяются скачком[60][1]. Часто (но не всегда) поверхность раздела является видимой.
Гомогенную часть гетерогенной системы называют фазой[60]. Менее строго, но более наглядно фазами называют «гомогенные части системы, отделённые от остальных частей видимыми поверхностями раздела»[12]. Примером может служить система «лёд — вода — влажный воздух». Гомогенная система содержит только одну фазу; гетерогенная система состоит из двух или более фаз[61]. Число фаз в гетерогенной системе подчиняется правилу фаз Гиббса. Одно и то же вещество в твёрдом агрегатном состоянии может иметь несколько фаз (ромбическая и моноклинная сера, серое и белое олово и др.)[60].
На рисунке изображён один из вариантов классификации термодинамических систем.

См. также
Комментарии
- ↑ Под рабочим телом применительно к двигателям понимают вещество (газ, жидкость, твёрдое тело), с помощью которого энергия, выделяющаяся при сгорании органического топлива и в ядерных реакциях из ядерного топлива, преобразуется в полезную механическую работу[8].
Примечания
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 6.
- ↑ Физическая энциклопедия, т. 5, 1998, с. 84.
- ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 9.
- ↑ Квасников И. А., Термодинамика, 2002, с. 17.
- ↑ 5,0 5,1 5,2 Кубо Р., Термодинамика, 1970, с. 11.
- ↑ Базаров И. П., Термодинамика, 2010, с. 206.
- ↑ Хачкурузов Г. А., Основы общей и химической термодинамики, 1979, с. 8.
- ↑ Куприков М. Ю., Реактивный двигатель, 2015.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 40.
- ↑ Скаков С. В., Техническая термодинамика, 2014, с. 6.
- ↑ Физика. Большой энциклопедический словарь, 1998, с. 521.
- ↑ 12,0 12,1 Герасимов Я. И. и др., Курс физической химии, т. 1, 1970, с. 27.
- ↑ 13,0 13,1 Пригожин И., Кондепуди Д., Современная термодинамика, 2002, с. 18.
- ↑ ГОСТ Р 57700.4-2017 Численное моделирование физических процессов. Термины и определения в областях механики сплошных сред: гидромеханика, газовая динамика, с. 4.. Дата обращения: 18 июля 2018. Архивировано 18 июля 2018 года.
- ↑ Базаров И. П., Термодинамика, 2010, с. 40.
- ↑ Козлов В. В., Ансамбли Гиббса и неравновесная статистическая механика, 2008, с. 171.
- ↑ Путилов К. А., Термодинамика, 1971, с. 101.
- ↑ Физика. Большой энциклопедический словарь, 1998, с. 522.
- ↑ Белонучкин В. Е. Краткий курс термодинамики, 2010, с. 160.
- ↑ Франк-Каменецкий Д. А., Лекции по физике плазмы, 1968, с. 53.
- ↑ Спиновая температура — статья из Физической энциклопедии
- ↑ Спиновая температура — статья из Большой советской энциклопедии
- ↑ Ландау Л. Д., Лифшиц Е. М., Статистическая физика. Часть 1, 2002, с. 262.
- ↑ Поулз Д. Отрицательные абсолютные температуры, 1964.
- ↑ Доброборский Б.С. Безопасность машин и человеческий фактор / Под ред. д.т.н., проф. С.А. Волкова. — СПб.: СПбГАСУ, 2011. — С. 33 - 35. — 114 с. — ISBN 978-5-9227-0276-8. Архивная копия от 20 января 2022 на Wayback Machine
- ↑ Новиков И. И., Термодинамика, 1984, с. 8.
- ↑ Хейвуд Р., Термодинамика равновесных процессов, 1983, с. 56.
- ↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 73—74.
- ↑ 29,0 29,1 Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 10.
- ↑ Эткинс П., де Паула Дж., Физическая химия, ч. 1, 2007, с. 51.
- ↑ Хачкурузов Г. А., Основы общей и химической термодинамики, 1979, с. 20.
- ↑ 32,0 32,1 Вукалович М. П., Новиков И. И., Термодинамика, 1972, с. 20.
- ↑ 33,0 33,1 ГОСТ IEC 60050-113-2015 Международный электротехнический словарь. Часть 113. Физика в электротехнике (IEC 60050-113:2011, IDT), с. 17.. Дата обращения: 18 июля 2018. Архивировано 16 июля 2018 года.
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 120—121.
- ↑ Белоконь Н. И., Основные принципы термодинамики, 1968, с. 12.
- ↑ Гухман А. А., Об основаниях термодинамики, 2010, с. 66.
- ↑ Мюнстер А., Химическая термодинамика, 1971, с. 141.
- ↑ Сычев В. В., Сложные термодинамические системы, 2009, с. 257.
- ↑ Сычев В. В., Сложные термодинамические системы, 2009.
- ↑ Компоненты (в термодинамике и химии) // Большая Советская Энциклопедия, 1973. (недоступная ссылка). Дата обращения: 25 апреля 2015. Архивировано 5 марта 2021 года.
- ↑ Горшков В. С. и др., Физическая химия силикатов, 1988, с. 193.
- ↑ Гамеева О. С., Физическая и коллоидная химия, 1969, с. 162.
- ↑ Физическая энциклопедия, т. 4, 1994, с. 196.
- ↑ Сивухин Д. В., Общий курс физики, т. 2, 2005, с. 42.
- ↑ Хаазе Р., Термодинамика необратимых процессов, 1967, с. 19.
- ↑ Münster A., Classical Thermodynamics, 1970, p. 20.
- ↑ Мюнстер А., Химическая термодинамика, 1971, с. 32.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 23.
- ↑ Хаазе Р., Термодинамика необратимых процессов, 1967, с. 25.
- ↑ Физическая энциклопедия, т. 3, 1992, с. 555.
- ↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, с. 11.
- ↑ Пригожин И., Кондепуди Д., Современная термодинамика, 2002, с. 52.
- ↑ Кубо Р., Термодинамика, 1970, с. 16.
- ↑ Магаев О. В. и др., Основы химической термодинамики, 2017, с. 8.
- ↑ Квасников И. А., Термодинамика, 2002, с. 22.
- ↑ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 66.
- ↑ Гуров К. П., Феноменологическая термодинамика необратимых процессов, 1978, с. 9.
- ↑ 59,0 59,1 Базаров И. П., Термодинамика, 2010, с. 21.
- ↑ 60,0 60,1 60,2 Базаров И. П., Термодинамика, 2010, с. 22.
- ↑ Мюнстер А., Химическая термодинамика, 1971, с. 15.
Литература
- Münster A. Classical Thermodynamics. — London e. a.: Wiley-Interscience, 1970. — xiv + 387 p. — ISBN 0 471 62430 6.
- Архаров А. М., Исаев С. И., Кожинов И. А. и др. Теплотехника / Под. общ. ред. В. И. Крутова. — М.: Машиностроение, 1986. — 432 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978–5–8114–1003–3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 112 с.
- Белонучкин В. Е. [libgen.io/book/index.php?md5=a2ce612148aa541d39a2f286713359b6 Краткий курс термодинамики]. — 2-е. — М.: МФТИ, 2010. — 164 с. — ISBN 978-5-7417-0337-3.
- Борщевский А. Я. [www.libgen.io/book/index.php?md5=A5B4FC1FCDA96540A34A61CBFEB2DD8D Физическая химия. Том 1 online. Общая и химическая термодинамика]. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4. (недоступная ссылка)
- Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с.
- Вукалович М. П., Новиков И. И. Термодинамика. — М.: Машиностроение, 1972. — 671 с.
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М.: Химия, 1970. — Т. I. — 592 с.
- Гамеева О. С. Физическая и коллоидная химия. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1969. — 408 с.
- Горшков В. С., Савельев В. Г., Федоров Н. Ф. Физическая химия силикатов и других тугоплавких соединений. — М.: Высшая школа, 1988. — 400 с. — ISBN 5-06-001389-8.
- Гуров К. П. Феноменологическая термодинамика необратимых процессов: Физические основы. — М.: Наука, 1978. — 128 с.
- Гухман А. А. Об основаниях термодинамики. — 2-е изд., испр. — М.: Изд-во ЛКИ, 2010. — 384 с. — ISBN 978-5-382-01105-9.
- Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
- Квасников И. А. Термодинамика и статистическая физика. — 2-е изд. — М.: Едиториал УРСС, 2002. — Т. 1. Термодинамика. — 238 с. — ISBN 5-354-00077-7.
- Козлов В. В.,. Ансамбли Гиббса и неравновесная статистическая механика. — М.: НИЦ «Регулярная и хаотическая динамика»; Ижевск: Институт компьютерных исследований, 2008. — 205 с. — ISBN 978-5-93972-645-0.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Куприков М. Ю. Реактивный двигатель // Большая российская энциклопедия. — Большая Российская энциклопедия, 2015. — Т. 28.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — 5-е изд. — М.: Физматлит, 2002. — 616 с. — (Теоретическая физика в 10 томах. Том 5). — ISBN 5-9221-0054-8.
- Магаев О. В., Минакова Т. С., Цыро Л. В. Основы химической термодинамики. — Томск: ИД Томск. гос. ун-та, 2017. — 208 с. — ISBN 978-5-94621-652-4.
- Мюнстер А. Химическая термодинамика. — М.: Мир, 1971. — 296 с.
- Новиков И. И. Термодинамика. — М.: Машиностроение, 1984. — 592 с.
- Петров Н., Бранков Й. Современные проблемы термодинамики. — Пер. с болг. — М.: Мир, 1986. — 287 с.
- Полянин А. Д., Полянин В. Д., Попов В. А. и др. Краткий справочник для инженеров и студентов. — М.: Международная программа образования, 1996. — 432 с. — ISBN 5-7753-0001-7.
- Поулз Д. Отрицательные абсолютные температуры и температуры во вращающихся системах координат // Успехи физических наук. — 1964. — Т. 84, № 4. — С. 693—713.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур / Пер. с англ. — М.: Мир, 2002. — 461 с. — (Лучший зарубежный учебник). — ISBN 5-03-003538-9.
- Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
- Сивухин Д. В. Общий курс физики. Т. II. Термодинамика и молекулярная физика. — 5-е изд., испр. — М.: Физматлит, 2005. — 544 с. — ISBN 5-9221-0601-5.
- Скаков С. В. Техническая термодинамика. — Липецк: [[Липецкий государственный
технический университет|ЛГТУ]], 2014. — 113 с. — ISBN 978-5-88247-698-3.
- Сторонкин А. В. Термодинамика гетерогенных систем. Части 1 и 2. — М.: Изд-во Ленингр. ун-та, 1967. — 448 с.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп.. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
- Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
- [www.libgen.io/book/index.php?md5=F0DD1E2241DFA869DADAFFD4614905AC Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин] / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с. (недоступная ссылка)
- Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — 672 с. — ISBN 5-85270-019-3.
- Хаазе Р.[нем.]. Термодинамика необратимых процессов / Пер. с нем. под ред. А. В. Лыкова. — М.: Мир, 1967. — 544 с.
- Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
- Хейвуд Р. Термодинамика равновесных процессов. Руководство для инженеров и научных работников. — М.: Мир, 1983. — 493 с.
- Черноуцан А. И. Краткий курс физики. — М.: Физматлит, 2002. — 320 с. — ISBN 5-9921-0292-3.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — 704 с. — ISBN 5-85270-087-8.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — 760 с. — ISBN 5-85270-101-7.
- Франк-Каменецкий Д. А. [www.libgen.io/book/index.php?md5=1A435B147BD48B0E7B10BD3C75BE7543 Лекции по физике плазмы]. — 2-е. — М.: Атомиздат, 1968. — 287 с. (недоступная ссылка)
- Эткинс П., де Паула Дж. Физическая химия. В 3-х частях. Часть 1. Равновесная термодинамика. — М.: Мир, 2007. — 495 с. — (Лучший зарубежный учебник). — ISBN 5-03-003786-1.


