Квадратура круга

Круг и квадрат одинаковой площади

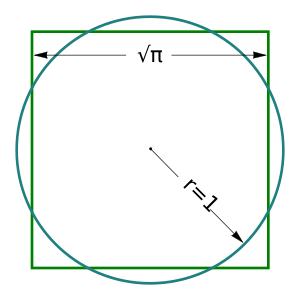
Квадрату́ра кру́га — задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки (без шкалы с делениями) квадрата, равновеликого по площади данному кругу. Наряду с трисекцией угла и удвоением куба, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

Если обозначить [math]\displaystyle{ R }[/math] радиус заданного круга, [math]\displaystyle{ x }[/math] — длину стороны искомого квадрата, то, в современном понимании, задача сводится к решению уравнения: [math]\displaystyle{ x^2 = \pi R^2, }[/math] откуда получаем: [math]\displaystyle{ x = \sqrt{\pi} R \approx 1{,}77245 R. }[/math] Доказано, что с помощью циркуля и линейки точно построить такую величину невозможно.

История

Из формулировки проблемы видно, что она тесно связана с практически важной задачей нахождения площади круга. В древнем Египте уже знали, что эта площадь [math]\displaystyle{ S }[/math] пропорциональна квадрату диаметра круга [math]\displaystyle{ d. }[/math] В папирусе Ринда для вычислений используется формула

[math]\displaystyle{ S = \left(\frac{8}{9}d\right)^2. }[/math]

Из этой формулы видно, что площадь круга диаметра [math]\displaystyle{ d }[/math] считалась равной площади квадрата со стороной [math]\displaystyle{ \frac{8}{9} d. }[/math] В современной терминологии это значит, что египтяне принимали значение [math]\displaystyle{ \pi }[/math] равным [math]\displaystyle{ \left(\frac{16}{9}\right)^2 \approx 3{,}16. }[/math]

Древнегреческие математики своей задачей считали не вычисление, а точное построение искомого квадрата («квадратуру»), причём, в соответствии с тогдашними принципами, только с помощью циркуля и линейки. Проблемой занимались крупнейшие античные учёные — Анаксагор, Антифонт, Брисон Гераклейский, Архимед, Спор и другие.

Гиппократ Хиосский в IV веке до н. э. первым обнаружил, что некоторые криволинейные фигуры (гиппократовы луночки) допускают точную квадратуру. Расширить класс таких фигур античным математикам не удалось. По другому пути пошёл его современник Динострат, показавший, что квадратуру круга можно строго выполнить с помощью особой кривой — квадратрисы.

В «Началах» Евклида (III век до н. э.) вопрос о площади круга не затрагивается. Важным этапом в исследовании проблемы стало сочинение Архимеда «Измерение круга», в котором впервые строго доказана теорема: площадь круга равна площади прямоугольного треугольника, у которого один катет равен радиусу круга, а другой — длине окружности. Это означало, что если удастся осуществить «спрямление окружности», то есть построить отрезок такой же длины, то проблема будет полностью решена. Архимед также дал оценку числа [math]\displaystyle{ \pi }[/math]:

[math]\displaystyle{ \frac{223}{71} \lt \pi \lt \frac{22}{7};\quad }[/math] в десятичной записи: [math]\displaystyle{ 3{,}1408 \lt \pi \lt 3{,}1429. }[/math]

Дальнейшие исследования индийских, исламских и европейских математиков по этой теме долгое время касались в основном уточнения значения числа [math]\displaystyle{ \pi }[/math] и подбора приближённых формул для квадратуры круга. В средневековой Европе задачей занимались Фибоначчи, Николай Кузанский и Леонардо да Винчи. Позднее обширные исследования опубликовали Кеплер и Гюйгенс. Постепенно укреплялась уверенность в том, что число [math]\displaystyle{ \pi }[/math] не может быть точно выражено с помощью конечного числа арифметических операций (включая извлечение корня), отсюда вытекала бы невозможность квадратуры круга. В 1775 году Парижская академия наук (за которой последовал ряд других академий мира) постановила не принимать к рассмотрению попытки квадратуры круга и прочих неразрешимых задач.

Иррациональность числа [math]\displaystyle{ \pi }[/math] была доказана Ламбертом в 1766 году в работе «Предварительные сведения для ищущих квадратуру и спрямление круга». Труд Ламберта содержал пробелы, вскоре исправленные Лежандром (1794 год). Окончательное доказательство неразрешимости квадратуры круга дал в 1882 году Линдеман (см. следующий раздел). Математики также предложили множество практически полезных способов приближённой квадратуры круга с хорошей точностью.

Неразрешимость

Если принять за единицу измерения радиус круга и обозначить x длину стороны искомого квадрата, то задача сводится к решению уравнения: [math]\displaystyle{ x^2=\pi }[/math], откуда: [math]\displaystyle{ x=\sqrt{\pi} }[/math]. С помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины [math]\displaystyle{ \pi }[/math]. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа [math]\displaystyle{ \pi }[/math], которая была доказана в 1882 году Линдеманом.

Однако эту неразрешимость следует понимать как неразрешимость при использовании только циркуля и линейки. Задача о квадратуре круга становится разрешимой, если, кроме циркуля и линейки, использовать другие средства (например, квадратрису). Простейший механический способ предложил Леонардо да Винчи. Изготовим круговой цилиндр с радиусом основания [math]\displaystyle{ R }[/math] и высотой [math]\displaystyle{ \frac{R}{2} }[/math], намажем чернилами боковую поверхность этого цилиндра и прокатим его по плоскости. За один полный оборот цилиндр отпечатает на плоскости прямоугольник площадью [math]\displaystyle{ \pi R^2 }[/math]. Располагая таким прямоугольником, уже несложно построить равновеликий ему квадрат.

Из теоремы Линдемана также следует, что осуществить квадратуру круга нельзя не только циркулем и линейкой, то есть с помощью прямых и окружностей, но и с помощью любых других алгебраических кривых и поверхностей (например, эллипсов, гипербол, кубических парабол и т. п.).

Приближённое решение

Пусть [math]\displaystyle{ a }[/math] — сторона квадрата, [math]\displaystyle{ D }[/math] — диагональ квадрата, [math]\displaystyle{ r }[/math] — радиус круга. Равенство площадей квадрата и круга: [math]\displaystyle{ \pi r^2 = a^2 }[/math]. По теореме Пифагора [math]\displaystyle{ D^2 = a^2 + a^2 }[/math], откуда [math]\displaystyle{ D = a \sqrt{2} }[/math], [math]\displaystyle{ a = \frac{D}{\sqrt{2}} }[/math]. Подставив [math]\displaystyle{ a }[/math] в равенство, получим [math]\displaystyle{ \pi r^2 = \left( \frac{D}{\sqrt{2}} \right)^2 }[/math]. Выразив [math]\displaystyle{ D }[/math], получим [math]\displaystyle{ D = r \sqrt{2 \pi} \approx 2{,}506628275 \cdot r }[/math]. Диагональ искомого квадрата приближённо равна 2,5 радиусам круга. Построив квадрат со стороной указанной длины и взяв половину его диагонали, получим сторону искомого приближённого квадрата. При данном построении погрешность составит 0,016592653. При исходном радиусе в 1 метр вы получите «недостачу по площади» в размере чуть более 10 спичечных коробков.

Метафора «квадратура круга»

Математическое доказательство невозможности квадратуры круга не мешало многим энтузиастам тратить годы на решение этой проблемы. Тщетность исследований по решению задачи квадратуры круга перенесла этот оборот во многие другие области, где он попросту обозначает безнадёжное, бессмысленное или тщетное предприятие. См. также вечный двигатель.

См. также

• Квадратриса
• Построение с помощью циркуля и линейки
• Трисекция угла
• Удвоение куба
• Квадратура круга Тарского

Литература

• Белозеров С. Е. Пять знаменитых задач древности. История и современная теория. — Ростов: изд-во Ростовского университета, 1975. — 320 с.
• Манин Ю. И. О разрешимости задач на построение с помощью циркуля и линейки. Энциклопедия элементарной математики. Книга четвёртая (геометрия) Архивная копия от 18 сентября 2011 на Wayback Machine, М., Физматгиз, 1963. — 568 с.
• Перельман Я. И. Квадратура круга. Л.: Дом занимательной науки, 1941.
• Прасолов В. В.. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. Архивная копия от 9 декабря 2008 на Wayback Machine М.: Наука, 1992. 80 с. Серия «Популярные лекции по математике», выпуск 62.
• Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.—Л.: ОГИЗ, 1936. — 237 с. — (Классики естествознания).
• Хал Хеллман. Великие противостояния в науке. Десять самых захватывающих диспутов. Глава 2. Валлис против Гоббса: Квадратура круга = Great Feuds in Science: Ten of the Liveliest Disputes Ever. — М.: «Диалектика», 2007. — 320 с. — ISBN 0-471-35066-4.
• Чистяков В. Д. Три знаменитые задачи древности. — М.: Гос. уч.-пед. изд-во Министерства просвещения РСФСР, 1963. — 96 с..
• Щетников А. И. Как были найдены некоторые решения трёх классических задач древности? // Математическое образование. — 2008. — № 4 (48). — С. 3—15.