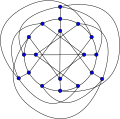
Граф Робертсона

Граф Робертсона
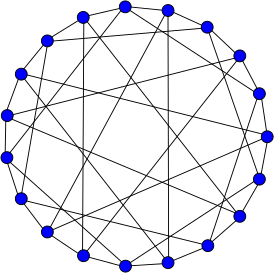Граф Робертсона гамильтонов
Назван в честь	Нейла Робертсона
Вершин	19
Рёбер	38
Диаметр	3
Обхват	5
Автоморфизмы	24 (D12)
Хроматическое число	3
Хроматический индекс	5
Свойства	Клетка Гамильтонов
Книжная толщина	3
Число очередей	2

Граф Робертсона или (4,5)-клетка — это 4-регулярный неориентированный граф с 19 вершинами и 38 рёбрами, названный именем Нейла Робертсона.

Граф Робертсона является уникальной (4,5)-клеткой и его открыл Робертсон в 1964 году. Как клетка, граф является наименьшим 4-регулярным графом с обхватом 5.

Граф имеет хроматическое число 3, хроматический индекс 5, диаметр 3, радиус 3, он вершинно 4-связен и рёберно 4-связен. Его книжная толщина равна 3 и число очередей равно 2.

Граф Робертсона гамильтонов и он имеет 5376 различных гамильтоновых циклов.

Алгебраические свойства

Граф Робертсона не вершинно-транзитивен и его полная группа автоморфизмов изоморфна диэдральной группе порядка 24, группе симметрий правильного двенадцатиугольника, включая как вращения, так и отражения.

Характеристический многочлен графа Робертсона равен

[math]\displaystyle{ (x-4)(x-1)^2(x^2-3)^2(x^2+x-5) }[/math]

[math]\displaystyle{ (x^2+x-4)^2(x^2+x-3)^2(x^2+x-1).\ }[/math]

Галерея

• 

  Граф Робертсона как он был изображён в оригинальной публикации.

• 

  Хроматическое число графа Робертсона равно 3.

• 

  Хроматический индекс графа Робертсона равен 5.

Ссылки

• M₂₂ graph Архивная копия от 18 февраля 2019 на Wayback Machine at MathWorld