Параболоид
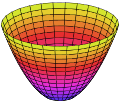


Параболо́ид ― тип поверхности второго порядка в трёхмерном евклидовом пространстве.
Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.
Канонические уравнения параболоида в декартовых координатах:
- [math]\displaystyle{ z= tx^2+uy^2, }[/math]
- где [math]\displaystyle{ t }[/math] и [math]\displaystyle{ u }[/math] — действительные числа, не равные нулю одновременно.
При этом:
- если [math]\displaystyle{ t }[/math] и [math]\displaystyle{ u }[/math] одного знака, то параболоид называется эллиптическим, частный случай эллиптического параболоида [math]\displaystyle{ t = u, }[/math] в этом случае поверхность принято называть параболоидом вращения;
- если [math]\displaystyle{ t }[/math] и [math]\displaystyle{ u }[/math] разного знака, то параболоид называется гиперболическим;
- если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.
Cечения параболоида вертикальными (параллельными оси [math]\displaystyle{ z }[/math]) плоскостями произвольного положения — параболы.
Сечения параболоида горизонтальными плоскостями, параллельными плоскости [math]\displaystyle{ x,\ y }[/math] для эллиптического параболоида — эллипсы, для параболоида вращения эти пересечения — окружности, когда такое пересечение существует.
Пересечения для гиперболического параболоида — гиперболы.
В частных случаях пересечения, сечением может оказаться прямая или пара прямых (для гиперболического параболоида или пара параллельных прямых для параболического цилиндра) или вырождаться в одну точку (для эллиптического параболоида).
Эллиптический параболоид
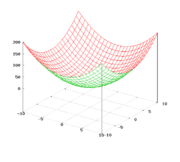
Эллипти́ческий параболо́ид — поверхность, задаваемая функцией вида:
- [math]\displaystyle{ z = \frac {x^2}{a^2} + \frac {y^2}{b^2}. }[/math]
Эллиптический параболоид можно описать как семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх (см. рисунок).
Если [math]\displaystyle{ a=b }[/math], то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг её оси симметрии.
Гиперболический параболоид
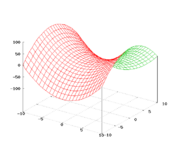
Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седловая поверхность, описываемая в прямоугольной системе координат уравнением вида
- [math]\displaystyle{ z = \frac {x^2}{a^2} - \frac {y^2}{b^2} }[/math] или [math]\displaystyle{ z = \frac {y^2}{b^2} - \frac {x^2}{a^2}. }[/math]
Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх (см. рисунок).

Гиперболический параболоид является линейчатой поверхностью.
Поверхность, порождаемая билинейной интерполяцией некоторой функции по 4 точкам, является гиперболическим параболоидом.
Интересные факты
- Поверхность жидкости в равномерно вращающемся сосуде является параболоидом вращения (что не является прямой причиной его названия).
- Часто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основана работа параболических антенн, телескопов-рефлекторов с параболическим зеркалом, прожекторов, автомобильных фар и т. д. Подробнее, см. рефлектор (зеркало).
См. также
- Гиперболоид — другой вид поверхности второго порядка.
- Поверхности второго порядка.
- Квадратичная форма.
Литература
- Делоне Б. Н., Райков Д. А. Аналитическая геометрия, в двух томах. — М., Л.: Гостехиздат, 1948, 1949.
- Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
- Канатников А. Н., Крищенко А. П. Аналитическая геометрия. — М.: Издательство МГТУ им. Н. Э. Баумана, 2002. — 388 с. — ISBN 5-7038-1671-8.
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |