Бикасательные плоской кривой четвёртой степени

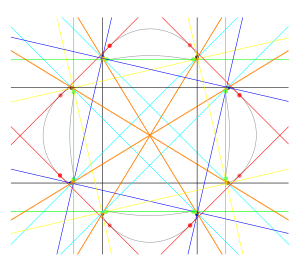
Плоская кривая четвёртой степени общего вида имеет 28 бикасательных, то есть прямых, касающихся кривой в двух точках. Эти прямые существуют в комплексной проективной плоскости, но можно найти кривые, для которых все 28 из этих прямых имеют вещественные числа в качестве координат, а потому принадлежит евклидовой плоскости.
Явные кривые четвёртого порядка с двадцатью восемью вещественными бикасательными первым нашёл Юлиус Плюккер[1][2]. Как показал Плюккер, число вещественных бикасательных любой кривой четвёртого порядка должно быть равно 28, 16 или должно быть меньше 9. Другую кривую четвёртого порядка с 28 вещественными бикасательными можно образовать как геометрическое место точек центров эллипсов с фиксированными длинами осей, касающихся двух непараллельных прямых[3]. Шиода[4] дал другое построение кривых четвёртого порядка с двадцатью восемью бикасательными, которая образуется проекцией кубической поверхности. Двадцать семь бикасательных кривой Шиода вещественны, а двадцать восьмая является бесконечно удалённой прямой[англ.] в проективной плоскости.
Пример
Кривая Тротта, другая кривая с 28 вещественными бикасательными, является множеством точек (x,y), удовлетворяющих уравнению четвёртой степени
- [math]\displaystyle{ \displaystyle 144(x^4+y^4)-225(x^2+y^2)+350x^2y^2+81=0. }[/math]
Эти точки образуют несингулярную кривую четвёртого порядка, имеющую род три и двадцать восемь вещественных бикасательных[5].
Подобно примеру Плюкера и кривой Блюма и Гуинанда, кривая Тротта имеет четыре раздельных (неправильных) овала, максимальное число для кривых четвёртого порядка, а потому является M-кривой. Четыре овала можно сгруппировать в шесть различных пар овалов. Для каждой пары овалов имеется четыре бикасательных, касающихся обоих овалов в паре, две прямые разделяют овалы и две не разделяют. Кроме того, каждый овал ограничивает невыпуклую область плоскости и имеет одну бикасательную, связывающую невыпуклые порции границы.
Связь с другими структурами
Двойственная кривая (первичной) кривой четвёртого порядка имеет 28 вещественных обыкновенных двойных точек, двойственных 28 бикасательным первичной кривой.
28 бикасательных кривой четвёртого порядка могут быть сопоставлены символам вида
- [math]\displaystyle{ \left[ \begin{array}{ccc}a&b&c\\d&e&f\\ \end{array}\right] }[/math]
где a, b, c, d, e и f равны нулю или единице и для них выполняется
Существует 64 комплекта a, b, c, d, e и f, но только 28 из них дают нечётную сумму. Можно интерпретировать a, b и c как однородные координаты точки плоскости Фано, а d, e и f как координаты прямой в той же конечной проективной плоскости. Условие нечётности суммы эквивалентно требованию, что точка не лежит на прямой, и существует 28 различных пар таких точек и прямых.
Точки и прямые плоскости Фано, образующие неинцидентные пары, образуют треугольник, и бикасательные кривой четвёртого порядка можно рассматривать как соответствующие 28 треугольникам плоскости Фано[8]. Графом Леви плоскости Фано служит граф Хивуда, в котором треугольники плоскости Фано представлены 6-циклами. 28 6-циклов графа Хивуда, в свою очередь, соответствуют 28 вершинам графа Коксетера[9].
28 бикасательных кривой четвёртого порядка также соответствуют 56 парам прямых поверхности дель Пеццо[англ.] степени 2[8] и 28 нечётным тэта-характеристикам[англ.].
27 прямых кривой третьего порядка и 28 бикасательных кривой четвёртого порядка, вместе со 120 трикасательными плоскостями канонической кривой шестого порядка рода 4 образуют «„троицу“» Арнольда, точнее, образуют соответствие Маккея[англ.][10][11][12] и могут быть связаны с многими другими объектами, включая E7 и E8, как обсуждается в статье «ADE-классификация».
Примечания
- ↑ Plücker, 1839.
- ↑ Gray, 1982.
- ↑ Blum, Guinand, 1964.
- ↑ Shioda, 1995.
- ↑ Trott, 1997.
- ↑ Riemann, 1876.
- ↑ Cayley, 1879.
- ↑ 8,0 8,1 Manivel, 2006.
- ↑ Dejter, 2011.
- ↑ le Bruyn, 2008.
- ↑ Arnold, 1997, с. 13.
- ↑ McKay, Sebbar, 2007, с. 11.
Литература
- Blum R., Guinand A. P. A quartic with 28 real bitangents // Canadian Mathematical Bulletin. — 1964. — Т. 7. — С. 399–404. — doi:10.4153/cmb-1964-038-6.
- Arthur Cayley. On the bitangents of a quartic // Salmon's Higher Plane Curves. — 1879. — С. 387–389.. В книге The collected mathematical papers of Arthur Cayley, Andrew Russell Forsyth, ed., The University Press, 1896, vol. 11, pp. 221—223.
- Jeremy Gray. From the history of a simple group // The Mathematical Intelligencer. — 1982. — Т. 4, вып. 2. — С. 59–67. — doi:10.1007/BF03023483.
- The Eightfold Way / Silvio Levy. — Cambridge University Press, 1999. — Т. 35. — С. 115–131. — (MSRI Publications). — ISBN 0-521-66066-1.
- Manive L. Configurations of lines and models of Lie algebras // Journal of Algebra. — 2006. — Т. 304, вып. 1. — С. 457–486. — doi:10.1016/j.jalgebra.2006.04.029.
- Julius Plücker. Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie. — Berlin: Adolph Marcus, 1839.
- Manivel L. Configurations of lines and models of Lie algebras // Journal of Algebra. — 2006. — Т. 304, вып. 1. — С. 457–486. — doi:10.1016/j.jalgebra.2006.04.029.
- Riemann G. F. B. Zur Theorie der Abel'schen Funktionen für den Fall p = 3 // Ges. Werke. — Leipzig, 1876. — С. 456–472.. Как цитировано у Кэли.
- Tetsuji Shioda. Weierstrass transformations and cubic surfaces // Commentarii Mathematici Universitatis Sancti Pauli. — 1995. — Т. 44, вып. 1. — С. 109–128.
- Michael Trott. Applying GroebnerBasis to Three Problems in Geometry // Mathematica in Education and Research. — 1997. — Т. 6, вып. 1. — С. 15–28.
- Italo J. Dejter. From the Coxeter graph to the Klein graph // Journal of Graph Theory. — 2011. — doi:10.1002/jgt.20597. — arXiv:1002.1960.
- Lieven le Bruyn. Arnold’s trinities. — 2008. — Июнь. Архивировано 11 апреля 2011 года.
- Vladimir Arnold. 1997, Toronto Lectures, Lecture 2: Symplectization, Complexification and Mathematical Trinities. — 1997. — С. 13. TeX, PostScript, Онлайн-письма Арнольда
- Italo J. Dejter. From the Coxeter graph to the Klein graph // Journal of Graph Theory. — 2011. — doi:10.1002/jgt.20597. — arXiv:1002.1960.
- McKay J., Sebbar A. Replicable Functions: An introduction // Frontiers in Number Theory, Physics, and Geometry, II. — Springer, 2007. — С. 373–386. — doi:10.1007/978-3-540-30308-4_10.