Фактор-критический граф

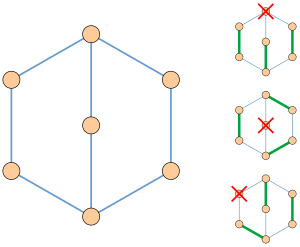
Фактор-критический граф вместе с наибольшими паросочетаниями подграфов, полученных удалением одной из вершин.

Фактор-критический граф (или почти сочетаемый граф .) — это граф с n вершинами, в котором каждый подграф с n − 1 вершинами имеет совершенное паросочетание. (Совершенное паросочетание в графе — это подмножество рёбер со свойством, что каждая из вершин графа является конечной вершиной в точности одного ребра из подмножества.)

Сочетание, покрывающее все вершины, кроме одной, называется почти совершенным паросочетанием. Таким образом, эквивалентно, фактор-критический граф — это граф, в котором существуют почти совершенные паросочетания, которые не содержат любую из вершин.

Примеры

Три графа дружеских отношений, примеры негамильтоновых фактор-критических графов

Cкрученно удлинённая пятиугольная пирамида, фактор-критический граф без клешней

Любой цикл нечётной длины является фактор-критическим, как и любой полный граф с нечётным числом вершин. Более обще, любой гамильтонов граф с нечётным числом вершин является фактор-критическим. Графы дружеских отношений (графы, образованные соединением набора треугольников с одной общей вершиной) дают примеры графов, фактор-критических, но не гамильтоновых.

Если граф G является фактор-критическим, то он является мычельскианом графа G. Например, граф Грёча, мычельскиан цикла с пятью вершинами, является фактор-критическим.

Любой вершинно 2-связный граф без клешней с нечётным числом вершин является фактор-критическим. Например, граф с 11 вершинами, образованный вершинами правильного икосаэдра (граф скрученно удлинённой пятиугольной пирамиды), является как 2-связным, так и свободным от клешней, так что он является фактор-критическим. Этот результат следует прямо из более фундаментальной теоремы, что любой связный граф без клешней с чётным числом вершин имеет совершенное паросочетание.

Описание

Фактор-критические графы можно описать несколькими различными путями, отличными от определения как графы, удаление любой вершины которых позволяет совершенное паросочетание:

• Тибор Галлаи доказал, что граф является фактор-критическим тогда и только тогда, когда он связен и для любой вершины v графа, существует наибольшее паросочетание, которое не включает v. Из этого свойства следует, что граф должен иметь нечётное число вершин и что любое наибольшее паросочетание должно включать все, кроме одной вершины.
• Ласло Ловас доказал, что граф является фактор-критическим тогда и только тогда, когда он имеет нечётную ушную декомпозицию, разбиение рёбер на последовательность подграфов, каждый из которых является путём или циклом нечётной длины, и первый подграф в последовательности является циклом, каждый путь в последовательности имеет конечные, но не внутренние, вершины на предыдущих подграфах, а каждый цикл, отличный от первого, имеет ровно одну вершину, общую с предыдущими подграфами. Например, граф на иллюстрации может быть разбит этим образом на циклы с пятью рёбрами и пути с тремя рёбрами. В случае, когда почти совершенное паросочетание фактор-критического графа также задано, ушное разложение может быть выбрано таким образом, что каждое ухо попеременно проходит рёбра паросочетания и рёбра, не входящие в паросочетание.
• Граф является также фактор-критическим тогда и только тогда, когда его можно свести к графу с единственной вершиной путём стягивания циклов нечётной длины. Более того, в этом случае можно выбрать каждый цикл в последовательности таким образом, чтобы он содержал вершину, полученную стягиванием предыдущего цикла. Например, если стягивать уши ушного разложения в порядке, заданном разложением, то каждый раз стягиваемое ухо образует нечётный цикл, так что описание с помощью ушного разложения можно использовать для поиска последовательности нечётных циклов для стягивания. Обратно, из последовательности стягиваний нечётных циклов, содержащих вершины, полученные на предыдущих стягиваниях, можно образовать ушное разложение, в котором уши образуют множества стягиваемых рёбер.
• Предположим, что граф G задан вместе с выбранной вершиной v и паросочетанием M, покрывающим все вершины, отличные от v. Тогда G является фактор-критическим тогда и только тогда, когда существует множество путей в G, состоящих из поочерёдно идущих рёбер из паросочетаний и рёбер, не входящих в паросочетание, соединяющих вершину v со всеми остальными вершинами графа G. Основываясь на этом свойстве, можно определить за линейное время, является ли граф G с заданным почти совершенным паросочетанием фактор-критическим.

Свойства

Фактор-критические графы должны всегда иметь нечётное число вершин и должны быть рёберно 2-связными (то есть они не могут иметь какого-либо моста). Однако они не обязательно вершинно 2-связны. Графы дружеских отношений дают контрпример. Фактор-критический граф не может быть двудольным, поскольку в двудольном графе с почти совершенным паросочетанием только вершины, которые могут быть удалены для получения графа с совершенным паросочетанием, находятся на большей стороне двудольного графа.

Любой вершинно 2-связный фактор-критический граф с m рёбрами имеет по меньшей мере m различных почти совершенных паросочетаний, и, более обще, любой фактор-критический граф с m рёбрами и c блоками (связных компонент из 2 вершин) имеет по меньшей мере m − c + 1 различных почти совершенных паросочетаний. Графы, для которых эти границы точны, можно описать как имеющие ушное разложение специфичного вида.

Любой связный граф можно преобразовать в фактор-критический граф путём стягивания достаточно много рёбер. Минимальный набор рёбер, которые нужно стянуть, чтобы сделать заданный граф G фактор-критическим, образует базис матроида, факт, из которого следует, что работающий за полиномиальное время жадный алгоритм может быть использован для поиска наименьшего взвешенного множества рёбер, стягивание которых делает граф фактор-критическим. Ранний алгоритм стягивания минимального числа (невзвешенных) рёбер для получения фактор-критического графа можно найти в статье Франка.

Приложения

Цветок — это фактор-критический подграф большего графа. Цветки играют ключевую роль в алгоритмах Эдмондса поиска наибольшего паросочетания и минимального взвешенного совершенного сочетания в недвудольных графах.

В комбинаторике многогранников фактор-критические графы играют важную роль при описании фасет многогранников паросочетаний заданного графа.

Обобщения и связанные концепции

Говорят, что граф k-фактор критический, если любое подмножество из n − k вершин имеет совершенное паросочетание. При таком определении почти сочетаемый (en:hypomatchable) граф является 1-фактор-критическим. Даже более обще, граф является (a,b)-фактор-критическим, если любое подмножество из n − k вершин имеет r-фактор, то есть он является набором вершин r-регулярного подграфа заданного графа.

Когда говорят о критическом графе (без уточнения k-), обычно имеют в виду граф, удаление любой вершины которого приводит к уменьшению числа цветов, необходимых для раскраски графа. Понятие критичности используется значительно шире в теории графов для графов, в которых удаление любой вершины изменяет какое-то свойство графа. Критичный по сочетаниям граф — это граф, для которого удаление любой вершины не изменяет размера наибольшего паросочетания. Согласно Галлаи, критичные по сочетаниям графы, это в точности графы, в которых любая связная компонента является фактор-критической. Дополнение критического графа обязательно критично по сочетаниям, факт, который использовал Галлаи для доказательства нижней границы числа вершин критического графа.

Вне теории графов понятие фактор-критичности имеет расширение на матроиды путём определения типа ушного разложения на матроидах. Матроид является фактор-критическим, если он имеет ушное разложение, в котором все уши нечётные.