Теория изгиба балок Тимошенко

Теория изгиба балок Тимошенко была развита Степаном Прокофьевичем Тимошенко в начале XX века.^[1]^[2] Модель учитывает сдвиговую деформацию и вращательные изгибы, что делает её применимой для описания поведения толстых балок, сэндвич-панелей и высокочастотных колебаний балок, когда длина волны этих колебаний становится сравнимой с толщиной балки. В отличие от модели изгиба балок Эйлера-Бернулли модель Тимошенко приводит к уравнению четвертого порядка, которое также содержит и частные производные второго порядка. Физически учёт механизмов деформации эффективно снижает жёсткость балки и приводит к большему отклонению при статической нагрузке и к предсказанию меньших собственных частот для заданного набора граничных условий. Последнее следствие наиболее заметно для высоких частот, поскольку длина волны колебаний становится короче и расстояние между противоположно направленными сдвиговыми силами уменьшается.

Если модуль сдвига материала балки положить равным бесконечности (и следовательно запретить балке испытывать сдвиговые деформации) и если пренебречь эффектами инерции на вращение, то модель Тимошенко сводится к обычной теории изгиба балки.

Квазистатическая балка Тимошенко

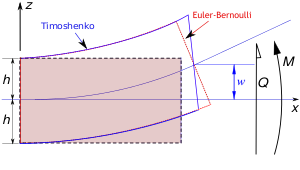
Сравнение деформации балки по Тимошенко (синий цвет) с деформацией по теории Эйлера-Бернулли (красный цвет).

В статической теории балки Тимошенко без осевых эффектов смещение балки предполагается заданным в следующем виде: [math]\displaystyle{ u_x(x,y,z) = -z~\varphi(x) ~;~~ u_y(x,y,z) = 0 ~;~~ u_z(x,y) = w(x) }[/math] где [math]\displaystyle{ (x,y,z) }[/math] задают координаты точки на балке, [math]\displaystyle{ u_x, u_y, u_z }[/math] — компоненты вектора смещения в трех координатных направлениях, [math]\displaystyle{ \varphi }[/math] — есть угол вращения нормали по отношению срединной поверхности балки и [math]\displaystyle{ w }[/math] — смещение срединной поверхности в направлении оси [math]\displaystyle{ z }[/math].

Исходными уравнениями является следующая пара связанных обыкновенных дифференциальных уравнений:

[math]\displaystyle{ \begin{align} & \frac{\mathrm{d}^2}{\mathrm{d} x^2}\left(EI\frac{\mathrm{d} \varphi}{\mathrm{d} x}\right) = q(x) \\ & \frac{\mathrm{d} w}{\mathrm{d} x} = \varphi - \frac{1}{\kappa AG} \frac{\mathrm{d}}{\mathrm{d} x}\left(EI\frac{\mathrm{d} \varphi}{\mathrm{d} x}\right). \end{align} }[/math]

В статическом пределе теория изгиба балки Тимошенко эквивалентна теории изгиба балок Эйлера-Бернулли в случае, когда последним слагаемым можно пренебречь. Это приближение справедливо когда: [math]\displaystyle{ \frac{EI}{\kappa L^2 A G} \ll 1 }[/math] где

[math]\displaystyle{ L }[/math] — длина балки.
[math]\displaystyle{ A }[/math] — площадь сечения балки.
[math]\displaystyle{ E }[/math] — модуль упругости.
[math]\displaystyle{ G }[/math] — модуль сдвига.
[math]\displaystyle{ I }[/math] — второй момент площади сечения.
[math]\displaystyle{ \kappa }[/math] называется сдвиговым коэффициентом Тимошенко и зависит от формы сечения балки. Для балки прямоугольного сечения [math]\displaystyle{ \kappa = 5/6 }[/math].
[math]\displaystyle{ q(x) }[/math] — распределение нагрузки (сила приложенная к единице длины).

Комбинируя эти два уравнения получаем в случае однородной балки постоянного сечения: [math]\displaystyle{ EI~\cfrac{\mathrm{d}^4 w}{\mathrm{d} x^4} = q(x) - \cfrac{EI}{\kappa A G}~\cfrac{\mathrm{d}^2 q}{\mathrm{d} x^2} }[/math]

Изгибающий момент [math]\displaystyle{ M_{xx} }[/math] и сдвиговая сила [math]\displaystyle{ Q_x }[/math] в балке связаны со смещением [math]\displaystyle{ w }[/math] и вращением [math]\displaystyle{ \varphi }[/math]. В случае линейной упругой балки Тимошенко эти связи имеют следующий вид:

[math]\displaystyle{ M_{xx} = -EI~\frac{\partial \varphi}{\partial x} \quad \text{и} \quad Q_{x} = \kappa~AG~\left(-\varphi + \frac{\partial w}{\partial x}\right) \,. }[/math]

Вывод квазистатических уравнений изгиба балок по Тимошенко

Из кинематических предположений для балки Тимошенко смещение балки даётся:

[math]\displaystyle{ u_x(x,y,z,t) = -z~\varphi(x,t) ~;~~ u_y(x,y,z,t) = 0 ~;~~ u_z(x,y,z) = w(x,t) }[/math] Далее, в случае малых деформаций в рамках предположений Тимошенко можно написать: [math]\displaystyle{ \varepsilon_{xx} = \frac{\partial u_x}{\partial x} = -z~\frac{\partial \varphi}{\partial x} ~;~~ \varepsilon_{xz} = \frac{1}{2}\left(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x}\right) = \frac{1}{2}\left(-\varphi + \frac{\partial w}{\partial x}\right) }[/math] Поскольку реальные сдвиговые деформации балки непостоянны в пределах сечения, введём корректирующий фактор [math]\displaystyle{ \kappa }[/math] такой, что: [math]\displaystyle{ \varepsilon_{xz} = \frac{1}{2}~\kappa~\left(-\varphi + \frac{\partial w}{\partial x}\right) }[/math]

Изменение внутренней энергии балки можно записать в виде:

[math]\displaystyle{ \delta U = \int_L \int_A (\sigma_{xx}\delta\varepsilon_{xx} + 2\sigma_{xz}\delta\varepsilon_{xz})~\mathrm{d}A~\mathrm{d}L = \int_L \int_A \left[-z~\sigma_{xx}\frac{\partial (\delta\varphi)}{\partial x} + \sigma_{xz}~\kappa\left(-\delta\varphi + \frac{\partial (\delta w)}{\partial x}\right)\right]~\mathrm{d}A~\mathrm{d}L }[/math]

Зададим:

[math]\displaystyle{ M_{xx} := \int_A z~\sigma_{xx}~\mathrm{d}A ~;~~ Q_x := \kappa~\int_A \sigma_{xz}~\mathrm{d}A }[/math]

Тогда:

[math]\displaystyle{ \delta U = \int_L \left[-M_{xx}\frac{\partial (\delta\varphi)}{\partial x} + Q_{x}\left(-\delta\varphi + \frac{\partial (\delta w)}{\partial x}\right)\right]~\mathrm{d}L }[/math]

Интегрируя по частям и замечая, что граничные условия обращают изменение энергии на концах балки в нуль, пишем:

[math]\displaystyle{ \delta U = \int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \frac{\partial Q_{x}}{\partial x}~\delta w\right]~\mathrm{d}L }[/math]

Изменение внешней работы, совершенной над балкой поперечной нагрузкой [math]\displaystyle{ q(x,t) }[/math] на единицу длины, равно:

[math]\displaystyle{ \delta W = \int_L q~\delta w~\mathrm{d}L }[/math]

Тогда для квазистатичной балки принцип виртуальной работы дает:

[math]\displaystyle{ \delta U = \delta W \implies \int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} + q\right)~\delta w\right]~\mathrm{d}L = 0 }[/math]

Исходные уравнения для балки исходя из фундаментальной теоремы вариационного исчисления обретают вид:

[math]\displaystyle{ \frac{\partial M_{xx}}{\partial x} - Q_x = 0 ~;~~ \frac{\partial Q_{x}}{\partial x} + q = 0 }[/math]

Для линейной упругой балки:

[math]\displaystyle{ \begin{align} M_{xx} & = \int_A z~\sigma_{xx}~\mathrm{d}A = \int_A z~E~\varepsilon_{xx}~\mathrm{d}A = -\int_A z^2~E~\frac{\partial \varphi}{\partial x}~\mathrm{d}A = -EI~\frac{\partial \varphi}{\partial x} \\ Q_{x} & = \int_A \sigma_{xz}~\mathrm{d}A = \int_A 2G~\varepsilon_{xz}~\mathrm{d}A = \int_A \kappa~G~\left(-\varphi + \frac{\partial w}{\partial x}\right)~\mathrm{d}A = \kappa~AG~\left(-\varphi + \frac{\partial w}{\partial x}\right) \end{align} }[/math]

Следовательно, основные уравнения для балки могут быть записаны в виде:

[math]\displaystyle{ \begin{align} \frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) + \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\ \frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] + q & = 0 \end{align} }[/math]

Комбинируя вместе два уравнения, получаем:

[math]\displaystyle{ \begin{align} & \frac{\partial^2 }{\partial x^2}\left(EI\frac{\partial \varphi}{\partial x}\right) = q \\ & \frac{\partial w}{\partial x} = \varphi - \cfrac{1}{\kappa AG}~\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) \end{align} }[/math]

Краевые (граничные) условия

Два уравнения, которые описывают деформацию балки Тимошенко, должны быть дополнены краевыми (граничными) условиями. Корректно поставленная задача требует задания четырех граничных условий. Обычно граничными условиями являются:

Двухопорные балки: Смещение [math]\displaystyle{ w }[/math] задается равным нулю в местах расположения двух опор. Также нужно задать изгибающий момент [math]\displaystyle{ M_{xx} }[/math], приложенный к балке. Вращение [math]\displaystyle{ \varphi }[/math] и поперечная сдвиговая сила [math]\displaystyle{ Q_x }[/math] не заданы.
Жёстко защемлённая балка (консоль): Смещение [math]\displaystyle{ w }[/math] и вращение [math]\displaystyle{ \varphi }[/math] задаются равными нулю в месте защемленного конца балки. Если один из концов балки свободен, то сдвиговая сила [math]\displaystyle{ Q_x }[/math] и изгибающий момент [math]\displaystyle{ M_{xx} }[/math] необходимо задать для этого конца.

Пример: Жестко защемленная балка

Жестко защемленная балка Тимошенко со свободным концом при точечной нагрузке

Для жестко защемленной балки один конец защемлен, а другой остается свободным. Будем использовать правовинтовую систему координат, в которой направление оси [math]\displaystyle{ x }[/math] считается положительным в направлении вправо, а направление оси [math]\displaystyle{ z }[/math] положительно в направлении вверх. Следуя традиционным соглашениям мы предположим, что положительные значения сил направлены в положительном направлении осей [math]\displaystyle{ x }[/math] и [math]\displaystyle{ z }[/math], а положительные изгибающие моменты действуют по часовой стрелке. Также предположим следующее соглашение о знаках компонент механических напряжений ([math]\displaystyle{ M_{xx} }[/math] и [math]\displaystyle{ Q_x }[/math]): положительные изгибающие моменты сжимают материал балки внизу (меньшие значения координат [math]\displaystyle{ z }[/math]), положительные сдвиговые силы вращают балку против часовой стрелки.

Предположим, что защемленный конец балки имеет координату [math]\displaystyle{ x=L }[/math],а свободный конец — [math]\displaystyle{ x=0 }[/math]. Если точечная нагрузка [math]\displaystyle{ P }[/math] приложена к свободному концу в положительном направлении оси [math]\displaystyle{ z }[/math], то условие равновесия системы сходящихся сил балки дает нам

[math]\displaystyle{ -Px - M_{xx} = 0 \implies M_{xx} = -Px }[/math]

и

[math]\displaystyle{ P + Q_x = 0 \implies Q_x = -P\,. }[/math]

Следовательно, из выражений для изгибного момента и сдвиговой силы получаем

[math]\displaystyle{ Px = EI\,\frac{d\varphi}{dx} \qquad \text{и} \qquad -P = \kappa AG\left(-\varphi + \frac{dw}{dx}\right) \,. }[/math]

Интегрируя первое уравнение и применяя граничное условие [math]\displaystyle{ \varphi = 0 }[/math] при [math]\displaystyle{ x = L }[/math] приходим к

[math]\displaystyle{ \varphi(x) = -\frac{P}{2EI}\,(L^2-x^2) \,. }[/math]

Второе уравнение может быть переписано в виде

[math]\displaystyle{ \frac{dw}{dx} = -\frac{P}{\kappa AG} - \frac{P}{2EI}\,(L^2-x^2)\,. }[/math]

Интегрируя и применяя граничное условие [math]\displaystyle{ w = 0 }[/math] при [math]\displaystyle{ x = L }[/math] пишем

[math]\displaystyle{ w(x) = \frac{P(L-x)}{\kappa AG} - \frac{Px}{2EI}\,\left(L^2-\frac{x^2}{3}\right) + \frac{PL^3}{3EI} \,. }[/math]

Осевое напряжение дается тогда выражением

[math]\displaystyle{ \sigma_{xx}(x,z) = E\,\varepsilon_{xx} = -E\,z\,\frac{d\varphi}{dx} = -\frac{Pxz}{I} = \frac{M_{xx}z}{I} \,. }[/math]

Динамика балки Тимошенко

В теории изгиба балки Тимошенко без осевых эффектов отклонение балки предполагается заданным в виде

[math]\displaystyle{ u_x(x,y,z,t) = -z~\varphi(x,t) ~;~~ u_y(x,y,z,t) = 0 ~;~~ u_z(x,y,z,t) = w(x,t) }[/math]

где [math]\displaystyle{ (x,y,z) }[/math] — координаты точки балки, [math]\displaystyle{ u_x, u_y, u_z }[/math] — компоненты вектора отклонения в трех координатных направлениях, [math]\displaystyle{ \varphi }[/math] — угол вращения нормали по отношению к срединной поверхности балки и [math]\displaystyle{ w }[/math] — отклонение срединной поверхности в направлении оси [math]\displaystyle{ z }[/math].

Учитывая вышесказанное предположение теория изгиба балки Тимошенко (с допущением колебаний) может быть описано парой линейных уравнений в частных производных:^[3]

[math]\displaystyle{ \rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] }[/math]

[math]\displaystyle{ \rho I\frac{\partial^{2}\varphi}{\partial t^{2}} = \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right) }[/math]

где искомыми величинами являются [math]\displaystyle{ w(x,t) }[/math] (отклонение балки) и [math]\displaystyle{ \varphi(x,t) }[/math] (угловое отклонение). Заметим, что в отличие от теории изгиба балок Эйлера-Бернулли угловое отклонение является отдельной переменной, а не приближается наклоном отклонения. Кроме того,

[math]\displaystyle{ \rho }[/math] — плотность материала балки (не линейная плотность).
[math]\displaystyle{ A }[/math] — площадь сечения балки.
[math]\displaystyle{ E }[/math] — модуль упругости.
[math]\displaystyle{ G }[/math] — модуль сдвига.
[math]\displaystyle{ I }[/math] — второй момент площади сечения.
[math]\displaystyle{ \kappa }[/math] — называется коэффициентом сдвига Тимошенко, который зависит от формы балки. Для прямоугольного сечения балки [math]\displaystyle{ \kappa = 5/6 }[/math].
[math]\displaystyle{ q(x,t) }[/math] — распределенная нагрузка (сила приложенная к единице длины).
[math]\displaystyle{ m := \rho A }[/math]
[math]\displaystyle{ J := \rho I }[/math]

Эти параметры не обязательно постоянные.

Дли линейной упругой изотропной однородной балки постоянного сечения эти два уравнения можно скомбинировть в следующее уравнение^[4]^[5]

[math]\displaystyle{ EI~\cfrac{\partial^4 w}{\partial x^4} + m~\cfrac{\partial^2 w}{\partial t^2} - \left(J + \cfrac{E I m}{k A G}\right)\cfrac{\partial^4 w}{\partial x^2~\partial t^2} + \cfrac{m J}{k A G}~\cfrac{\partial^4 w}{\partial t^4} = q(x,t) + \cfrac{J}{k A G}~\cfrac{\partial^2 q}{\partial t^2} - \cfrac{EI}{k A G}~\cfrac{\partial^2 q}{\partial x^2} }[/math]

Вывод комбинированного уравнения изгиба балки Тимошенко

Уравнения, которым подчиняется изгиб однородной балки постоянного сечения по Тимошенко, имеют вид

[math]\displaystyle{ \begin{align} (1) & & \quad m~\frac{\partial^2 w}{\partial t^2} & = \kappa AG~\left(\frac{\partial^2 w}{\partial x^2} - \frac{\partial \varphi}{\partial x}\right) + q(x,t) ~;~~ m := \rho A \\ (2) & & \quad J~\frac{\partial^2 \varphi}{\partial t^2} & = EI~\frac{\partial^2 \varphi}{\partial x^2} + \kappa AG~\left(\frac{\partial w}{\partial x} - \varphi\right) ~;~~ J := \rho I \end{align} }[/math]

Из уравнения (1) (предполагая достаточную гладкость) получаем

[math]\displaystyle{ \begin{align} (3) & & \quad \frac{\partial \varphi}{\partial x} & = -\cfrac{m}{\kappa AG}~\frac{\partial^2 w}{\partial t^2} + \frac{\partial^2 w}{\partial x^2} + \cfrac{q}{\kappa AG} \\ (4) & & \quad \frac{\partial^2 q}{\partial t^2} & = m~\cfrac{\partial^4 w}{\partial t^4} - \kappa AG~\left(\cfrac{\partial^4 w}{\partial x^2\partial t^2} - \cfrac{\partial^3\varphi}{\partial x\partial t^2}\right) \end{align} }[/math]

Из уравнения (3) (опять же при достаточной гладкости) можно написать

[math]\displaystyle{ (5) \qquad \cfrac{\partial^3\varphi}{\partial x^3} = -\cfrac{m}{\kappa AG}~\cfrac{\partial^4 w}{\partial x^2\partial t^2} + \cfrac{\partial^4 w}{\partial x^4} + \cfrac{1}{\kappa AG}~\frac{\partial^2 q}{\partial x^2} }[/math]

Дифференцируя уравнение (2) получаем

[math]\displaystyle{ (6) \qquad \cfrac{\partial^3\varphi}{\partial x \partial t^2} = \cfrac{EI}{J}~\cfrac{\partial^3 \varphi}{\partial x^3} + \cfrac{\kappa AG}{J}~\left(\frac{\partial^2 w}{\partial x^2} - \frac{\partial \varphi}{\partial x}\right) }[/math]

Из уравнений (4) и (6) пишем

[math]\displaystyle{ (7) \qquad \cfrac{1}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} -\cfrac{m}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} + \cfrac{\partial^4 w}{\partial x^2\partial t^2} = \cfrac{EI}{J}~\cfrac{\partial^3 \varphi}{\partial x^3} + \cfrac{\kappa AG}{J}~\left(\frac{\partial^2 w}{\partial x^2} - \frac{\partial \varphi}{\partial x}\right) }[/math]

Из уравнений (3) и (7) получаем

[math]\displaystyle{ (8) \qquad \cfrac{1}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} -\cfrac{m}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} + \cfrac{\partial^4 w}{\partial x^2\partial t^2} = \cfrac{EI}{J}~\cfrac{\partial^3 \varphi}{\partial x^3} + \cfrac{m}{J}~\frac{\partial^2 w}{\partial t^2} - \cfrac{q}{J} }[/math]

Подставляя уравнение (5) в уравнение (8) получаем

[math]\displaystyle{ (9) \qquad \cfrac{J}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} -\cfrac{mJ}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} + J~\cfrac{\partial^4 w}{\partial x^2\partial t^2} = -\cfrac{mEI}{\kappa AG}~\cfrac{\partial^4 w}{\partial x^2\partial t^2} + EI~\cfrac{\partial^4 w}{\partial x^4} + \cfrac{EI}{\kappa AG}~\frac{\partial^2 q}{\partial x^2} + m~\frac{\partial^2 w}{\partial t^2} - q }[/math]

Преобразуя это уравнение получаем

[math]\displaystyle{ EI~\cfrac{\partial^4 w}{\partial x^4} + m~\frac{\partial^2 w}{\partial t^2} - \left(J+\cfrac{mEI}{\kappa AG}\right)~\cfrac{\partial^4 w}{\partial x^2 \partial t^2} + \cfrac{mJ}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} = q + \cfrac{J}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} - \cfrac{EI}{\kappa A G}~\frac{\partial^2 q}{\partial x^2}\quad\square }[/math]

Уравнение Тимошенко предсказывает наличие критической частоты [math]\displaystyle{ \omega_C=2 \pi f_c=\sqrt{\frac{\kappa GA}{\rho I}}. }[/math] Для нормальных мод уравнение Тимошенко может быть решено. Поскольку это уравнение четвертого порядка, то у него существует четыре независимых решения, два осцилляторных и два быстро затухающих при частоте ниже [math]\displaystyle{ f_c }[/math]. Для частот выше [math]\displaystyle{ f_c }[/math] все решения осцилляторны и, как следствие этого, возникает второй спектр.^[6]

Осевые эффекты

Если отклонение балки задается в виде

[math]\displaystyle{ u_x(x,y,z,t) = u_0(x,t)-z~\varphi(x,t) ~;~~ u_y(x,y,z,t) = 0 ~;~~ u_z(x,y,z,t) = w(x,t) }[/math]

где [math]\displaystyle{ u_0 }[/math] есть дополнительное отклонение в направлении оси [math]\displaystyle{ x }[/math], тогда основное уравнение изгиба балки по Тимошенко обретает вид

[math]\displaystyle{ \begin{align} m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t) \\ J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right) \end{align} }[/math]

где [math]\displaystyle{ J = \rho I }[/math] и [math]\displaystyle{ N(x,t) }[/math] приложенная извне осевая сила. Любая внешняя осевая сила уравновешивается напряжением деформации

[math]\displaystyle{ N_{xx}(x,t) = \int_{-h}^{h} \sigma_{xx}~dz }[/math]

где [math]\displaystyle{ \sigma_{xx} }[/math] — осевое напряжение. Толщина балки здесь считается равной [math]\displaystyle{ 2h }[/math].

Комбинированное уравнение изгиба балки с учетом осевой силы имеет вид

[math]\displaystyle{ EI~\cfrac{\partial^4 w}{\partial x^4} + N~\cfrac{\partial^2 w}{\partial x^2} + m~\frac{\partial^2 w}{\partial t^2} - \left(J+\cfrac{mEI}{\kappa AG}\right)~\cfrac{\partial^4 w}{\partial x^2 \partial t^2} + \cfrac{mJ}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} = q + \cfrac{J}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} - \cfrac{EI}{\kappa A G}~\frac{\partial^2 q}{\partial x^2} }[/math]

Затухание (демпфирование)

Если, помимо учета осевых сил, мы предположим также наличие демпфирующей силы, которая пропорциональна скорости в виде

[math]\displaystyle{ \eta(x)~\cfrac{\partial w}{\partial t} }[/math]

то связанные основные уравнения изгиба балки Тимошенко становятся равными

[math]\displaystyle{ m \frac{\partial^{2}w}{\partial t^{2}} + \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t), }[/math]

[math]\displaystyle{ J \frac{\partial^{2}\varphi}{\partial t^{2}} = N\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right), }[/math] а комбинированное уравнение приобретает вид

[math]\displaystyle{ \begin{align} EI~\cfrac{\partial^4 w}{\partial x^4} & + N~\cfrac{\partial^2 w}{\partial x^2} + m~\frac{\partial^2 w}{\partial t^2} - \left(J+\cfrac{mEI}{\kappa AG}\right)~\cfrac{\partial^4 w}{\partial x^2 \partial t^2} + \cfrac{mJ}{\kappa AG}~\cfrac{\partial^4 w}{\partial t^4} + \cfrac{J \eta(x)}{\kappa AG}~\cfrac{\partial^3 w}{\partial t^3} \\ & -\cfrac{EI}{\kappa AG}~\cfrac{\partial^2}{\partial x^2}\left(\eta(x)\cfrac{\partial w}{\partial t}\right) + \eta(x)\cfrac{\partial w}{\partial t} = q + \cfrac{J}{\kappa AG}~\frac{\partial^2 q}{\partial t^2} - \cfrac{EI}{\kappa A G}~\frac{\partial^2 q}{\partial x^2} \end{align} }[/math]

Подобный анзац для демпфирующей силы (похожий на силу вязкости) несколько нереалистичен поскольку вязкость приводит к независящей от частоты амплитудно-зависимой скорости затухания колебаний балки, тогда как эмпирические измерения показывают, что затухание слабо зависит от частоты и сильно зависит от амплитуды отклонения балки.

Коэффициент сдвига

Определить коэффициента сдвига не так-то просто, к тому же неоднозначно (существует несколько способов его определения). В целом он должен удовлетворять условию:

[math]\displaystyle{ \int_A \tau dA = \kappa A G \varphi\, }[/math] .

Коэффициент сдвига зависит от коэффициента Пуассона. Попытки получить точное выражение для него предпринимались многими учёными, включая Степана Прокофьевича Тимошенко,^[7] Raymond D. Mindlin,^[8] G. R. Cowper,^[9] N. G. Stephen,^[10] J. R. Hutchinson^[11] и другими (см. также вывод уравнений изгиба балки Тимошенко с помощью теории изгиба балки основанной на вариационном-асимптотическом методе в книге Khanh C. Le^[12] который приводит к различным сдвиговым коэффициентам в статическом и динамическом случаях). В инженерной практике выражений Тимошенко^[13] вполне достаточно в большинстве случаев. В 1975 году Kaneko^[14] опубликовал весьма хороший обзор по коэффициенту сдвига. Позднее новые экспериментальные данные показали, что коэффициент сдвига недооценивается.^[15]^[16]

Согласно работе Cowper 1966 года для цельного прямоугольного сечения балки

[math]\displaystyle{ \kappa = \cfrac{10(1+\nu)}{12+11\nu} }[/math]

и для цельной балки круглого сечения

[math]\displaystyle{ \kappa = \cfrac{6(1+\nu)}{7+6\nu} }[/math].

См. также

Литература

↑ Timoshenko, S. P., 1921, On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 744.
↑ Timoshenko, S. P., 1922, On the transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 125.
↑ Timoshenko’s Beam Equations (неопр.). Дата обращения: 5 января 2019. Архивировано 15 октября 2007 года.
↑ Thomson, W. T., 1981, Theory of Vibration with Applications, second edition. Prentice-Hall, New Jersey.
↑ Rosinger, H. E. and Ritchie, I. G., 1977, On Timoshenko’s correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys., vol. 10, pp. 1461—1466.
↑ «Experimental study of the Timoshenko beam theory predictions», A. Díaz-de-Anda, J. Flores, L. Gutiérrez, R.A. Méndez-Sánchez, G. Monsivais, and A. Morales, Journal of Sound and Vibration, Volume 331, Issue 26, 17 December 2012, pp. 5732-5744.
↑ Timoshenko, Stephen P., 1932, Schwingungsprobleme der Technik, Julius Springer.
↑ Mindlin, R. D., Deresiewicz, H., 1953, Timoshenko’s Shear Coefficient for Flexural Vibrations of Beams, Technical Report No. 10, ONR Project NR064-388, Department of Civil Engineering, Columbia University, New York, N.Y.
↑ Cowper, G. R., 1966, «The Shear Coefficient in Timoshenko’s Beam Theory», J. Appl. Mech., Vol. 33, No.2, pp. 335—340.
↑ Stephen, N. G., 1980. «Timoshenko’s shear coefficient from a beam subjected to gravity loading», Journal of Applied Mechanics, Vol. 47, No. 1, pp. 121—127.
↑ Hutchinson, J. R., 1981, «Transverse vibration of beams, exact versus approximate solutions», Journal of Applied Mechanics, Vol. 48, No. 12, pp. 923—928.
↑ Le, Khanh C., 1999, Vibrations of shells and rods, Springer.
↑ Stephen Timoshenko, James M. Gere. Mechanics of Materials. Van Nostrand Reinhold Co., 1972. pages 207.
↑ Kaneko, T., 1975, «On Timoshenko’s correction for shear in vibrating beams», J. Phys. D: Appl. Phys., Vol. 8, pp. 1927—1936.
↑ «Experimental check on the accuracy of Timoshenko’s beam theory», R. A. Méndez-Sáchez, A. Morales, J. Flores, Journal of Sound and Vibration 279 (2005) 508—512.
↑ «On the Accuracy of the Timoshenko Beam Theory Above the Critical Frequency: Best Shear Coefficient», J. A. Franco-Villafañe and R. A. Méndez-Sánchez, Journal of Mechanics, January 2016, pp. 1-4. DOI: 10.1017/jmech.2015.104.

[Timo1-1] Timoshenko, S. P., 1921, On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 744.

[Timo2-2] Timoshenko, S. P., 1922, On the transverse vibrations of bars of uniform cross-section, Philosophical Magazine, p. 125.

[3] Timoshenko’s Beam Equations (неопр.). Дата обращения: 5 января 2019. Архивировано 15 октября 2007 года.

[Thomson-4] Thomson, W. T., 1981, Theory of Vibration with Applications, second edition. Prentice-Hall, New Jersey.

[Rosinger-5] Rosinger, H. E. and Ritchie, I. G., 1977, On Timoshenko’s correction for shear in vibrating isotropic beams, J. Phys. D: Appl. Phys., vol. 10, pp. 1461—1466.

[6] «Experimental study of the Timoshenko beam theory predictions», A. Díaz-de-Anda, J. Flores, L. Gutiérrez, R.A. Méndez-Sánchez, G. Monsivais, and A. Morales, Journal of Sound and Vibration, Volume 331, Issue 26, 17 December 2012, pp. 5732-5744.

[7] Timoshenko, Stephen P., 1932, Schwingungsprobleme der Technik, Julius Springer.

[8] Mindlin, R. D., Deresiewicz, H., 1953, Timoshenko’s Shear Coefficient for Flexural Vibrations of Beams, Technical Report No. 10, ONR Project NR064-388, Department of Civil Engineering, Columbia University, New York, N.Y.

[9] Cowper, G. R., 1966, «The Shear Coefficient in Timoshenko’s Beam Theory», J. Appl. Mech., Vol. 33, No.2, pp. 335—340.

[10] Stephen, N. G., 1980. «Timoshenko’s shear coefficient from a beam subjected to gravity loading», Journal of Applied Mechanics, Vol. 47, No. 1, pp. 121—127.

[11] Hutchinson, J. R., 1981, «Transverse vibration of beams, exact versus approximate solutions», Journal of Applied Mechanics, Vol. 48, No. 12, pp. 923—928.

[12] Le, Khanh C., 1999, Vibrations of shells and rods, Springer.

[13] Stephen Timoshenko, James M. Gere. Mechanics of Materials. Van Nostrand Reinhold Co., 1972. pages 207.

[14] Kaneko, T., 1975, «On Timoshenko’s correction for shear in vibrating beams», J. Phys. D: Appl. Phys., Vol. 8, pp. 1927—1936.

[15] «Experimental check on the accuracy of Timoshenko’s beam theory», R. A. Méndez-Sáchez, A. Morales, J. Flores, Journal of Sound and Vibration 279 (2005) 508—512.

[16] «On the Accuracy of the Timoshenko Beam Theory Above the Critical Frequency: Best Shear Coefficient», J. A. Franco-Villafañe and R. A. Méndez-Sánchez, Journal of Mechanics, January 2016, pp. 1-4. DOI: 10.1017/jmech.2015.104.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]