Изгиб (механика)

Изгиб — в сопротивлении материалов вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев, изменение кривизны/искривление срединной поверхности пластины или оболочки. Изгиб связан с возникновением в поперечных сечениях бруса или оболочки изгибающих моментов. Прямой изгиб балки возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.

Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.

Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом.

Классическая теория изгиба балок (теория Эйлера — Бернулли)

Данная теория является базовой для аналитических расчётов балок и рам.

Основные гипотезы

• Гипотеза плоских сечений (гипотеза Бернулли): сечения балки, плоские и нормальные к оси до деформации, остаются после деформации плоскими и нормальными к изогнутой оси балки. Таким образом, деформация сдвига слоёв относительно друг друга не учитывается. Единственным напряжением, рассматриваемым в этой теории, является осевое напряжение [math]\displaystyle{ \sigma_z }[/math];

• Перемещения и деформации предполагаются малыми. Балка предполагается нерастяжимой;

• Размеры сечения балки предполагаются малыми по сравнению с радиусом кривизны оси балки;

• Материал рассматривается как линейно упругий согласно закону Гука.

Вывод уравнений, связывающих силовые факторы с напряжениями и деформациями

Геометрические соотношения

Из основных гипотез следует, что деформация [math]\displaystyle{ \varepsilon_z }[/math] распределена по высоте сечения по линейному закону. В соответствии с законом Гука,

[math]\displaystyle{ \sigma_z=E\varepsilon_z }[/math]

то есть напряжения также распределены по линейному закону.

В сечении балки (в плоском случае) возникают изгибающий момент [math]\displaystyle{ M_x }[/math], поперечная сила [math]\displaystyle{ Q_y }[/math] и продольная сила [math]\displaystyle{ N }[/math]. На сечение действует внешняя распределённая нагрузка [math]\displaystyle{ q }[/math].

Элемент балки, вырезанный двумя смежными поперечными сечениями, в деформированном состоянии

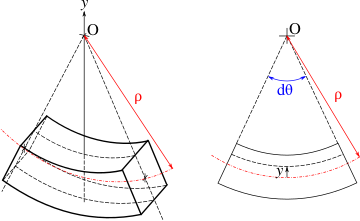
Рассмотрим два смежных сечения, расположенных на расстоянии [math]\displaystyle{ dz }[/math] друг от друга. В деформированном состоянии они развёрнуты на угол [math]\displaystyle{ d\theta }[/math] друг относительно друга. Так как верхние слои растянуты, а нижние сжаты, то очевидно, что существует нейтральный слой, остающийся нерастянутым. На рисунке он выделен красным. Изменение радиуса кривизны нейтрального слоя записывается следующим образом:

[math]\displaystyle{ \frac{1}{\rho}=\frac{d\theta}{dz} }[/math]

Приращение длины отрезка АВ, находящегося на расстоянии [math]\displaystyle{ y }[/math] от нейтральной оси, выражается следующим образом:

[math]\displaystyle{ \Delta l=(y+\rho)d\theta-\rho d\theta=y d\theta }[/math]

Таким образом, деформация:

[math]\displaystyle{ \varepsilon_z=\frac{\Delta l}{l}=\frac{y d\theta}{\rho d\theta}=\frac{y}{\rho} }[/math]

Силовые соотношения

Напряжение (по закону Гука):

[math]\displaystyle{ \sigma_z=E\varepsilon_z=E\frac{y}{\rho} }[/math]

Свяжем напряжение с силовыми факторами, возникающими в сечении. Осевая сила выражается следующим образом:

[math]\displaystyle{ N=\int \limits_A^{\color{White}.} {\sigma_z} \,dA=\int \limits_A^{\color{White}.} {E\frac{y}{\rho}} \,dA=\frac{E}{\rho} \int \limits_A^{\color{White}.} y \,dA }[/math]

Интеграл в последнем выражении представляет собой статический момент сечения относительно оси [math]\displaystyle{ x }[/math]. Принято брать в качестве оси [math]\displaystyle{ x }[/math] центральную ось сечения, такую, что

[math]\displaystyle{ S_x=\int \limits_A^{\color{White}.} y \,dA =0 }[/math]

Таким образом, [math]\displaystyle{ N=0 }[/math]. Изгибающий момент выражается следующим образом:

[math]\displaystyle{ M_x=\int \limits_A^{\color{White}.} {\sigma_z y} \,dA=\frac{E}{\rho} \int \limits_A^{\color{White}.} {y^2} \,dA=\frac{E}{\rho} J_x }[/math]

где [math]\displaystyle{ J_x=\int \limits_A^{\color{White}.} {y^2} \,dA }[/math] — момент инерции сечения относительно оси [math]\displaystyle{ x }[/math].

Напряжения в сечении могут также приводиться к моменту [math]\displaystyle{ M_y }[/math]. Чтобы этого не произошло, необходимо выполнение условия:

[math]\displaystyle{ M_y=\frac{E}{\rho} \int \limits_A^{\color{White}.} {yx} \,dA=\frac{E}{\rho} J_{xy}=0 }[/math]

то есть центробежный момент инерции должен быть равен нулю, и ось [math]\displaystyle{ y }[/math] должна быть одной из главных осей сечения.

Таким образом, кривизна изогнутой оси балки связана с изгибающим моментом выражением:

[math]\displaystyle{ \frac{1}{\rho}=\frac{M_x}{EJ_x} }[/math]

Распределение напряжений по высоте сечения выражается формулой:

[math]\displaystyle{ \sigma=\frac{M_x}{J_x} y }[/math]

Максимальное напряжение в сечении выражается формулой:

[math]\displaystyle{ \sigma_{max}=\frac{M_x}{J_x} \frac{h}{2}=\frac{M_x}{W_x} }[/math]

где [math]\displaystyle{ W_x=\frac{J_x}{\frac{h}{2}} }[/math] — момент сопротивления сечения изгибу, [math]\displaystyle{ h }[/math] — высота сечения балки.

Величины [math]\displaystyle{ J_x }[/math] и [math]\displaystyle{ W_x }[/math] для простых сечений (круглое, прямоугольное) вычисляются аналитически. Для круглого сечения диаметром [math]\displaystyle{ d }[/math]:

[math]\displaystyle{ J_x=\frac{\pi d^4}{64} }[/math]

[math]\displaystyle{ W_x=\frac{\pi d^3}{32} }[/math]

Для прямоугольного сечения высотой [math]\displaystyle{ h }[/math] и шириной [math]\displaystyle{ b }[/math]

[math]\displaystyle{ J_x=\frac{bh^3}{12} }[/math]

[math]\displaystyle{ W_x=\frac{bh^2}{6} }[/math]

Для более сложных сечений (например, швеллер, двутавр), имеющих стандартизованные размеры, эти величины приведены в справочной литературе.

Изгибающий момент в сечении может быть получен методом сечений (если балка статически определима) или методами сил/перемещений.

Дифференциальные уравнения равновесия. Определение перемещений

Основными перемещениями, возникающими при изгибе, являются прогибы [math]\displaystyle{ v }[/math] в направлении оси [math]\displaystyle{ y }[/math]. Необходимо связать их с изгибающим моментом в сечении. Запишем точное соотношение, связывающее прогибы и кривизну изогнутой оси:

[math]\displaystyle{ \frac{1}{\rho}=\frac{v''}{(1+v'^2)^{\frac{3}{2}}} }[/math]

Так как прогибы и углы поворота предполагаются малыми, то величина

[math]\displaystyle{ v'^2=\left (\mathrm{tg}\,(\theta) \right )^2\approx\theta^2 }[/math]

является малой. Следовательно,

[math]\displaystyle{ \frac{1}{\rho} \approx v'' }[/math]

Значит,

[math]\displaystyle{ v''=\frac{M_x}{EJ_x} }[/math]

Запишем уравнение равновесия сечения в направлении оси [math]\displaystyle{ y }[/math]:

[math]\displaystyle{ Q_y+qdz-Q_y-dQ_y=0\Rrightarrow\frac{dQ}{dz}=q }[/math]

Запишем уравнение равновесия моментов относительно оси [math]\displaystyle{ x }[/math]:

[math]\displaystyle{ M_x+Q\,dz+q\,dz\frac{\,dz}{2}-M_x-\,dM_x=0 }[/math]

Величина [math]\displaystyle{ q\,dz\frac{\,dz}{2} }[/math] имеет 2-й порядок малости и может быть отброшена. Следовательно,

[math]\displaystyle{ \frac{\,dM_x}{\,dz}=Q_y }[/math]

Таким образом, имеется 3 дифференциальных уравнения. К ним добавляется уравнение для перемещений:

[math]\displaystyle{ \frac{\,dv}{\,dz}=\mathrm{tg}\,\theta\approx\theta }[/math]

В векторно-матричной форме система записывается следующим образом:

[math]\displaystyle{ \frac{\,d\overrightarrow{Z}}{\,dz}+A\overrightarrow{Z}=\overrightarrow{b} }[/math]

где

[math]\displaystyle{ A=\begin{Bmatrix} 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & -\displaystyle\frac{1}{EJ_x(z)} & 0 & 0 \\ 0 & 0 & -1 & 0 \end{Bmatrix} }[/math]

Вектор состояния системы:

[math]\displaystyle{ \overrightarrow{Z}=(Q,M,\theta,v)^T }[/math]

Вектор внешней нагрузки:

[math]\displaystyle{ \overrightarrow{b}=(q,0,0,0)^T }[/math]

Это дифференциальное уравнение может быть использовано для расчёта многоопорных балок с переменным по длине моментом инерции сечения и сложным образом распределёнными нагрузками. Для расчёта простых балок применяются упрощённые методы. В сопротивлении материалов при расчете статически определимых балок изгибающий момент находится методом сечений. Уравнение

[math]\displaystyle{ v''=\frac{M_x}{EJ_x} }[/math]

интегрируется дважды:

[math]\displaystyle{ v'=\theta(z)=\int \frac{M_x(z)}{EJ_x} \,dz +C_1 }[/math]

[math]\displaystyle{ v(z)= \int \left (\int \frac{M_x(z)}{EJ_x} \,dz \right ) \,dz +C_1z+C_2 }[/math]

Константы [math]\displaystyle{ C_1 }[/math], [math]\displaystyle{ C_2 }[/math] находятся из граничных условий, наложенных на балку. Так, для консольной балки, изображённой на рисунке:

Консольная балка, нагруженная силой на конце

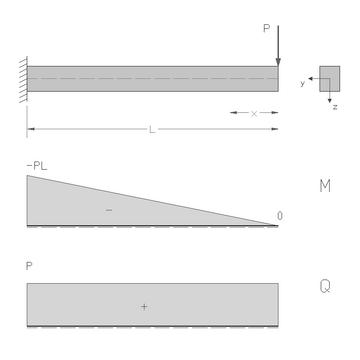
[math]\displaystyle{ M_x(z)=-P(L-z) }[/math]

[math]\displaystyle{ \theta(z)=-PL\frac{z}{EJ_x}+P\frac{z^2}{2EJ_x} +C_1 }[/math]

[math]\displaystyle{ v(z)=-PL\frac{z^2}{2EJ_x}+P\frac{z^3}{6EJ_x}+C_1z+C_2 }[/math]

Граничные условия:

[math]\displaystyle{ \theta(0)=0\Rrightarrow C_1=0 }[/math]

[math]\displaystyle{ v(0)=0\Rrightarrow C_2=0 }[/math]

Таким образом,

[math]\displaystyle{ \theta(z)=-PL\frac{z}{EJ_x}+P\frac{z^2}{2EJ_x} }[/math]

[math]\displaystyle{ v(z)=-PL\frac{z^2}{2EJ_x}+P\frac{z^3}{6EJ_x} }[/math]

Теория изгиба балок Тимошенко

Данная теория базируется на тех же гипотезах, что и классическая, однако гипотеза Бернулли модифицируется: предполагается, что сечения, бывшие до деформации плоскими и нормальными к оси балки, остаются плоскими, но перестают быть нормальными к изогнутой оси. Таким образом, данная теория учитывает деформацию сдвига и касательные напряжения. Учёт касательных напряжений очень важен для расчёта композитов и деталей из дерева, так как их разрушение может происходить за счёт разрушения связующего при сдвиге.

Основные зависимости:

[math]\displaystyle{ M=EJ\frac{\,d\theta}{\,dz} }[/math]

[math]\displaystyle{ Q=\frac{GF}{\alpha}\left (\theta-\frac{\,dv}{\,dz}\right) }[/math]

где [math]\displaystyle{ G }[/math] — модуль сдвига материала балки, [math]\displaystyle{ F }[/math] — площадь сечения, [math]\displaystyle{ \alpha }[/math] — коэффициент, учитывающий неравномерность распределения касательных напряжений по сечению и зависящий от его формы. Величина

[math]\displaystyle{ \gamma=\theta-\frac{\,dv}{\,dz} }[/math]

представляет собой угол сдвига.

Изгиб балок на упругом основании

Данной расчётной схемой моделируются железнодорожные рельсы, а также корабли (в первом приближении).

Упругое основание рассматривается как множество не связанных друг с другом пружинок.

Простейший метод расчёта основан на гипотезе Винклера: реакция упругого основания пропорциональна прогибу в точке и направлена навстречу ему:

[math]\displaystyle{ p=-k\cdot v }[/math]

где [math]\displaystyle{ v }[/math] — прогиб;

[math]\displaystyle{ p }[/math] — реакция (на единицу длины балки);

[math]\displaystyle{ k }[/math] — коэффициент пропорциональности (называемый коэффициентом постели).

При этом основание считается двусторонним, то есть реакция возникает как при вдавливании балки в основание, так и при её отрыве от основания. Гипотеза Бернулли сохраняется.

Дифференциальное уравнение изгиба балки на упругом основании имеет вид:

[math]\displaystyle{ \frac{d^2}{dz^2}\left(EJ_x(z)\frac{d^2v}{dz^2}\right)+k(z)\cdot v=q(z) }[/math]

где [math]\displaystyle{ v(z) }[/math] — прогиб;

[math]\displaystyle{ EJ_x(z) }[/math] — изгибная жёсткость (могущая быть переменной по длине);

[math]\displaystyle{ k(z) }[/math] — переменный по длине коэффициент постели;

[math]\displaystyle{ q(z) }[/math] — распределённая нагрузка на балку.

При постоянной жёсткости и коэффициенте постели уравнение может быть записано в виде:

[math]\displaystyle{ EJ_x\frac{d^4v}{dz^4}+k\cdot v=q(z) }[/math]

или

[math]\displaystyle{ \frac{d^4v}{dz^4}+4m^4\cdot v=q(z) }[/math]

где обозначено

[math]\displaystyle{ 4m^4=\frac{k}{EJ_x} }[/math]

Изгиб бруса большой кривизны

Для балок, радиус кривизны оси которых [math]\displaystyle{ \rho_0 }[/math] соизмерим с высотой сечения [math]\displaystyle{ h }[/math], то есть:

[math]\displaystyle{ \frac{h}{\rho_0}\gt 0,2 }[/math]

распределение напряжений по высоте отклоняется от линейного, а нейтральная линия не совпадает с осью сечения (которая проходит через центр тяжести сечения). Такая расчетная схема используется, например, для расчёта звеньев цепей и крюков подъёмных кранов.

Поперечное сечение

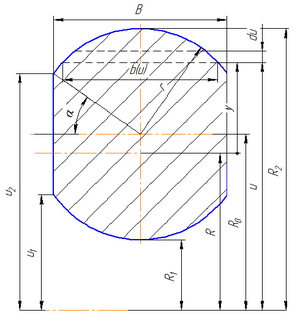
Формула для распределения напряжений имеет вид:

[math]\displaystyle{ \sigma=\frac{M}{F\cdot e}\cdot\frac{y}{R+y} }[/math]

где [math]\displaystyle{ M }[/math] — изгибающий момент в сечении;

[math]\displaystyle{ R }[/math] — радиус нейтральной линии сечения;

[math]\displaystyle{ F }[/math] — площадь сечения;

[math]\displaystyle{ e=R_0-R }[/math] — эксцентриситет;

[math]\displaystyle{ y }[/math] — координата по высоте сечения, отсчитываемая от нейтральной линии.

Радиус нейтральной линии определяется по формуле:

[math]\displaystyle{ R=\int\frac{\,dF}{u}=\int\limits_{R_1}^{R_2}\frac{b(u)\,du}{u} }[/math]

Интеграл берётся по площади сечения, координата [math]\displaystyle{ u }[/math] отсчитывается от центра кривизны. Справедливы также приближённые формулы:

[math]\displaystyle{ e=\frac{J_x}{R_0\cdot F} }[/math]

[math]\displaystyle{ r_0=R_0-\frac{J_x}{R_0\cdot F} }[/math]

Для часто используемых сечений имеются аналитические формулы. Для прямоугольного сечения высотой [math]\displaystyle{ h }[/math]:

[math]\displaystyle{ R=\frac{h}{\ln\displaystyle\frac{R_0+\frac{h}{2}}{R_0-\frac{h}{2}}}=\frac{h}{\ln\displaystyle\frac{R_2}{R_1}} }[/math]

где [math]\displaystyle{ R_1, R_2 }[/math] — радиусы кривизны внутренней и наружной поверхности балки соответственно.

Для круглого сечения:

[math]\displaystyle{ R=\frac{R_0+\sqrt{R^2_0-r^2}}{2} }[/math]

где [math]\displaystyle{ r }[/math] — радиус сечения.

Проверка прочности балки

В большинстве случаев прочность балки определяется по максимальным допускаемым напряжениям:

[math]\displaystyle{ \sigma_{max}\lt \frac{\sigma_T}{n_T} }[/math]

где [math]\displaystyle{ \sigma_T }[/math] — предел текучести материала балки, [math]\displaystyle{ n_T }[/math] — коэффициент запаса по текучести. В случае хрупких материалов:

[math]\displaystyle{ \sigma_{max}\lt \frac{\sigma_b}{n_b} }[/math]

где [math]\displaystyle{ \sigma_b }[/math] — предел прочности материала балки, [math]\displaystyle{ n_b }[/math] — коэффициент запаса по прочности.

В случае пластичных материалов эти формулы могут существенно занижать значение нагрузки, при котором балка теряет свою несущую способность. Фактически несущая способность теряется лишь в случае, если в каком-либо сечении весь материал переходит в пластическое состояние. Тогда в сечении могут возникать недопустимые перемещения (образуется так называемый пластический шарнир). Если принимать в качестве диаграммы растяжения-сжатия диаграмму Прандтля, то предельный изгибающий момент [math]\displaystyle{ M_{pr} }[/math] для стержня прямоугольного сечения шириной [math]\displaystyle{ b }[/math] и высотой [math]\displaystyle{ h }[/math] выражается формулой:

[math]\displaystyle{ M_{pr}=\frac{1}{4} bh^2\sigma_T }[/math]

Динамическое нагружение балок

Собственные колебания

Рассмотрим балку с плотностью материала [math]\displaystyle{ \rho }[/math], площадью поперечного сечения [math]\displaystyle{ A }[/math], изгибной жёсткостью [math]\displaystyle{ EJ }[/math]. Уравнение собственных колебаний имеет вид:

[math]\displaystyle{ \frac{\partial^2}{\partial z^2}\left(EJ\frac{\partial^2x}{\partial z^2}\right)+m_0 \frac{\partial^2x}{\partial t^2}=0 }[/math]

где [math]\displaystyle{ x(z,t) }[/math] — поперечное перемещение, [math]\displaystyle{ m_0=\rho A }[/math] — масса единицы длины стержня. Решение ищется в виде:

[math]\displaystyle{ x(z,t)=u(z)\cos(pt+\phi) }[/math]

Подставляя, получаем обыкновенное дифференциальное уравнение:

[math]\displaystyle{ \frac{d^2}{d z^2}\left(EJ\frac{d^2u}{d z^2}\right)-m_0 p^2u=0 }[/math]

Для балки постоянного сечения оно преобразуется к виду:

[math]\displaystyle{ \frac{d^4u}{dz^4}-\alpha^4u=0 }[/math]

где

[math]\displaystyle{ \alpha^4=\frac{p^2m_0}{EJ} }[/math]

Удобно представить решение с использованием функций Крылова:

[math]\displaystyle{ u=\sum_{i=1}^4C_iK_i(\alpha z) }[/math]

где функции Крылова:

[math]\displaystyle{ K_1(\alpha z)=\frac{1}{2}(\operatorname{ch}\alpha z+\cos\alpha z) }[/math]

[math]\displaystyle{ K_2(\alpha z)=\frac{1}{2}(\operatorname{sh}\alpha z+\sin\alpha z) }[/math]

[math]\displaystyle{ K_3(\alpha z)=\frac{1}{2}(\operatorname{ch}\alpha z-\cos\alpha z) }[/math]

[math]\displaystyle{ K_4(\alpha z)=\frac{1}{2}(\operatorname{sh}\alpha z-\sin\alpha z) }[/math]

а [math]\displaystyle{ C_i }[/math] — постоянные.

Функции Крылова связаны зависимостями:

[math]\displaystyle{ \frac{d}{dz}K_1(\alpha z)=\alpha K_4(\alpha z) }[/math]

[math]\displaystyle{ \frac{d}{dz}K_2(\alpha z)=\alpha K_1(\alpha z) }[/math]

[math]\displaystyle{ \frac{d}{dz}K_3(\alpha z)=\alpha K_2(\alpha z) }[/math]

[math]\displaystyle{ \frac{d}{dz}K_4(\alpha z)=\alpha K_3(\alpha z) }[/math]

Эти зависимости существенно упрощают запись граничных условий для балок:

[math]\displaystyle{ C_1=u_{z=0}; C_2=\frac{1}{\alpha}\left(\frac{du}{dz}\right)_{z=0}; C_3=\frac{1}{EJ\alpha^2}M_{z=0}; C_4=\frac{1}{EJ\alpha^3}Q_{z=0} }[/math]

На каждом конце балки задаются два граничных условия.

Уравнение собственных колебаний имеет бесконечно много решений. При этом, практический интерес, как правило, представляют только первые несколько из них, соответствующие низшим собственным частотам.

Общая формула для собственной частоты имеет вид:

[math]\displaystyle{ p_k=\lambda^2_k\sqrt{\frac{EJ}{m_0l^4}} }[/math]

Для однопролётных балок:

Закрепление		[math]\displaystyle{ \lambda_k }[/math]
Левый конец	Правый конец
Заделка	Заделка	[math]\displaystyle{ \lambda_1=4,73; }[/math][math]\displaystyle{ \lambda_2=7,853; }[/math]
Свободный	Свободный	[math]\displaystyle{ \lambda_1=0; }[/math][math]\displaystyle{ \lambda_2=0; }[/math] при k>2 [math]\displaystyle{ \lambda_k=\frac{2k+1}{2}\pi; }[/math]
Заделка	Шарнирное	[math]\displaystyle{ \lambda_1=3,927; }[/math][math]\displaystyle{ \lambda_2=7,069; }[/math] при k>2 [math]\displaystyle{ \lambda_k=\frac{4k+1}{4}\pi; }[/math]
Шарнирное	Шарнирное	[math]\displaystyle{ \lambda_k=k\pi }[/math]
Заделка	Свободный	[math]\displaystyle{ \lambda_1=1,875; }[/math][math]\displaystyle{ \lambda_2=4,694; }[/math] при k>2 [math]\displaystyle{ \lambda_k=\frac{2k-1}{2}\pi; }[/math]

См. также

• Удлинение на изгиб

Литература

• Бидерман В. Л. Теория механических колебаний: Учебник для вузов. — М.: Высш. школа, 1980. — 408 с.
• Феодосьев В. И. Сопротивление материалов. — М.: изд-во МГТУ им. Н. Э. Баумана, 1999

Ссылки

• Расчётные данные для типовых балок постоянного сечения