Строение звёзд

Диаграмма, показывающая строение Солнца. На врезке представлено строение солнечного пятна (англ. sunspot); на поверхности виден протуберанец (англ. prominence).

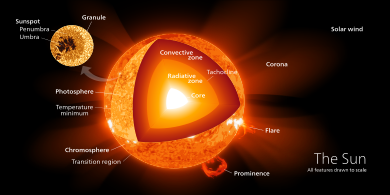
Звёзды различных масс и возрастов обладают различной внутренней структурой. Модели строения звезды подробно описывают внутреннюю структуру звезды и предоставляют подробные сведения о светимости, цвете и дальнейшей эволюции звезды.

Перенос энергии

Различные механизмы переноса энергии в звёздах. Если масса превышает солнечную более чем в 1,5 раза, центральную часть звезды занимает конвективная зона, во внешней части действует лучистый перенос энергии. Для звёзд промежуточных масс в центральной части действует лучистый перенос, во внешней области — конвективный. У маломассивных звёзд большая часть объёма представляет собой конвективную зону.

Различные слои внутри звезды переносят тепловую энергию различными способами: основными механизмами являются конвекция и лучистый перенос, но для белых карликов существенной также оказывается теплопроводность.

Конвекция является основным механизмом передачи энергии в том случае, когда градиент температуры достаточно велик для того, чтобы выделенный участок газа в звезде продолжал подниматься к поверхности, если подъём происходит медленно в ходе адиабатического процесса. В таком случае поднимающийся участок газа обладает плавучестью и продолжает подниматься, если оказывается теплее окружающего газа. Если же поднимающийся газ оказывается холоднее окружающегося вещества, то он впоследствии погрузится обратно на начальную высоту относительно центра звезды. В областях с маленьким градиентом температуры и достаточно малой непрозрачностью основным механизмом передачи энергии является лучистый перенос.

Внутреннее строение звезды на главной последовательности определяется во многом массой звезды.

У звёзд с массой от 0,3 до 1,5 масс Солнца, включая само Солнце, образование гелия происходит в основном в протон-протонных реакциях, при которых не возникает резкого градиента температуры. Следовательно, в центральной области звёзд таких масс перенос энергии осуществляется излучением. Внешние слои звёзд солнечной массы достаточно холодные для того, чтобы водород находился в нейтральном состоянии, и, следовательно, был непрозрачным для ультрафиолетового излучения, при этом механизмом переноса энергии является конвекция. Таким образом, звёзды солнечной массы обладают зоной лучистого переноса вблизи ядра и конвективной оболочкой во внешней части.

В массивных звёздах (массы более 1,5 масс Солнца) температура ядра превышает 1,8×10⁷ K, поэтому реакции преобразования водорода в гелий происходят в рамках CNO-цикла. В CNO-цикле темп энерговыделения пропорционален 15-й степени температуры, а в протон-протонном цикле — 4-й. Вследствие высокой чувствительности реакций CNO-цикла к температуре градиент температуры во внутренней части звезды достаточно велик для того, чтобы ядро стало конвективным. Во внешней части звезды градиент температуры меньше, но температура достаточно высока для того, чтобы водород был почти полностью ионизованным, оставаясь прозрачным для ультрафиолетового излучения. Следовательно, внешние области массивных звёзд являются областями лучистого переноса энергии.

Звёзды главной последовательности наименьших масс не обладают областью лучистого переноса, энергия передаётся внешним областям звезды посредством конвекции.

Уравнения, касающиеся строения звезды

Наиболее простая из обычно используемых моделей звёздной структуры представляет собой сферически-симметричную квазистатичную модель, в которой звезда находится в состоянии равновесия. Модель включает 4 основных дифференциальных уравнения первого порядка: два уравнения показывают, как меняется состояние вещества и давления в зависимости от радиуса, два других уравнения показывают, как от радиуса зависит температура и светимость.

При составлении уравнений строения звезды в предположении сферической симметрии рассматривается плотность вещества [math]\displaystyle{ \rho(r) }[/math], температура [math]\displaystyle{ T(r) }[/math], полное давление (вещества и излучения) [math]\displaystyle{ P(r) }[/math], светимость [math]\displaystyle{ l(r) }[/math] и темп энерговыделения в расчёте на единицу массы [math]\displaystyle{ \epsilon(r) }[/math] в сферической оболочке толщиной [math]\displaystyle{ \mbox{d}r }[/math] на расстоянии [math]\displaystyle{ r }[/math] от центра звезды. Предполагается, что звезда находится в локальном термодинамическом равновесии (ЛТР), поэтому температура является одинаковой для вещества и фотонов. Хотя ЛТР не всегда строго выполняется, поскольку температура в области под рассматриваемой оболочкой выше, а над ней — ниже, но данное приближение является применимым, поскольку длина свободного пробега [math]\displaystyle{ \lambda }[/math] гораздо меньше характерного масштаба изменения температуры (например, [math]\displaystyle{ \lambda \ll T/|\nabla T| }[/math]).

Первое уравнение представляет собой условие гидростатического равновесия: направленная от центра звезды сила, вызванная градиентом давления, уравновешивается силой гравитации.

[math]\displaystyle{ {\mbox{d} P \over \mbox{d} r} = - { G m \rho \over r^2 } }[/math],

где [math]\displaystyle{ m(r) }[/math] — полная масса внутри оболочки радиуса [math]\displaystyle{ r }[/math], G — гравитационная постоянная. Согласно уравнению непрерывности, полная масса возрастает при увеличении радиуса:

[math]\displaystyle{ {\mbox {d} m \over \mbox{d} r} = 4 \pi r^2 \rho . }[/math]

При интегрировании уравнения непрерывности массы от центра звезды ([math]\displaystyle{ r=0 }[/math]) до радиуса звезды ([math]\displaystyle{ r=R }[/math]) получается полная масса звезды.

Рассмотрение прохождения энергии сквозь сферическую оболочку приводит к уравнению для энергии:

[math]\displaystyle{ {\mbox{d} l \over \mbox{d} r} = 4 \pi r^2 \rho ( \epsilon - \epsilon_\nu ) }[/math],

где [math]\displaystyle{ \epsilon_\nu }[/math] — светимость, создаваемая в виде нейтрино (обычно покидают звезду, не взаимодействуя с обычным веществом), на единицу массы. За пределами ядра звезды, в котором происходят ядерные реакции, энергия не производится, поэтому светимость остаётся постоянной.

Уравнение переноса энергии может быть представлено в различных формах в зависимости от механизма переноса энергии. Для передачи энергии посредством теплопроводности (как, например, в белом карлике) уравнение для энергии имеет вид

[math]\displaystyle{ {\mbox{d} T \over \mbox{d} r} = - {1 \over k} { l \over 4 \pi r^2 }, }[/math]

где k — теплопроводность.

В случае лучистого переноса энергии, имеющего место во внутренних областях звёзд главной последовательности солнечной массы и внешних областях более массивных звёзд, уравнение имеет вид

[math]\displaystyle{ {\mbox{d} T \over \mbox{d} r} = - {3 \kappa \rho l \over 64 \pi r^2 \sigma T^3}, }[/math]

где [math]\displaystyle{ \kappa }[/math] — непрозрачность вещества, [math]\displaystyle{ \sigma }[/math] — Постоянная Стефана — Больцмана, постоянная Больцмана равна 1.

Для конвективного механизма переноса энергии строгой математической формулировки не существует, при этом необходимо учитывать турбулентность газа. Конвекцию обычно рассматривают в рамках теории пути смешения Прандтля. Газ представляется содержащим дискретные элементы, обладающие температурой, плотностью и давлением как у окружающего вещества, но движущиеся в звезде на характерные расстояния, называемые длиной смешения. Для одноатомного идеального газа в случае адиабатичности конвекции, означающей отсутствие обмена теплом между пузырями газа и окружающей средой, теория смешения даёт соотношение

[math]\displaystyle{ {\mbox{d} T \over \mbox{d} r} = \left(1 - {1 \over \gamma} \right) {T \over P } { \mbox{d} P \over \mbox{d} r}, }[/math]

где [math]\displaystyle{ \gamma = c_p / c_v }[/math] — показатель адиабаты (для полностью ионизованного идеального газа [math]\displaystyle{ \gamma = 5/3 }[/math]). Если конвекция не адиабатическая, в реальности градиент температуры не задаётся таким уравнением. Например, в Солнце конвекция вблизи ядра является адиабатической, но не у поверхности. Теория пути смешения содержит два свободных параметра, которые следует задавать в соответствии с наилучшей согласованностью с наблюдениями.

Также требуется уравнение состояния, связывающее давление, непрозрачность вещества и темп энерговыделения с плотностью, температурой, химическим составом и т. д. Уравнения состояния для давления могут включать соотношения идеального газа, давление излучения, давление вырожденных электронов. Параметр непрозрачности газа не получается выразить единой формулой. Существуют таблицы значений непрозрачности для различных химического состава, температуры и плотности. Компьютерные модели строения звёзд осуществляют интерполяцию на решётке плотность-температура для вычисления параметров непрозрачности или используют приближение некоторой функцией по значениям из таблиц. Похожая ситуация складывается для высокоточных вычислений уравнения состояния для давления. Темп энерговыделения в ядерных реакциях вычисляется на основе данных, полученных в ходе экспериментов в рамках ядерной физики. Вычисление параметров проводится для каждого шага реакции.

Решение данных уравнений совместно с граничными условиями полностью описывает поведение звезды. Обычно граничные условия устанавливают значения наблюдаемых параметров на поверхности ([math]\displaystyle{ r=R }[/math]) и в центре ([math]\displaystyle{ r=0 }[/math]) звезды: [math]\displaystyle{ P(R) = 0 }[/math] означает нулевое давление на поверхности звезды; [math]\displaystyle{ m(0) = 0 }[/math] означает отсутствие массы в самом центре звезды, что предполагает финитность плотности; [math]\displaystyle{ m(R) = M }[/math] — полная масса звезды; [math]\displaystyle{ T(R) = T_{eff} }[/math] — температура на поверхности является эффективной температурой звезды.

Хотя современные модели звёздной эволюции описывают основные особенности диаграммы цвет — величина, требуется внести значительные улучшения для устранения неопределённостей, связанных с неполными знаниями о переносе энергии. Учёт турбулентности остаётся одной из наиболее сложных задач. Некоторые группы исследователей разрабатывают упрощённые модели турбулентности в рамках трёхмерных вычислений.

Быстрое развитие

Указанная выше упрощённая модель нуждается в модификациях для ситуаций, когда изменение химического состава происходит достаточно быстро. В уравнение гидростатического равновесия требуется внести слагаемое с радиальным ускорением, если радиус звезды быстро меняется, например, в случае радиальных пульсаций звезды. Также, если ядерные реакции неустойчивы или ядро звезды быстро коллапсирует, требуется добавить слагаемое с энтропией в уравнение для энергии.

Ссылки

• Kippenhahn, R. & Weigert, A. (1990), Stellar Structure and Evolution, Springer-Verlag 
• Hansen, Carl J.; Kawaler, Steven D. & Trimble, Virginia (2004), Stellar Interiors (2nd ed.), Springer, ISBN 0-387-20089-4 
• Kennedy, Dallas C. & Bludman, Sidney A. (1997), Variational Principles for Stellar Structure, Astrophysical Journal Т. 484 (1): 329, DOI 10.1086/304333 
• Weiss, Achim; Hillebrandt, Wolfgang; Thomas, Hans-Christoph & Ritter, H. (2004), Cox and Giuli's Principles of Stellar Structure, Cambridge Scientific Publishers 
• Zeilik, Michael A. & Gregory, Stephan A. (1998), Introductory Astronomy & Astrophysics (4th ed.), Saunders College Publishing, ISBN 0-03-006228-4