Список моментов инерции

Приведены формулы моме́нтов ине́рции для ряда массивных твёрдых тел различной формы. Момент инерции массы имеет размерность масса × длину². Он является аналогом массы при описании вращательного движения. Не следует путать его с моментом инерции плоских сечений^{[уточнить]}, который используется при расчетах изгибов.

Моменты инерции в таблице рассчитаны для постоянной плотности по всему объекту. Также предполагается, что ось вращения проходит через центр масс, если не указано иное.

Описание	Изображение	Моменты инерции	Комментарии
Тонкая цилиндрическая оболочка с открытыми концами радиуса r и массы m		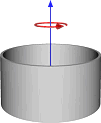[math]\displaystyle{ I = m r^2 }[/math]	Предполагается, что толщина корпуса пренебрежимо мала. Этот объект является частным случаем нижеследующего при r1=r2. Кроме того, точка массы m на конце стержня длиной r имеет тот же момент инерции, а r называется радиусом инерции.
Толстостенная цилиндрическая труба с открытыми концами, внутреннего радиуса r1, внешнего радиуса r2, длиной h и массой m		[math]\displaystyle{ I_z = \frac{1}{2} m\left({r_2}^2 + {r_1}^2\right) }[/math]   [math]\displaystyle{ I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right] }[/math] или при определении нормированной толщины tn = t/r и полагая r = r2, тогда [math]\displaystyle{ I_z = mr^2\left(1-t_n+\frac{1}{2}{t_n}^2\right) }[/math]	При плотности ρ и той же геометрии: [math]\displaystyle{ I_z = \frac{1}{2} \pi\rho h\left({r_2}^4 - {r_1}^4\right) }[/math]
Сплошной цилиндр радиуса r, высотой h и массы m		[math]\displaystyle{ I_z = \frac{m r^2}{2} }[/math]   [math]\displaystyle{ I_x = I_y = \frac{1}{12} m\left(3r^2+h^2\right) }[/math]	Это частный случай предыдущего объекта при r1=0. (Примечание: для правориентированной системы координат оси X-Y нужно поменять местами)
Тонкий твердый диск радиуса r и массы m		[math]\displaystyle{ I_z = \frac{m r^2}{2} }[/math] [math]\displaystyle{ I_x = I_y = \frac{m r^2}{4} }[/math]	Это частный случай предыдущего объекта при h=0.
Тонкое кольцо радиуса r и массы m		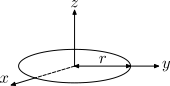[math]\displaystyle{ I_z = m r^2 }[/math] [math]\displaystyle{ I_x = I_y = \frac{m r^2}{2} }[/math]	Это частный случай тора при b=0 (см. ниже), а также частный случай толстостенной цилиндрической трубы с открытыми концами при r1=r2 и h=0.
Твёрдый шар радиуса r и массы m		[math]\displaystyle{ I = \frac{2 m r^2}{5} }[/math]	Шар можно представить как множество бесконечно тонких твёрдых дисков, радиус которых изменяется от 0 до r.
Пустотелая сфера радиуса r и массы m		[math]\displaystyle{ I = \frac{2 m r^2}{3} }[/math]	Аналогично твёрдой сфере, пустотелую сферу можно рассматривать как множество бесконечно тонких колец.
Твёрдый эллипсоид с полуосями a, b и c, с осью вращения a и массой m		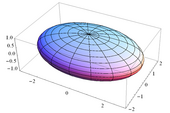[math]\displaystyle{ I_a = \frac{m (b^2+c^2)}{5} }[/math]	—
Прямой круговой конус радиуса r, высоты h и массы m		[math]\displaystyle{ I_z = \frac{3}{10}mr^2 }[/math]   [math]\displaystyle{ I_x = I_y = \frac{3}{5}m\left(\frac{r^2}{4}+h^2\right) }[/math]	—
Твёрдый кубоид с высотой h, шириной w, глубиной d и массой m		[math]\displaystyle{ I_h = \frac{1}{12} m\left(w^2+d^2\right) }[/math] [math]\displaystyle{ I_w = \frac{1}{12} m\left(h^2+d^2\right) }[/math] [math]\displaystyle{ I_d = \frac{1}{12} m\left(h^2+w^2\right) }[/math]	Для аналогично ориентированного куба с длиной ребра [math]\displaystyle{ s }[/math], [math]\displaystyle{ I_{CM} = \frac{m s^2}{6} }[/math].
Твёрдый кубоид с высотой D, шириной W, длиной L, массой m и с осью вращения вдоль самой длинной диагонали.		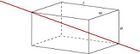[math]\displaystyle{ I = \frac{m\left(W^2D^2+L^2D^2+W^2L^2\right)}{6\left(L^2+W^2+D^2\right)} }[/math]	Для куба с длиной ребра [math]\displaystyle{ s }[/math], [math]\displaystyle{ I = \frac{m s^2}{6} }[/math].
Тонкая прямоугольная пластина высоты h, ширины w и массы m		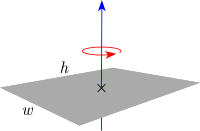[math]\displaystyle{ I_c = \frac {m(h^2 + w^2)}{12} }[/math]	—
Стержень длины L и массы m		[math]\displaystyle{ I_{\mathrm{center}} = \frac{m L^2}{12} }[/math]	Это выражение предполагает, что стержень имеет вид бесконечно тонкой, но жёсткой проволоки. Это частный случай предыдущего объекта для w = L и h = 0.
Тонкая прямоугольная пластина высоты h, ширины w и массы m (Ось вращения в конце пластины)		[math]\displaystyle{ I_e = \frac {m h^2}{3}+\frac {m w^2}{12} }[/math]	—
Стержень длины L и массы m (Ось вращения на конце стержня)		[math]\displaystyle{ I_{\mathrm{end}} = \frac{m L^2}{3} }[/math]	Это выражение предполагает, что стержень имеет вид бесконечно тонкой, но жёсткой проволоки. Это частный случай предыдущего объекта для h = L и w = 0.
Тороидальная труба радиуса a, радиуса сечения b и массы m.		Ось вращения относительно диаметра: [math]\displaystyle{ \frac{1}{8}\left(4a^2 + 5b^2\right)m }[/math]   Ось вращения относительно вертикальной оси: [math]\displaystyle{ \left(a^2 + \frac{3}{4}b^2\right)m }[/math]	—
Плоскость многоугольника с вершинами [math]\displaystyle{ \vec{P}_{1} }[/math], [math]\displaystyle{ \vec{P}_{2} }[/math], [math]\displaystyle{ \vec{P}_{3} }[/math], ..., [math]\displaystyle{ \vec{P}_{N} }[/math] и массой [math]\displaystyle{ m }[/math], равномерно распределенной на его объёму, вращающийся относительно оси, перпендикулярной плоскости и проходящей через начало координат.		[math]\displaystyle{ I=\frac{m}{6}\frac{\sum\limits_{n=1}^{N-1}\|\vec{P}_{n+1}\times\vec{P}_{n}\|(\vec{P}^{2}_{n+1}+\vec{P}_{n+1}\cdot\vec{P}_{n}+\vec{P}_{n}^{2})}{\sum\limits_{n=1}^{N-1}\|\vec{P}_{n+1}\times\vec{P}_{n}\|} }[/math]	—
Бесконечный диск с нормально распределенной вокруг осей вращения массой по двум координатам (т.е. [math]\displaystyle{ \rho(x,y) = \tfrac{m}{2\pi ab}\, e^{-((x/a)^2+(y/b)^2)/2} }[/math] где: [math]\displaystyle{ \rho(x,y) }[/math] — плотность масс как функция x и y).		[math]\displaystyle{ I = m (a^2+b^2) }[/math]
Две точечные массы M и m на расстоянии x друг от друга		[math]\displaystyle{ I = \frac{ M m }{ M \! + \! m } x^2 = \mu x^2 }[/math]	[math]\displaystyle{ \mu }[/math] — приведённая масса.

См. также

• Теорема Штейнера