Ридберговские атомы
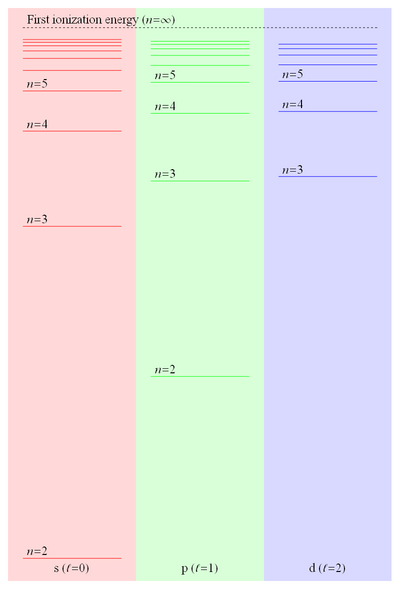
Ри́дберговские а́томы (названы в честь Й. Р. Ридберга) — водородоподобные атомы и атомы щелочных металлов, у которых внешний электрон находится в высоковозбуждённом состоянии (вплоть до уровней n порядка 1000). Для перевода атома из основного в возбуждённое состояние его облучают резонансным лазерным светом или инициируют радиочастотный разряд. Размер ридберговского атома может превышать размер находящегося в основном состоянии того же самого атома почти в 106 раз для n = 1000.
Свойства ридберговских атомов
Электрон, вращающийся на орбите радиуса r вокруг ядра, по второму закону Ньютона испытывает силу
- [math]\displaystyle{ \mathbf{F} = m\mathbf{a} \Rightarrow \frac{ke^2}{r^2} = \frac{mv^2}{r}, }[/math]
где [math]\displaystyle{ k = 1 / (4 \pi \epsilon_0) }[/math] ([math]\displaystyle{ \epsilon_0 }[/math] — диэлектрическая восприимчивость), e — заряд электрона.
Орбитальный момент в единицах ħ равен
- [math]\displaystyle{ mvr = n\hbar. }[/math]
Из этих двух уравнений получим выражение для орбитального радиуса электрона, находящегося в состоянии n:
- [math]\displaystyle{ r = \frac{n^2\hbar^2}{ke^2m}. }[/math]
Энергия связи такого водородоподобного атома равна
- [math]\displaystyle{ W_n = \frac{\mathrm{Ry}}{(n - \delta)^2}, }[/math]
где Ry = 13,6 эВ есть постоянная Ридберга, а δ — дефект заряда ядра, который при больших n несущественен. Разница энергий между n-м и (n + 1)-м уровнями энергии равна
- [math]\displaystyle{ \Delta W \equiv W_n - W_{n+1} \approx \frac{\mathrm{Ry}}{n^3}. }[/math]
Характерный размер атома rn и типичный квазиклассический период обращения электрона равны
- [math]\displaystyle{ r_n \approx a_\text{B} n^2, \quad T_n \approx T_1 n^3, }[/math]
где aB = 0,5⋅10−10 м — боровский радиус, а T1 ~ 10−16 с.
| Главное квантовое число, [math]\displaystyle{ n }[/math] | Первое возбуждённое состояние, [math]\displaystyle{ n = 2 }[/math] |
Ридберговское состояние, [math]\displaystyle{ n = 1000 }[/math] |
|---|---|---|
| Энергия связи электрона в атоме (потенциал ионизации), эВ | ≃ 5 | ≃ 10−5 |
| Размер атома (радиус орбиты электрона), м | ~ 10−10 | ~ 10−4 |
| Период обращения электрона по орбите, с | ~ 10−16 | ~ 10−7 |
| Естественное время жизни, с | ~ 10−8 | ~ 1 |
Длина волны излучения атома водорода при переходе с n′ = 91 на n = 90 равна 3,4 см[1].
Дипольная блокада ридберговских атомов
При возбуждении атомов из основного состояния в ридберговское происходит интересное явление, получившие название «дипольная блокада».
В разреженном атомном паре расстояние между атомами, находящимися в основном состоянии, велико, и взаимодействия между атомами практически нет. Однако, при возбуждении атомов в ридберговское состояние их радиус орбиты увеличивается в [math]\displaystyle{ n^2 }[/math] и достигает величины порядка 1 мкм. В результате атомы «сближаются», взаимодействие между ними значительно увеличивается, что вызывает смещение энергии состояний атомов. К чему это приводит? Предположим, что слабым импульсом света удалось возбудить только один атом из основного в ридберговское состояние. Попытка заселить тот же уровень другим атомом из-за «дипольной блокады» становится заведомо невозможной, так как ридберговское состояние второго атома из-за взаимодействия с первым атомом изменит энергию и, следовательно, будет «вне» резонанса с частотой фотона.[2].
Когерентное управление дипольной блокадой ридберговских атомов лазерным светом делает их перспективным кандидатом для практической реализации квантового компьютера.[3] По сообщениям научной печати, до 2009 года важный для вычислений элемент квантового компьютера двух-кубитный вентиль экспериментально не был реализован. Однако, имеются сообщения о наблюдении коллективного возбуждения и динамического взаимодействия между двумя атомами[4][5] и в мезоскопических образцах[2].
Сильно взаимодействующие ридберговские атомы характеризуются квантовым критическим поведением, что обеспечивает фундаментальный научный интерес к ним независимо от приложений[6].
Направления исследования и возможные применения
Исследования, связанные с ридберговскими состояниями атомов, можно условно разбить на две группы: изучение самих атомов и использование их свойств для прочих целей.
Фундаментальные направления исследования:
- Из нескольких состояний с большими n можно составить волновой пакет, который будет более-менее локализован в пространстве. Если при этом большим будет и орбитальное квантовое число, то мы получим почти классическую картинку: локализованное электронное облако вращается вокруг ядра на большом расстоянии от него.
- Если орбитальный момент мал, то движение такого волнового пакета будет квазиодномерным: электронное облако будет удаляться от ядра и снова приближаться к нему. Это аналог сильно вытянутой эллиптической орбиты в классической механике при движении вокруг Солнца.
- Поведение ридберговского электрона во внешних электрических и магнитных полях. Обычные электроны, находящиеся близко к ядру, в основном чувствуют сильное электростатическое поле ядра (порядка 109 В/см), а внешние поля для них играют роль лишь мелких добавок. Ридберговский электрон чувствует сильно ослабленное поле ядра (порядка E0 / n4), и потому внешние поля могут кардинально изменить движение электрона.
- Интересными свойствами обладают атомы с двумя ридберговскими электронами, причем один электрон «крутится» вокруг ядра на большем расстоянии, чем другой. Такие атомы называются планетарными.
- По одной из гипотез, из ридберговского вещества состоит шаровая молния[7].
В 2009 году исследователями из университета Штутгарта удалось получить ридберговскую молекулу[англ.][8].
Радиоастрономия
Первые экспериментальные данные по ридберговским атомам в радиоастрономии были получены в 1964 году Р. С. Сороченко и др. (ФИАН) на 22-метровом зеркальном радиотелескопе, созданном для исследования излучения космических объектов в сантиметровом диапазоне частот. При ориентации телескопа на туманность Омега в спектре радиоизлучения, идущего от этой туманности, была обнаружена линия излучения на длине волны λ ≃ 3,4 см. Эта длина волны соответствует переходу между ридберговскими состояниями ń = 91 и n = 90 в спектре атома водорода[1].
Примечания
- ↑ 1,0 1,1 1,2 Делоне Н. Б. Ридберговские атомы // Соросовский образовательный журнал, 1998, № 4, с. 64-70
- ↑ 2,0 2,1 R. Heidemann et al. Evidence for Coherent Collective Rydberg Excitation in the Strong Blockade Regime (англ.) // Physical Review Letters : journal. — 2007. — Vol. 99, no. 16. — P. 163601. — doi:10.1103/PhysRevLett.99.163601.
- ↑ D. Jaksch; J. I. Cirac; P. Zoller; S. L. Rolston; R. Côté; M. D. Lukin. Fast Quantum Gates for Neutral Atoms (англ.) // Physical Review Letters : journal. — 2000. — Vol. 85, no. 10. — P. 2208—2211. — doi:10.1103/PhysRevLett.85.2208. — . — arXiv:quant-ph/0004038. — PMID 10970499.
- ↑ A. Gaetan; Miroshnychenko, Yevhen; Wilk, Tatjana; Chotia, Amodsen; Viteau, Matthieu; Comparat, Daniel; Pillet, Pierre; Browaeys, Antoine; Grangier, Philippe. Observation of collective excitation of two individual atoms in the Rydberg blockade regime (англ.) // Nature Physics : journal. — 2009. — Vol. 5, no. 2. — P. 115—118. — doi:10.1038/nphys1183. — . — arXiv:0810.2960.
- ↑ E. Urban; Johnson, T. A.; Henage, T.; Isenhower, L.; Yavuz, D. D.; Walker, T. G.; Saffman, M. Observation of Rydberg blockade between two atoms (англ.) // Nature Physics : journal. — 2009. — Vol. 5, no. 2. — P. 110—114. — doi:10.1038/nphys1178. — . — arXiv:0805.0758.
- ↑ H. Weimer; Low, Robert; Pfau, Tilman; Buchler, Hans Peter. Quantum Critical Behavior in Strongly Interacting Rydberg Gases (англ.) // Physical Review Letters : journal. — 2008. — Vol. 101, no. 25. — P. 250601. — doi:10.1103/PhysRevLett.101.250601. — . — arXiv:0806.3754. — PMID 19113686.
- ↑ Cohesion in ball lightning (недоступная ссылка)
- ↑ membrana.ru «Впервые в мире получена молекула Ридберга» (недоступная ссылка). Дата обращения: 24 апреля 2009. Архивировано 24 сентября 2010 года.
Литература
- Neukamner J., Rinenberg H., Vietzke К. et al. Spectroscopy of Rydberg Atoms at n ≅ 500 // Phys. Rev. Lett. 1987. Vol. 59. P. 26.
- Frey M. T. Hill S.B.. Smith K.A.. Dunning F.B., Fabrikant I.I. Studies of Electron-Molecule Scattering at Microelectronvolt Energies Using Very-High-n Rydberg Atoms // Phys. Rev. Lett. 1995. Vol. 75, № 5. P. 810—813.
- Сороченко Р. Л., Саломонович A.E. Гигантские атомы в космосе // Природа. 1987. № 11. С. 82.
- Далгарно А. Ридберговские атомы в астрофизике // Ридберговские состояния атомов и молекул: Пер. с англ. / Под ред. Р. Стеббинса, Ф. Даннинга. М.: Мир, 1985. С. 9.
- Смирнов Б. М. Возбуждённые атомы. М.: Энергоиздат, 1982. Гл. 6.
Ссылки
- Делоне Н. Б. Ридберговские атомы // Соросовский образовательный журнал, 1998, № 4, с. 64-70
- «Конденсированное ридберговское вещество», Э. А. Маныкин, М. И. Ожован, П. П. Полуэктов, статья из журнала «Природа» N1, 2001.
- Rydberg Physics, Nikola Šibalić and Charles S Adams, IOP Publishing (2018)