Разделение секрета

Разделение секрета (англ. secret sharing) — термин в криптографии, под которым понимают любой из способов распределения секрета среди группы участников, каждому из которых достаётся своя некая доля. Секрет может воссоздать только коалиция участников из первоначальной группы, причём входить в коалицию должно не менее некоторого изначально известного их числа.
Схемы разделения секрета применяются в случаях, когда существует значимая вероятность компрометации одного или нескольких хранителей секрета, но вероятность недобросовестного сговора значительной части участников считается пренебрежимо малой.
Существующие схемы имеют две составляющие: разделение и восстановление секрета. К разделению относится формирование частей секрета и распределение их между членами группы, что позволяет разделить ответственность за секрет между её участниками. Обратная схема должна обеспечить его восстановление при условии доступности его хранителей в некотором необходимом количестве[1].
Пример использования: протокол тайного голосования на основе разделения секрета[2].
Простейший пример схемы разделения секрета
Пусть имеется группа из [math]\displaystyle{ t }[/math] человек и сообщение [math]\displaystyle{ s }[/math] длины [math]\displaystyle{ n }[/math], состоящее из двоичных символов. Если подобрать случайным образом такие двоичные сообщения [math]\displaystyle{ s_1, \ldots, s_t }[/math], что в сумме они будут равняться [math]\displaystyle{ s }[/math], и распределить эти сообщения между всеми членами группы, получится, что прочесть сообщение будет возможно только в случае, если все члены группы соберутся вместе[1].
В такой схеме есть существенная проблема: в случае утраты хотя бы одного из членов группы, секрет будет утерян для всей группы безвозвратно.
Пороговая схема
В отличие от процедуры разбиения секрета, где [math]\displaystyle{ t=n }[/math], в процедуре разделения секрета количество долей, которые нужны для восстановления секрета, может отличаться от того, на сколько долей секрет разделён. Такая схема носит названия пороговой схемы [math]\displaystyle{ \left( t, n \right) }[/math], где [math]\displaystyle{ n }[/math] — количество долей, на которые был разделён секрет, а [math]\displaystyle{ t }[/math] — количество долей, которые нужны для восстановления секрета. Идеи схем [math]\displaystyle{ t \neq n }[/math] были независимо предложены в 1979 году Ади Шамиром и Джорджем Блэкли. Кроме этого, подобные процедуры исследовались Гусом Симмонсом[3][4][5].
Если коалиция участников такова, что они имеют достаточное количество долей для восстановления секрета, то коалиция называется разрешённой. Схемы разделения секрета, в которых разрешённые коалиции участников могут однозначно восстановить секрет, а неразрешённые не получают никакой апостериорной информации о возможном значении секрета, называются совершенными[6].
Схема Шамира
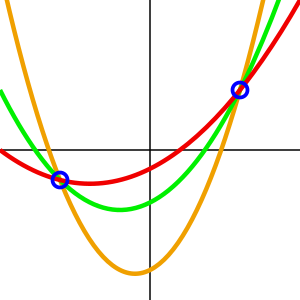
Идея схемы заключается в том, что двух точек достаточно для задания прямой, трех точек — для задания параболы, четырёх точек — для кубической параболы, и так далее. Чтобы задать многочлен степени [math]\displaystyle{ k }[/math], требуется [math]\displaystyle{ k+1 }[/math] точек.
Для того, чтобы после разделения секрет могли восстановить только [math]\displaystyle{ k }[/math] участников, его «прячут» в формулу многочлена степени [math]\displaystyle{ (k-1) }[/math] над конечным полем [math]\displaystyle{ G }[/math]. Для однозначного восстановления этого многочлена необходимо знать его значения в [math]\displaystyle{ k }[/math] точках, причем, используя меньшее число точек, однозначно восстановить исходный многочлен не получится. Количество же различных точек многочлена не ограничено (на практике оно ограничивается размером числового поля [math]\displaystyle{ G }[/math], в котором ведутся расчёты).
Кратко данный алгоритм можно описать следующим образом. Пусть дано конечное поле [math]\displaystyle{ G }[/math]. Зафиксируем [math]\displaystyle{ n }[/math] различных ненулевых несекретных элементов данного поля. Каждый из этих элементов приписывается определённому члену группы. Далее выбирается произвольный набор из [math]\displaystyle{ t }[/math] элементов поля [math]\displaystyle{ G }[/math], из которых составляется многочлен [math]\displaystyle{ f(x) }[/math] над полем [math]\displaystyle{ G }[/math] степени [math]\displaystyle{ t-1, 1\lt t\leq n }[/math]. После получения многочлена вычисляем его значение в несекретных точках и сообщаем полученные результаты соответствующим членам группы[1].
Чтобы восстановить секрет, можно воспользоваться интерполяционной формулой, например формулой Лагранжа.
Важным достоинством схемы Шамира является то, что она легко масштабируема[5]. Чтобы увеличить число пользователей в группе, необходимо лишь добавить соответствующее число несекретных элементов к уже существующим, при этом должно выполняться условие [math]\displaystyle{ r_i\neq r_j }[/math] при [math]\displaystyle{ i\neq j }[/math]. В то же время, компрометация одной части секрета переводит схему из [math]\displaystyle{ (n,t) }[/math]-пороговой в [math]\displaystyle{ (n-1,t-1) }[/math]-пороговую.
Схема Блэкли
Две непараллельные прямые на плоскости пересекаются в одной точке. Любые две некомпланарные плоскости пересекаются по одной прямой, а три некомпланарные плоскости в пространстве пересекаются тоже в одной точке. Вообще n n-мерных гиперплоскостей всегда пересекаются в одной точке. Одна из координат этой точки будет секретом. Если закодировать секрет как несколько координат точки, то уже по одной доле секрета (одной гиперплоскости) можно будет получить какую-то информацию о секрете, то есть о взаимозависимости координат точки пересечения.

|

|

|
| Схема Блэкли в трёх измерениях: каждая доля секрета — это плоскость, а секрет — это одна из координат точки пересечения плоскостей. Двух плоскостей недостаточно для определения точки пересечения. | ||
С помощью схемы Блэкли[4] можно создать (t, n)-схему разделения секрета для любых t и n: для этого надо использовать размерность пространства, равную t, и каждому из n игроков дать одну гиперплоскость, проходящую через секретную точку. Тогда любые t из n гиперплоскостей будут однозначно пересекаться в секретной точке.
Схема Блэкли менее эффективна, чем схема Шамира: в схеме Шамира каждая доля такого же размера, как и секрет, а в схеме Блэкли каждая доля в t раз больше. Существуют улучшения схемы Блэкли, позволяющие повысить её эффективность.
Схемы, основанные на китайской теореме об остатках
В 1983 году Морис Миньотт[англ.], Асмут и Блум предложили две схемы разделения секрета, основанные на китайской теореме об остатках. Для некоторого числа (в схеме Миньотта это сам секрет, в схеме Асмута — Блума — некоторое производное число) вычисляются остатки от деления на последовательность чисел, которые раздаются сторонам. Благодаря ограничениям на последовательность чисел, восстановить секрет может только определённое число сторон[7][8].
Пусть количество пользователей в группе равно [math]\displaystyle{ n }[/math]. В схеме Миньотта выбирается некоторое множество попарно взаимно простых чисел [math]\displaystyle{ \{m_1,m_2,...,m_n\} }[/math] таких, что произведение [math]\displaystyle{ k-1 }[/math] наибольших чисел меньше, чем произведение [math]\displaystyle{ k }[/math] наименьших из этих чисел. Пусть эти произведения равны [math]\displaystyle{ M }[/math] и [math]\displaystyle{ N }[/math], соответственно. Число [math]\displaystyle{ k }[/math] называется порогом для конструируемой схемы по множеству [math]\displaystyle{ \{m_1,m_2,...,m_n\} }[/math]. В качестве секрета выбирается число [math]\displaystyle{ S }[/math] такое, для которого выполняется соотношение [math]\displaystyle{ M\lt S\lt N }[/math]. Части секрета распределяются между участниками группы следующим образом: каждому участнику выдается пара чисел [math]\displaystyle{ (r_i,m_i) }[/math], где [math]\displaystyle{ r_i\equiv S\pmod{m_i} }[/math].
Чтобы восстановить секрет, необходимо объединить [math]\displaystyle{ t\geq k }[/math] фрагментов. В этом случае получим систему сравнений вида [math]\displaystyle{ x\equiv r_i\pmod{m_i} }[/math], множество решений которой можно найти, используя китайскую теорему об остатках. Секретное число [math]\displaystyle{ S }[/math] принадлежит этому множеству и удовлетворяет условию [math]\displaystyle{ S\lt m_1\cdot m_2\cdot...\cdot m_t }[/math]. Также несложно показать, что если число фрагментов меньше [math]\displaystyle{ k }[/math], то, чтобы найти секрет [math]\displaystyle{ S }[/math], необходимо перебрать порядка [math]\displaystyle{ \frac{N}{M} }[/math] целых чисел. При правильном выборе чисел [math]\displaystyle{ m_i }[/math] такой перебор практически невозможно реализовать. К примеру, если разрядность [math]\displaystyle{ m_i }[/math] будет от 129 до 130 бит, а [math]\displaystyle{ k\lt 15 }[/math], то соотношение [math]\displaystyle{ \frac{N}{M} }[/math] будет иметь порядок [math]\displaystyle{ 2^{100} }[/math][9].
Схема Асмута — Блума является доработанной схемой Миньотта. В отличие от схемы Миньотта, её можно построить в таком виде, чтобы она была совершенной[10].
Схемы, основанные на решении систем уравнений
В 1983 году Карнин, Грин и Хеллман предложили свою схему разделения секрета, которая основывалась на невозможности решить систему с [math]\displaystyle{ m }[/math] неизвестными, имея менее [math]\displaystyle{ m }[/math] уравнений[11].
В рамках данной схемы выбираются [math]\displaystyle{ n+1 }[/math] [math]\displaystyle{ m }[/math]-мерных векторов [math]\displaystyle{ V_0, V_1, ..., V_n }[/math] так, чтобы любая матрица размером [math]\displaystyle{ m\times m }[/math], составленная из этих векторов, имела ранг [math]\displaystyle{ m }[/math]. Пусть вектор [math]\displaystyle{ U }[/math] имеет размерность [math]\displaystyle{ m }[/math].
Секретом в схеме является матричное произведение [math]\displaystyle{ U^T V_0 }[/math]. Долями секрета являются произведения [math]\displaystyle{ U^T V_i, 1 \leq i \leq n }[/math].
Имея любые [math]\displaystyle{ m }[/math] долей, можно составить систему линейных уравнений размерности [math]\displaystyle{ m\times m }[/math], неизвестными в которой являются коэффициенты [math]\displaystyle{ U }[/math]. Решив данную систему, можно найти [math]\displaystyle{ U }[/math], а имея [math]\displaystyle{ U }[/math], можно найти секрет. При этом система уравнений не имеет решения в случае, если долей меньше, чем [math]\displaystyle{ m }[/math][12].
Способы обмана пороговой схемы
Существуют несколько способов нарушить протокол работы пороговой схемы:
- владелец одной из долей может помешать восстановлению общего секрета, отдав в нужный момент неверную (случайную) долю[13].
- злоумышленник, не имея доли, может присутствовать при восстановлении секрета. Дождавшись оглашения нужного числа долей, он быстро восстанавливает секрет самостоятельно и генерирует ещё одну долю, после чего предъявляет её остальным участникам. В результате он получает доступ к секрету и остаётся непойманным[14].
Также существуют другие возможности нарушения работы, не связанные с особенностями реализации схемы:
- злоумышленник может сымитировать ситуацию, при которой необходимо раскрытие секрета, тем самым выведав доли участников[14].
См. также
Примечания
- ↑ Перейти обратно: 1,0 1,1 1,2 Алферов, Зубов, Кузьмин и др., 2002, с. 401.
- ↑ Schoenmakers, 1999.
- ↑ C. J. Simmons. An introduction to shared secret and/or shared control schemes and their application (англ.) // Contemporary Cryptology. — IEEE Press, 1991. — P. 441—497.
- ↑ Перейти обратно: 4,0 4,1 Blakley, 1979.
- ↑ Перейти обратно: 5,0 5,1 Shamir, 1979.
- ↑ Блэкли, Кабатянский, 1997.
- ↑ Mignotte, 1982.
- ↑ Asmuth, Bloom, 1983.
- ↑ Молдовян, Молдовян, 2005, с. 225.
- ↑ Шенец, 2011.
- ↑ Karnin, Greene, Hellman, 1983.
- ↑ Шнайер Б. Прикладная криптография. — 2-е изд. — Триумф, 2002. — С. 590. — 816 с. — ISBN 5-89392-055-4.
- ↑ Pasailă, Alexa, Iftene, 2010.
- ↑ Перейти обратно: 14,0 14,1 Шнайер, 2002, с. 69.
Литература
- Шнайер Б. 3.7. Разделение секрета // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 93—96. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.
- Шнайер Б. 23.2 Алгоритмы разделения секрета // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 588—591. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.