Пространство состояний (теория управления)

Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение её состояний.

Определение

Пространство состояний обычно называют фазовым пространством динамической системы, а траекторию движения изображающей точки в этом пространстве — фазовой траекторией.

В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями. Кроме того, в пространстве состояний относительно просто работать с MIMO-системами.

Линейные непрерывные системы

Структурная схема непрерывной линейной системы, описанной в виде переменных состояния

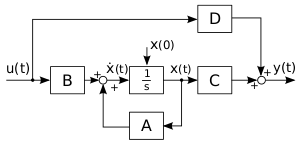
Для случая линейной системы с [math]\displaystyle{ p }[/math] входами, [math]\displaystyle{ q }[/math] выходами и [math]\displaystyle{ n }[/math] переменными состояния описание имеет вид:

[math]\displaystyle{ \dot{\mathbf{x}}(t) = A(t) \mathbf{x}(t) + B(t) \mathbf{u}(t) }[/math]

[math]\displaystyle{ \mathbf{y}(t) = C(t) \mathbf{x}(t) + D(t) \mathbf{u}(t) }[/math]

где

[math]\displaystyle{ x(t) \in \mathbb{R}^n }[/math]; [math]\displaystyle{ y(t) \in \mathbb{R}^q }[/math]; [math]\displaystyle{ u(t) \in \mathbb{R}^p }[/math];

[math]\displaystyle{ \operatorname{dim}[A(\cdot)] = n \times n }[/math], [math]\displaystyle{ \operatorname{dim}[B(\cdot)] = n \times p }[/math], [math]\displaystyle{ \operatorname{dim}[C(\cdot)] = q \times n }[/math], [math]\displaystyle{ \operatorname{dim}[D(\cdot)] = q \times p }[/math], [math]\displaystyle{ \dot{\mathbf{x}}(t) := {d\mathbf{x}(t) \over dt} }[/math]:

[math]\displaystyle{ x(\cdot) }[/math] — вектор состояния, элементы которого называются состояниями системы

[math]\displaystyle{ y(\cdot) }[/math] — вектор выхода,

[math]\displaystyle{ u(\cdot) }[/math] — вектор управления,

[math]\displaystyle{ A(\cdot) }[/math] — матрица системы,

[math]\displaystyle{ B(\cdot) }[/math] — матрица управления,

[math]\displaystyle{ C(\cdot) }[/math] — матрица выхода,

[math]\displaystyle{ D(\cdot) }[/math] — матрица прямой связи.

Часто матрица [math]\displaystyle{ D(\cdot) }[/math] является нулевой, это означает, что в системе нет явной прямой связи.

Дискретные системы

Для дискретных систем запись уравнений в пространстве основывается не на дифференциальных, а на разностных уравнениях:

[math]\displaystyle{ \mathbf{x}(nT + T) = A(nT) \mathbf{x}(nT) + B(nT) \mathbf{u}(nT) }[/math]

[math]\displaystyle{ \mathbf{y}(nT) = C(nT) \mathbf{x}(nT) + D(nT) \mathbf{u}(nT) }[/math]

Нелинейные системы

Нелинейная динамическая система n-го порядка может быть описана в виде системы из n уравнений 1-го порядка:

[math]\displaystyle{ \dot x_1=f_1(x_1(t);\ldots,x_n(t),u_1(t),\ldots,u_m(t)) }[/math]

[math]\displaystyle{ \vdots }[/math]

[math]\displaystyle{ \dot x_n=f_n(x_1(t);\ldots,x_n(t),u_1(t),\ldots,u_m(t)) }[/math]

или в более компактной форме:

[math]\displaystyle{ \mathbf{\dot{x}}(t) = \mathbf{f}(t, \mathbf{x}(t),\mathbf{u}(t)) }[/math]

[math]\displaystyle{ \mathbf{y}(t) = \mathbf{h}(t, \mathbf{x}(t),\mathbf{u}(t)) }[/math].

Первое уравнение — это уравнение состояния, второе — уравнение выхода.

Линеаризация

В некоторых случаях возможна линеаризация описания динамической системы для окрестности рабочей точки [math]\displaystyle{ (\mathbf{\tilde x}, \mathbf{\tilde u}) }[/math]. В установившемся режиме [math]\displaystyle{ (\mathbf{\tilde u}= const) }[/math] для рабочей точки [math]\displaystyle{ \mathbf{\tilde x}= const, }[/math] справедливо следующее выражение:

[math]\displaystyle{ \mathbf{\dot{x}} = \mathbf{f}(\mathbf{\tilde x},\mathbf{\tilde u})=\mathbf{0} }[/math]

Вводя обозначения:

[math]\displaystyle{ \delta\mathbf{u} = \mathbf{u}-\mathbf{\tilde u} }[/math]

[math]\displaystyle{ \delta\mathbf{x} = \mathbf{x}-\mathbf{\tilde x} }[/math]

Разложение уравнения состояния [math]\displaystyle{ \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)) }[/math] в ряд Тейлора, ограниченное первыми двумя членами даёт следующее выражение:

[math]\displaystyle{ \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t))\approx \mathbf{f}(\mathbf{\tilde x}(t),\mathbf{\tilde u}(t)) + \frac{\delta \mathbf{f}}{\delta \mathbf{x}} \delta \mathbf{x} + \frac{\delta \mathbf{f}}{\delta \mathbf{u}} \delta \mathbf{u} }[/math]

При взятии частных производных вектор-функции [math]\displaystyle{ \mathbf{f} }[/math] по вектору переменных состояний [math]\displaystyle{ \mathbf{x} }[/math] и вектору входных воздействий [math]\displaystyle{ \mathbf{u} }[/math] получаются матрицы Якоби соответствующих систем функций:

[math]\displaystyle{ \frac{\delta \mathbf{f}}{\delta \mathbf{x}} = \begin{bmatrix} \frac{\delta \mathbf{f_1}}{\delta \mathbf{x_1}}& \cdots & \frac{\delta \mathbf{f_1}}{\delta \mathbf{x_n}} \\ \vdots & \ddots & \vdots \\ \frac{\delta \mathbf{f_n}}{\delta \mathbf{x_1}}& \cdots & \frac{\delta \mathbf{f_n}}{\delta \mathbf{x_n}} \end{bmatrix} \quad \frac{\delta \mathbf{f}}{\delta \mathbf{u}} = \begin{bmatrix} \frac{\delta \mathbf{f_1}}{\delta \mathbf{u_1}}& \cdots & \frac{\delta \mathbf{f_1}}{\delta \mathbf{u_p}} \\ \vdots & \ddots & \vdots \\ \frac{\delta \mathbf{f_n}}{\delta \mathbf{u_1}}& \cdots & \frac{\delta \mathbf{f_n}}{\delta \mathbf{u_p}} \end{bmatrix} }[/math].

Аналогично для функции выхода:

[math]\displaystyle{ \frac{\delta \mathbf{h}}{\delta \mathbf{x}} = \begin{bmatrix} \frac{\delta \mathbf{h_1}}{\delta \mathbf{x_1}}& \cdots & \frac{\delta \mathbf{h_1}}{\delta \mathbf{x_n}} \\ \vdots & \ddots & \vdots \\ \frac{\delta \mathbf{h_q}}{\delta \mathbf{x_1}}& \cdots & \frac{\delta \mathbf{h_q}}{\delta \mathbf{x_n}} \end{bmatrix} \quad \frac{\delta \mathbf{h}}{\delta \mathbf{u}} = \begin{bmatrix} \frac{\delta \mathbf{h_1}}{\delta \mathbf{u_1}}& \cdots & \frac{\delta \mathbf{h_1}}{\delta \mathbf{u_p}} \\ \vdots & \ddots & \vdots \\ \frac{\delta \mathbf{h_q}}{\delta \mathbf{u_1}}& \cdots & \frac{\delta \mathbf{h_q}}{\delta \mathbf{u_p}} \end{bmatrix} }[/math]

Учитывая [math]\displaystyle{ \delta \mathbf{\dot x}=\mathbf{\dot x}-\mathbf{\dot \tilde x}=\mathbf{\dot x} }[/math], линеаризованное описание динамической системы в окрестности рабочей точки примет вид:

[math]\displaystyle{ \mathbf{\dot x} }[/math]	[math]\displaystyle{ =\mathbf{A}\delta \mathbf{x}+\mathbf{B} \delta \mathbf{u} }[/math]
[math]\displaystyle{ \delta \mathbf{y} }[/math]	[math]\displaystyle{ =\mathbf{C}\delta \mathbf{x}+\mathbf{D} \delta \mathbf{u} }[/math]

где

[math]\displaystyle{ \mathbf{A}=\frac{\delta \mathbf{f}}{\delta \mathbf{x}}\quad \mathbf{B}=\frac{\delta \mathbf{f}}{\delta \mathbf{u}}\quad \mathbf{C}=\frac{\delta \mathbf{h}}{\delta \mathbf{x}}\quad \mathbf{D}=\frac{\delta \mathbf{h}}{\delta \mathbf{u}} }[/math].

Примеры

Модель в пространстве состояний для маятника

Маятник является классической свободной нелинейной системой. Математически движение маятника описывается следующим соотношением:

[math]\displaystyle{ ml\ddot\theta(t)= -mg\sin\theta(t) - kl\dot\theta(t) }[/math]

где

• [math]\displaystyle{ \theta(t) }[/math] — угол отклонения маятника.
• [math]\displaystyle{ m }[/math] — приведённая масса маятника
• [math]\displaystyle{ g }[/math] — ускорение свободного падения
• [math]\displaystyle{ k }[/math] — коэффициент трения в подшипнике подвеса
• [math]\displaystyle{ l }[/math] — длина подвеса маятника

В таком случае уравнения в пространстве состояний будут иметь вид:

[math]\displaystyle{ \dot{x_1}(t) = x_2(t) }[/math]

[math]\displaystyle{ \dot{x_2}(t) = - \frac{g}{l}\sin{x_1}(t) - \frac{k}{m}{x_2}(t) }[/math]

где

• [math]\displaystyle{ x_1(t):=\theta(t) }[/math] — угол отклонения маятника
• [math]\displaystyle{ x_2(t) :=\dot{x_1}(t) }[/math] — угловая скорость маятника
• [math]\displaystyle{ \dot{x_2}(t) :=\ddot{x_1}(t) }[/math] — угловое ускорение маятника

Запись уравнений состояния в общем виде:

[math]\displaystyle{ \dot{\mathbf{x}}(t) = \left( \begin{matrix} \dot{x_1}(t) \\ \dot{x_2}(t) \end{matrix} \right) = \mathbf{f}(t, x(t)) = \left( \begin{matrix} x_2(t) \\ - \frac{g}{l}\sin{x_1}(t) - \frac{k}{m}{x_2}(t) \end{matrix} \right) }[/math].

Линеаризация модели маятника

Линеаризованная матрица системы для модели маятника в окрестности точки равновесия [math]\displaystyle{ \left(\tilde x_1=0 \right) }[/math] имеет вид:

[math]\displaystyle{ \frac{\delta \mathbf{f}}{\delta \mathbf{x}} = \left( \begin{matrix} 0&\ 1 \\ -\frac{g}{l}\cos{\tilde x_1}&\ - \frac{k}{m} \end{matrix} \right) = \left( \begin{matrix} 0&\ 1 \\ -\frac{g}{l}&\ - \frac{k}{m} \end{matrix} \right) }[/math]

При отсутствии трения в подвесе (k = 0) получим уравнение движения математического маятника:

[math]\displaystyle{ \ddot x = -\frac{g}{l}x }[/math]

См. также

• Теория управления
• Фазовое пространство
• Критерий устойчивости в пространстве состояний
• Пространство понятий
• Система отсчёта
• Модальное управление

Литература

• Книги

• Статьи

Ссылки

• Исходные дифференциальные уравнения САР