Односвязное пространство
Внешний вид

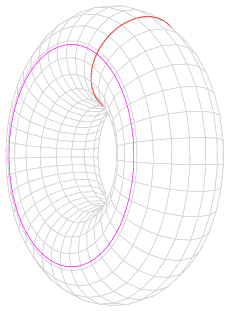
Односвязное пространство — линейно связное топологическое пространство, в котором любой замкнутый путь можно непрерывно стянуть в точку. Пример: сфера односвязна, а поверхность тора не односвязна, потому что окружности на торе, показанные красным на рисунке, нельзя стянуть в точку.
Определения
- Линейно связное топологическое пространство [math]\displaystyle{ X }[/math] называется односвязным, если все замкнутые пути в нём гомотопны нулю.
- Эквивалентное определение: Линейно связное топологическое пространство [math]\displaystyle{ X }[/math] называется односвязным, если фундаментальная группа пространства [math]\displaystyle{ X }[/math] тривиальна.
Примеры
- Любое выпуклое множество в евклидовом пространстве односвязно.
- Круговое кольцо, лента Мёбиуса, проективная плоскость не односвязны.
Свойства
Односвязность является гомотопическим инвариантом, то есть гомотопически эквивалентные пространства либо оба односвязны, либо оба не односвязны.
Литература
- Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
Ссылки
- И. М. Виноградов. Односвязная область // Математическая энциклопедия. — М.: Советская энциклопедия. — 1977—1985.
В статье не хватает ссылок на источники (см. также рекомендации по поиску). |