Многомерное время в физике

Эта статья — о многомерном времени в физике. О многомерном времени в физике, философии и фантастике см. многомерное время.

Свойства S+T-мерного пространства-времени по Максу Тегмарку

Специальная теория относительности (СТО) описывает пространство-время в виде псевдориманова многообразия с одним отрицательным собственным значением метрического тензора, которое соответствует «временноподобному» направлению. Метрика с несколькими отрицательными собственными значениями будет соответственно подразумевать наличие нескольких временных направлений, то есть время будет многомерным, но в настоящее время нет консенсуса насчёт связи этих дополнительных «времён» с временем в обычном понимании.

Гипотезы многомерного времени выдвигались в физике двояко: как возможное теоретическое описание реальности или как любопытная возможность, вероятно, не имеющая отношения к известной природе. Например, Ицхак Барс опубликовал работу «Физика двухмерного времени», основанную на симметрии SO(10, 2) расширенной структуры суперсимметрии М-теории, являющийся самой современной и систематизированной разновидностью данной теории (см. также F-теория).

Если специальная теория относительности может быть обобщена на случай k-мерного времени [math]\displaystyle{ (t_1, t_2, ... , t_k) }[/math] и n-мерного пространства [math]\displaystyle{ (x_{k+1}, x_{k+2}, ... , x_{k+n}) }[/math], тогда (k + n)-размерный интервал, будучи инвариантным, даёт выражение [math]\displaystyle{ (ds_{k,n})^2 = (cdt_1)^2 + \ldots + (cdt_k)^2 -(dx_{k+1})^2 - \ldots - (dx_{k+n})^2 }[/math]. Сигнатура метрики тогда будет выглядеть следующим образом:

[math]\displaystyle{ (\underbrace{+, \cdots, +}_k, \underbrace{-, \cdots, -}_n) }[/math] — временно-подобное правило знаков,

или

[math]\displaystyle{ (\underbrace{-, \cdots, -}_k, \underbrace{+, \cdots, +}_n) }[/math] — пространственно-подобное правило знаков.

Преобразования между двумя инерциальными системами отсчёта K и K′, которые находятся в стандартной конфигурации (например, преобразование без перевода и/или вращения оси пространства в гиперплоскости пространства и/или поворотов оси времени в гиперплоскости времени) выглядят следующим образом:

[math]\displaystyle{ t'_\sigma = \sum_{\theta=1}^k \left(\delta_{\sigma\theta} t_\theta + \frac{c^2}{v_\sigma v_\theta} \beta^2(\zeta-1) t_\theta\right) - \frac{1}{v_\sigma} \beta^2 \zeta x_{k+1}, }[/math]

[math]\displaystyle{ x'_{k+1} = -c^2 \beta^2 \zeta \sum_{\theta=1}^k \frac{t_\theta}{v_\theta} + \zeta x_{k+1}, }[/math]

[math]\displaystyle{ x'_\lambda = x_\lambda, }[/math]

где [math]\displaystyle{ \mathbf{v}_1 = (v_1, \underbrace{0, \cdots, 0}_{n-1}), }[/math] [math]\displaystyle{ \mathbf{v}_2 = (v_2, \underbrace{0, \cdots, 0}_{n-1}), }[/math] [math]\displaystyle{ \mathbf{v}_k = (v_k, \underbrace{0, \cdots, 0}_{n-1}) }[/math] являются векторами скоростей K′ против K, определяют соответственно в зависимости от размеров времени t₁, t₂, …, t_k; [math]\displaystyle{ \beta = \frac{1}{\sqrt{\sum_{\mu=1}^k \frac{c^2}{v^2_\mu}}}; }[/math] [math]\displaystyle{ \zeta = \frac{1}{\sqrt{1 - \beta^2}}; }[/math] σ = 1, 2, …, k; λ = k + 2, k + 3, …, k + n. Здесь [math]\displaystyle{ \delta_{\sigma\theta} }[/math] является символом Кронекера. Эти преобразования являются обобщением преобразования Лоренца в фиксированном пространственном направлении (x_k+1) в области многомерного времени и многомерного пространства.

Причинно-следственная структура пространства-времени с двумя временными измерениями и пространством одной размерности

Обозначим: [math]\displaystyle{ \frac{dx_\eta}{dt_\sigma} = V_{\sigma\eta} }[/math], и [math]\displaystyle{ \frac{dx'_\eta}{dt'_\sigma} = V'_{\sigma\eta}, }[/math] где σ = 1, 2, …, k; η = k + 1, k + 2, …, k + n. Сложение скоростей затем даст

[math]\displaystyle{ V'_{\sigma(k+1)} = \frac{V_{\sigma(k+1)} \zeta \left(1 - \beta^2 \sum_{\theta=1}^k \frac{c^2}{v_\theta V_{\theta(k+1)}}\right)} {1 + \frac{V_{\sigma(k+1)}}{v_\sigma} \beta^2\left((\zeta - 1) \sum_{\theta=1}^k \frac{c^2}{v_\theta V_{\theta(k+1)}} - \zeta\right)}, }[/math]

[math]\displaystyle{ V'_{\sigma \lambda} = \frac{V_{\sigma \lambda}} {1 + \frac{V_{\sigma(k+1)}}{v_\sigma} \beta^2 \left((\zeta - 1) \sum_{\theta=1}^k \frac{c^2}{v_\theta V_{\theta(k+1)}} - \zeta\right)}, }[/math]

где σ = 1, 2, …, k; λ = k + 2, k + 3, …, k + n.

Для простоты рассмотрим только одну пространственную размерность x₃ и две временные размерности x₁ и x₂ (то есть, x₁ = ct₁, x₂ = ct₂, x₃ = x). Предположим, что в точке O, имеющей координаты x₁ = 0, x₂ = 0, x₃ = 0, имело место событие E. Предположим далее, что с момента события E прошёл интервал времени [math]\displaystyle{ \Delta T = \sqrt{(\Delta t_1)^2 + (\Delta t_2)^2} \geqslant 0 }[/math]. Причинно-следственная область, связанная с событием E, включает в себя боковую поверхность прямого кругового конуса {(x₁)² + (x₂)² − (x₃)² = 0}, боковую поверхность прямого кругового цилиндра {(x₁)² + (x₂)² = c²ΔT²} и внутреннюю область, ограниченную этими поверхностями, то есть причинно-следственная область включает в себя все точки (x₁, x₂, x₃), для которых условия

[math]\displaystyle{ (x_1)^2+ (x_2)^2 - (x_3)^2 = 0 \text{ и }|x_3| \leqslant c\Delta T }[/math] или

[math]\displaystyle{ (x_1)^2+ (x_2)^2 = c^2 {\Delta T}^2 \text{ и }|x_3| \leqslant c\Delta T }[/math] или

[math]\displaystyle{ (x_1)^2+ (x_2)^2 - (x_3)^2 \gt 0 \text{ и }(x_1)^2+ (x_2)^2 \lt c^2 {\Delta T}^2 }[/math]

являются выполненными.

Тем не менее, сигнатуры (1, 3) и (3, 1) физически эквивалентны, так как положительная длина вектора в пространстве Минковского для временноподобных интервалов — это условность, зависящая от договорённости о знаке метрического тензора. Так, некоторые физики как правило используют метрику с сигнатурой (+−−−), что приводит к положительной «длине» Минковского для времениподобных интервалов и энергии, в то время как пространственное расстояние будет иметь отрицательную «длину» Минковского. Релятивисты, однако, как правило придерживаются противоположной конвенции (−+++), что даёт для пространственного расстояния положительную «длину» Минковского.

Все вселенные многомерного времени можно рассматривать в качестве фридмонов.

Связь с антропным принципом

В качестве доказательства трёхмерности пространства (если не считать возможные измерения неподтвержденной теории струн) могут приводиться физические последствия предположения о том, что количество измерений отличается от трёх пространственных плюс одного временного. Этот аргумент выполнен в духе антропного принципа, и возможно, это первый случай его использования, пусть и до того, как концепция данного принципа была полностью сформулирована.

Неявное представление о том, что размерность существующей Вселенной является особенной, впервые высказал Лейбниц, который в «Рассуждении о метафизике» предположил, что «мир соответствует такой модели, которая является самой простой в гипотезе и самой богатой в явлениях».

Макс Тегмарк рассматривает гипотезы миров с размерностью времени T > 1 с точки зрения антропного принципа и приходит к выводу о невозможности существования разумной жизни в такой модели мира. В общем случае неизвестно функционирование физических законов в мире с многомерным временем. Если Т отлично от 1, поведение физических систем не может быть выведено из знания соответствующих дифференциальных уравнений в частных производных — задача Коши для волнового уравнения становится плохо определённой. Иными словами, в мире с многомерным временем невозможно точно рассчитать поведение физических систем в будущем, а любой расчёт физических законов будет иметь несколько решений — будущее такой вселенной невозможно спрогнозировать. Разумная жизнь, способная использовать технологии, в подобной вселенной не могла бы возникнуть. Единственный вариант однозначного решения для физических уравнений в мире с многомерным временем — это движение наблюдателя со скоростью света, когда время для него вообще не существует.

Более того, Тегмарк утверждает, что если T > 1, протоны и электроны были бы неустойчивы и могли бы распадаться на более массивные частицы. (Это не проблема, если частицы имеют достаточно низкую температуру.) При T > 1 субатомные частицы, распадающиеся в течение определённого периода, вели бы себя непредсказуемо, геодезическая линия не обязательно была бы максимальной для времени. Случай мира с размерностью пространства N = 1 и времени T = 3 обладает интересным свойством: скорость света является нижней границей скорости материальных тел, а вся материя состоит из тахионов.

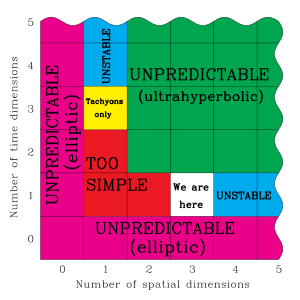
Только мир с трёхмерным пространством даёт достаточную стабильность и сложность, так как в мире с числом измерений пространства меньше 3 маловероятна гравитация и возникают топологические проблемы, а в мире с числом измерений пространства больше 3 невозможно существование стабильных орбит (для гравитационного и электромагнитного полей либо иных дальнодействующих взаимодействий). Поэтому миры с мерностью времени отличной от 1 имеют недостаток прогнозируемости, а миры с развёрнутой мерностью пространства больше 3 — недостаток стабильности. Таким образом, соблюдение антропного принципа исключает любые варианты мира помимо N = 3 и Т = 1 (или N = 1 и Т = 3 в других концепциях).

Связь с длиной Планка и скоростью света

Движение пробной частицы может быть описано координатой:

[math]\displaystyle{ x^{\mu} = \begin{pmatrix} ct \\ r\cdot f\left(\frac{\gamma\tau}{\Lambda}\right) \\ \mathbf{x} \end{pmatrix} }[/math]

которая является каноническим (1,3) вектором пространства-времени [math]\displaystyle{ (ct, \mathbf{x})^{T} }[/math] с [math]\displaystyle{ x \in \R^3 }[/math] расширенную на дополнительную временноподобную координату [math]\displaystyle{ r \cdot f (\gamma\tau /\Lambda) }[/math]. [math]\displaystyle{ \tau }[/math] тогда второй параметр времени, [math]\displaystyle{ r\in \R }[/math] описывает размер второго временного измерения и [math]\displaystyle{ \gamma }[/math] является характеристической скоростью, таким образом, эквивалент [math]\displaystyle{ c }[/math]. [math]\displaystyle{ f }[/math] описывает форму второго временного измерения и [math]\displaystyle{ \Lambda\in \R }[/math] параметр нормализации такой, что [math]\displaystyle{ \gamma\tau/\Lambda }[/math] безразмерно. Разбивая [math]\displaystyle{ x^{\mu}=x^{\mu}_t + x^{\mu}_{\tau} }[/math] с

[math]\displaystyle{ x^{\mu}_t = \begin {pmatrix} ct \\ 0 \\ \eta\mathbf{x} \end{pmatrix};\ x^{\mu}_{\tau} = \begin {pmatrix} 0 \\ r\cdot f\left(\frac{\gamma\tau}{\Lambda}\right) \\ (1-\eta)\mathbf{x} \end{pmatrix}, \eta\in(0,1) }[/math]

и используя метрику [math]\displaystyle{ (+,+,-,-,-) }[/math], тогда Лагранжева механика становится

[math]\displaystyle{ L(x,\dot{x},x^{\prime},t,\tau)=\frac{r}{\Lambda}\sqrt{\dot{c}^2t^2+c^2-\eta^2\dot{\mathbf{x}}^2+2\dot{c}ct}\sqrt{(\gamma^{\prime 2}\tau^2+\gamma^2+2\gamma \gamma^{\prime}\tau)\left(\left.\frac{df}{dz}\right|_{z=\frac{\gamma\tau}{\Lambda}}\right)^{2}-(1-\eta)^2\mathbf{x}^{\prime 2}}. }[/math]

Применение уравнения Эйлера — Лагранжа дает

[math]\displaystyle{ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_i}+\frac{d}{d\tau}\frac{\partial L}{\partial x^{\prime\ }_i}-\frac{\partial L}{\partial x_i}=0 }[/math]

Как следствие этой модели было высказано предположение, что скорость света не была постоянной в ранней Вселенной.