Линейная сепарабельность

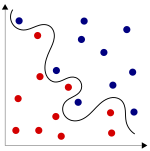
Два множества, не разделимых линейно в [math]\displaystyle{ \mathbb{R}^2 }[/math].

Два множества, разделимых линейно в [math]\displaystyle{ \mathbb{R}^2 }[/math].

Два множества точек в двумерном пространстве называются линейно сепарабельными (линейно разделимыми), если они могут быть полностью отделены единственной прямой. Для n-мерного пространства два набора точек линейно разделимы, если они могут быть отделены (n−1)-мерной гиперплоскостью.

В математических терминах: пусть [math]\displaystyle{ X_{0} }[/math] и [math]\displaystyle{ X_{1} }[/math] — два множества точек в n-мерном пространстве. Тогда [math]\displaystyle{ X_{0} }[/math] и [math]\displaystyle{ X_{1} }[/math] линейно разделимы, если существует [math]\displaystyle{ n + 1 }[/math] действительных чисел [math]\displaystyle{ w_{1}, w_{2}, ..., w_{n+1} }[/math], таких, что каждая точка [math]\displaystyle{ x \in X_{0} }[/math] удовлетворяет [math]\displaystyle{ \sum^{n}_{i=1} w_{i}x_{i}\ge w_{n+1} }[/math] и каждая точка [math]\displaystyle{ x \in X_{1} }[/math] удовлетворяет [math]\displaystyle{ \sum^{n}_{i=1} w_{i}x_{i} \lt w_{n+1} }[/math], где [math]\displaystyle{ x_{i} }[/math] — i-й компонент [math]\displaystyle{ x }[/math].

Число линейно разделимых булевых гиперкубов (функций) в зависимости от размерности пространства последовательность A000609 в OEIS

Размерность	Число линейно разделимых булевых гиперкубов
2	14
3	104
4	1882
5	94572
6	15028134
7	8378070864
8	17561539552946
9	144130531453121108

См. также

• Сепарабельность
• Перцептрон - устройство и алгоритм, который позволяет линейно разделить любые нелинейные множества в пространстве
• Линейный классификатор