Каон

Као́н (или K-мезо́н^[1], обозначается K) — мезон, содержащий один странный антикварк и один u- или d-кварк (антикаоны, напротив, содержат один странный кварк и один u- или d-антикварк). Каоны — самые лёгкие из всех странных (то есть имеющих ненулевое квантовое число, называемое странностью) адронов.

Основные свойства

Существуют четыре каона с определённой массой:

Отрицательно заряженный K⁻ (содержащий s-кварк и u-антикварк) имеет массу 493,667(16) МэВ и время жизни 1,2380(21)⋅10⁻⁸ секунд.
Его античастица, положительно заряженный K⁺ (содержащий u-кварк и s-антикварк) согласно CPT-симметрии должен иметь массу и время жизни, равные соответственно массе и времени жизни K⁻. Экспериментально измеренная разность масс составляет 0,032(90) МэВ, то есть совместима с нулём. Разность во времени жизни также нулевая (экспериментальный результат: Δτ = 0,11(9)⋅10⁻⁸ секунды).
K⁰ (содержащий d-кварк и s-антикварк) имеет массу 497,614(24) МэВ.
Его античастица [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math] (содержащая s-кварк и d-антикварк) имеет такую же массу.

Из кварковой модели ясно, что каоны формируют два изоспиновых дублета; то есть они принадлежат к фундаментальному представлению группы SU(2), называемому 2. Один дублет со странностью +1 и изоспином +1/2 содержит K⁺ и K⁰. Античастицы формируют второй дублет со странностью −1 и изоспином −1/2.

Частица	Символ	Анти- частица	Кварковый состав частицы	Спин и чётность, [math]\displaystyle{ J^{\pi} }[/math]	Масса МэВ/c²	S	Время жизни с	Распадается на	Примечания
Заряженный каон	[math]\displaystyle{ \mathrm{K^+} }[/math]	[math]\displaystyle{ \mathrm{K^-} }[/math]	[math]\displaystyle{ \mathrm{u\bar{s}} }[/math]	Псевдоскаляр (0⁻)	493,667(16)	+1	1,24⋅10⁻⁸	μ+ν_μ или π⁺+π₀ или π⁺+π⁺+π⁻ или π⁰+e⁺+ν_e
Нейтральный каон	[math]\displaystyle{ \mathrm{K^0} }[/math]	[math]\displaystyle{ \mathrm{\bar{K}^0} }[/math]	[math]\displaystyle{ \mathrm{d\bar{s}} }[/math]	Псевдоскаляр (0⁻)	497,614(24)	+1	слабый распад см. ниже		Сильное собственное состояние — нет определённого времени жизни
Короткоживущий каон	[math]\displaystyle{ \mathrm{K_S^0} }[/math]	[math]\displaystyle{ \mathrm{K_S^0} }[/math]	[math]\displaystyle{ \mathrm{\frac{d\bar{s} + s\bar{d}}{\sqrt{2}}} }[/math]	Псевдоскаляр (0⁻)	497,614(24)	(*)	0,89⋅10⁻¹⁰	π⁺ + π⁻ или 2π⁰	Слабое собственное состояние — состав указывает на нарушение CP-инвариантности
Долгоживущий каон	[math]\displaystyle{ \mathrm{K_L^0} }[/math]	[math]\displaystyle{ \mathrm{K_L^0} }[/math]	[math]\displaystyle{ \mathrm{\frac{d\bar{s} - s\bar{d}}{\sqrt{2}}} }[/math]	Псевдоскаляр (0⁻)	497,614(24)	(*)	5,2⋅10⁻⁸	π^±+e^∓+ν_e или π^±+μ^∓+ν_μ или 3π⁰ или π⁺+π⁰+π⁻	Слабое собственное состояние — состав указывает на нарушение CP-инвариантности

Хотя K⁰ и его античастица [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math] обычно появляются в результате сильного взаимодействия, они распадаются посредством слабого взаимодействия. Следовательно, их можно рассматривать как композицию двух слабых собственных состояний, которые имеют очень различные времена жизни:

Долгоживущий нейтральный каон, обозначаемый K_L («K-long»), обычно распадается на три пиона и имеет время жизни 5,18⋅10⁻⁸ секунд.
Короткоживущий нейтральный каон, обозначаемый K_S («K-short»), обычно распадается на два пиона и имеет время жизни 8,958⋅10⁻¹¹ секунд.

(См. обсуждение смешивания нейтральных каонов ниже.)

Эксперименты 1964 г., показавшие, что K_L редко распадается на два пиона, привели к открытию нарушения CP-инвариантности (см. ниже).

Основные варианты распада для K⁺:

[math]\displaystyle{ \mu^+\nu_\mu }[/math] (лептонный, коэффициент ветвления BR = 63,55(11)%);
[math]\displaystyle{ \pi^+\pi^0 }[/math] (адронный, BR = 20,66(8)%);
[math]\displaystyle{ \pi^+\pi^+\pi^- }[/math] (адронный, BR = 5,59(4)%);
[math]\displaystyle{ \pi^0e^+\nu_e }[/math] (полулептонный, BR = 5,07(4)%);
[math]\displaystyle{ \pi^0\mu^+\nu_{\mu} }[/math] (полулептонный, BR = 3,353(34)%);
[math]\displaystyle{ \pi^+\pi^0\pi^0 }[/math] (адронный, BR = 1,761(22)%).

Странность

Открытие адронов со внутренним квантовым числом — «странностью» — положило начало самой поразительной эпохе в физике элементарных частиц, которая даже сейчас, пятьдесят лет спустя, не дошла до своего завершения… Именно большие эксперименты определили это развитие, и основные открытия появлялись неожиданно или даже вопреки ожиданиям теоретиков.
— Bigi I. I., Sanda A.I. CP Violation (англ.). — New York: Cambridge Univ. Press, 2000. — 382 p. — ISBN 0-521-44349-0.

В 1947 г. Дж. Рочестер и К. К. Батлер опубликовали две фотографии событий в камере Вильсона, вызванных космическими лучами; на одной была показана нейтральная частица, распадающаяся на два заряженных пиона, а на другой — заряженная частица, распадающаяся на заряженный пион и что-то нейтральное. Оценка масс новых частиц была грубой — приблизительно половина массы протона. Дальнейшие примеры этих «V-частиц» появились не скоро.

Первый прорыв был совершён в Калтехе, где камера Вильсона была доставлена на гору Вильсона для более эффективного наблюдения за космическими лучами. В 1950 г. было замечено 30 заряженных и 4 нейтральных V-частицы. Вдохновлённые этим, учёные проводили множество наблюдений на вершине горы несколько последующих лет, и к 1953 г. была принята следующая классификация: «L-мезон» означало мюон или пион. «K-мезон» означало частицу, имевшую массу между массами пиона и нуклона. «Гиперон» означало любую частицу тяжелее нуклона.

Распады были очень медленными; типичные времена жизни были порядка 10⁻¹⁰ секунды. Однако рождение частиц в пион-протонных реакциях происходило намного быстрее, с характерным временем порядка 10⁻²³ секунды. Проблема этого несоответствия была решена Абрахамом Пайсом, постулировавшим существование нового квантового числа, названного «странностью», которое сохраняется при сильном взаимодействии, но не сохраняется при слабом. Странные частицы появлялись в больших количествах из-за «связанного рождения» одновременно странной и антистранной частицы. Вскоре было показано, что оно не является мультипликативным квантовым числом, поскольку иначе были бы разрешены реакции, которые не наблюдались на новых циклотронах, построенных в Брукхейвенской Национальной лаборатории в 1953 г. и в Национальной лаборатории Лоуренса в Беркли в 1955 г.

Нарушение чётности: загадка θ-τ

Для заряженных странных мезонов было найдено два типа распада:

θ⁺ → π⁺ + π⁰
τ⁺ → π⁺ + π⁺ + π⁻.

Поскольку два конечных состояния имеют разную чётность, предполагалось, что начальные состояния также должны иметь разную чётность, и следовательно быть двумя разными частицами. Однако более точные измерения не показали никакой разницы в их массах и временах жизни, доказав, что они являются одной и той же частицей. Это явление известно как загадка θ-τ. Она была решена только с открытием нарушения чётности в слабых взаимодействиях. Поскольку мезоны распадаются посредством слабого взаимодействия, чётность не должна сохраняться, и два распада могут быть вызваны одной частицей, сейчас называемой K⁺.

Нарушение CP-симметрии в осцилляциях нейтральных мезонов

Сначала считалось, что, хотя чётность нарушается, CP (заряд+чётность) симметрия сохраняется. Чтобы понять открытие нарушения CP-симметрии, необходимо понять смешивание нейтральных каонов; это явление не требует нарушения CP-симметрии, но именно в этом контексте впервые наблюдалось нарушение CP-симметрии.

Смешивание нейтральных каонов

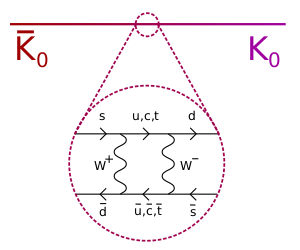
Два разных нейтральных K мезона, имеющих разную странность, могут превращаться друг в друга посредством слабого взаимодействия, поскольку в этом взаимодействии не сохраняется странность. s-Кварк в K⁰ превращается в d-кварк, испуская два W-бозона противоположных зарядов. d-Антикварк в K⁰ превращается в s-антикварк, поглощая их.

Поскольку нейтральные каоны имеют странность, они не могут быть своими собственными античастицами. Тогда должно быть два разных нейтральных каона, различающихся на две единицы странности. Вопрос в том, как установить существование этих двух мезонов. Решение использует явление, названное осцилляции нейтральных частиц, при котором эти два вида мезонов могут превращаться друг в друга посредством слабого взаимодействия, которое заставляет их распадаться на пионы (см. прилагаемый рисунок).

Эти осцилляции впервые были исследованы Мюрреем Гелл-Манном и Абрахамом Пайсом в их совместной работе. Они рассмотрели CP-инвариантную временную эволюцию состояний с противоположной странностью. В матричных обозначениях можно написать

[math]\displaystyle{ \psi(t) = U(t)\psi(0) = {\rm e}^{iHt} \begin{pmatrix}a \\ b\end{pmatrix}, \qquad H =\begin{pmatrix}M & \Delta\\ \Delta & M\end{pmatrix} }[/math]

где ψ — это квантовое состояние системы, характеризуемое амплитудами существования в каждом из двух основных состояний (которые обозначены a и b во время t = 0). Диагональные элементы (M) гамильтониана соответствуют сильному взаимодействию, при котором сохраняется странность. Два диагональных элемента должны быть равными, поскольку частица и античастица имеют равные массы в отсутствие слабого взаимодействия. Не лежащие на диагонали элементы, которые смешивают частицы с противоположной странностью, вызваны слабым взаимодействием; CP-симметрия требует, чтобы они были действительными.

Если матрица H действительна, вероятности двух состояний будут вечно колебаться взад и вперёд. Однако, если какая-то часть матрицы будет мнимой, хотя это запрещено CP-инвариантностью, тогда часть комбинации со временем будет уменьшаться. Уменьшающейся частью может быть либо одна компонента (a), либо другая (b), либо смесь обеих.

Смешивание

Собственные состояния получаются при диагонализации этой матрицы. Это даёт новые собственные векторы, которые мы можем назвать K₁, который является суммой двух состояний с противоположной странностью, и K₂, который является разностью. Оба они являются собственными состояниями CP с противоположными собственными значениями; K₁ имеет CP = +1, а K₂ имеет CP = −1. Поскольку двухпионное конечное состояние также имеет CP = +1, только K₁ может распадаться этим путём. K₂ должен распадаться на три пиона. Поскольку масса K₂ немного больше суммы масс трёх пионов, этот распад происходит очень медленно, примерно в 600 раз медленнее, чем распад K₁ на два пиона. Эти два пути распада наблюдались Леоном Ледерманом и его коллегами в 1956 г., которые установили существование двух слабых собственных состояний (состояний с определённым временем жизни при распаде нейтральных каонов посредством слабого взаимодействия) нейтральных каонов.

Эти два собственных состояния были названы K_L (K-long) и K_S (K-short). CP-симметрия, которая в то время считалась незыблемой, предполагает, что K_S = K₁ и K_L = K₂.

Осцилляция

Изначально чистый пучок K⁰ будет при распространении превращаться в свои античастицы, которые затем будут превращаться обратно в начальные частицы, и так далее. Это явление было названо осцилляцией частиц. При наблюдениях распадов на лептоны выяснилось, что K⁰ всегда распадался с эмиссией электрона, в то время как античастица [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math] — с эмиссией позитрона. При первом анализе было выявлено соотношение между уровнем рождения электронов и позитронов из источников чистых K⁰ и их античастиц [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math]. Анализ зависимости по времени полулептонного распада доказал существование явления осцилляций и позволил выяснить расщепление масс между K_S и K_L. Поскольку оно существует благодаря слабому взаимодействию, оно очень мало, 3,483(6)⋅10⁻¹² МэВ (10⁻¹⁵ массы каждого состояния).

Восстановление

Пучок нейтральных каонов в полёте распадается так, что короткоживущий K_S исчезает, оставляя поток чистых долгоживущих K_L. Если этот поток проходит через вещество, K⁰ и его античастица [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math] по-разному взаимодействуют с ядрами. С K⁰ происходит квазиупругое рассеяние на нуклонах, в то время как его античастица может создавать гипероны. Из-за различного взаимодействия двух компонент теряется квантовая когерентность между двумя частицами. Возникающий поток содержит различные линейные суперпозиции K⁰ и [math]\displaystyle{ \mathrm{\bar{K}^0} }[/math]. Такая суперпозиция является смесью K_L и K_S; таким образом, K_S восстанавливается при прохождении пучка нейтральных каонов через вещество. Восстановление наблюдалось Оресте Пиччони и его коллегами в Национальной лаборатории Лоуренса в Беркли. Вскоре после этого, Роберт Адэр со своими помощниками сообщил об избыточном восстановлении K_S, тем самым открыв новую главу в этой истории.

Нарушение CP-симметрии

Пытаясь проверить результаты Адэра, в 1964 г. Джеймс Кронин и Вэл Фитч из BNL обнаружили распад K_L на два пиона (CP = +1). Как указано выше, этот распад требует, чтобы предполагаемые начальные и конечные состояния имели различные значения CP, и, следовательно, немедленно предполагает нарушение CP-симметрии. Другие объяснения, такие как нелинейность квантовой механики или новая элементарная частица (гиперфотон), вскоре были отброшены, оставив нарушение CP-симметрии единственной возможностью. За это открытие Кронин и Фитч получили Нобелевскую премию по физике 1980 г.

Выяснилось, что хотя K_L и K_S являются слабыми собственными состояниями (потому что они имеют определённое время жизни при распаде посредством слабого взаимодействия), они не совсем CP-состояния. Вместо этого, с точностью до нормировочного множителя

K_L = K₂ + εK₁

(и аналогично для K_S), где ε — малый параметр. Таким образом, изредка K_L распадается как K₁ с CP = +1, и аналогично K_S может распадаться как K₂ с CP = −1. Это явление известно как непрямое нарушение CP-симметрии, нарушение CP-симметрии из-за смешивания K⁰ и его античастицы. Существует также и прямое нарушение CP-симметрии, при котором нарушение происходит при самом распаде. Оба эффекта наблюдаются, поскольку и смешивание, и распад происходят от одного и того же взаимодействия с W-бозоном и, таким образом, нарушение CP-симметрии предсказывается ККМ-матрицей.

См. также

Примечания

↑ КАОНЫ • Большая Российская Энциклопедия (неопр.). Дата обращения: 4 июня 2016. Архивировано 23 апреля 2016 года.

Ссылки

Particle data group (2010) on mesons
The quark model, by J.J.J. Kokkedee
CP violation, by I.I. Bigi and A.I. Sanda (Cambridge University Press, 2000) ISBN 0-521-44349-0
Griffiths, David (1987). Introduction to Elementary Particles. New York: John Wiley & Sons. ISBN 0-471-60386-4.
В. М. Терентьев. Распад [math]\displaystyle{ K_2 \rightarrow 2\pi }[/math] и возможное несохранение CP-чётности. — УФН, т.86, 1965, вып. 2, с. 231—262.
Cirigliano V. et al. Kaon decays in the standard model (англ.) // Rev. Mod. Phys.. — 2012. — Vol. 84. — P. 399—447. — doi:10.1103/RevModPhys.84.399.

[1] КАОНЫ • Большая Российская Энциклопедия (неопр.). Дата обращения: 4 июня 2016. Архивировано 23 апреля 2016 года.

[1]