Перейти к содержанию

Изохорный процесс

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «Изохорический процесс»)
Статья является частью одноименной серии.
Тепловые процессы
См. также «Физический портал»

Изохо́рный, или изохори́ческий проце́сс (от др.-греч. ἴσος — «равный» и χώρος — «место») — термодинамический изопроцесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать или охлаждать вещество в сосуде неизменного объёма.

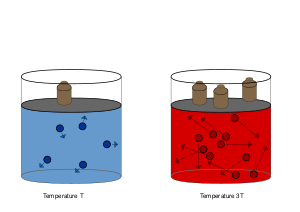
При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля выполняется приближённо.

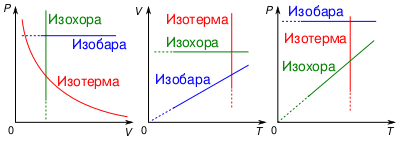
На графиках в координатах состояния ([math]\displaystyle{ P-V,\ P-T,\ V-T }[/math]) изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: [math]\displaystyle{ T }[/math] (температура), [math]\displaystyle{ V }[/math] (объем) и [math]\displaystyle{ P }[/math] (давление).

История

Иллюстрация зависимости давления от температуры при постоянном объёме

Наиболее часто первые исследования изохорного процесса связывают с Гийомом Амонтоном. В своей работе «Парижские мемуары» в 1702 году он описал поведение газа в фиксированном объёме[Комм 1] внутри так называемого «воздушного термометра». Жидкость в нём находится в равновесии под воздействием давления газа в резервуаре и атмосферным давлением. При нагревании давление в резервуаре увеличивается, и жидкость вытесняется в выступающую трубку. Зависимость между температурой и давлением была установлена в виде[1][Комм 2]:

[math]\displaystyle{ \frac{p_1}{p_2}=\frac{1+\alpha t_1}{1+\alpha t_2}. }[/math]

В 1801 году Джон Дальтон в двух своих эссе опубликовал эксперимент, в котором установил, что все газы и пары, исследованные им при постоянном давлении, одинаково расширяются при изменении температуры, если начальная и конечная температура одинакова[2][3][4]. Данный закон получил название закона Гей-Люссака, так как Гей-Люссак вскоре провёл самостоятельные эксперименты и подтвердил одинаковое расширение различных газов, причём получив практически тот же самый коэффициент, что и Дальтон[4]. Впоследствии он же объединил свой закон с законом Бойля — Мариотта[5], что позволило описывать в том числе и изохорный процесс.

Термодинамика процесса

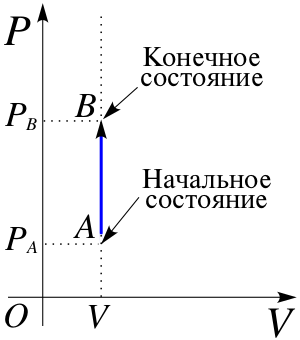
График изохорного процесса на диаграмме в координатах [math]\displaystyle{ P,\ V }[/math]
Графики изопроцессов в идеальном газе

Из определения работы следует, что элементарная работа при термодинамическом процессе равна[6][Комм 3]:

[math]\displaystyle{ \delta A = P dV. }[/math]

Чтобы определить полную работу процесса проинтегрируем данное выражение[6]:

[math]\displaystyle{ A = \int\limits_{V_1}^{V_1}PdV, }[/math]

но, поскольку объём неизменен, то есть [math]\displaystyle{ \Delta V = 0 }[/math], то такой интеграл равен нулю. Поэтому при изохорном процессе газ работы не совершает[7]:

[math]\displaystyle{ A=0. }[/math]

Это же можно показать на графике изохорного процесса. С математической точки зрения, работа процесса равна площади такого графика[6]. Но график изохорного процесса является прямой перпендикулярной к оси объёма. Таким образом, площадь под ним равна нулю.

Изменение внутренней энергии идеального газа можно найти по формуле[8]:

[math]\displaystyle{ \Delta U=\frac{i}{2}\nu R\Delta T, }[/math]
где [math]\displaystyle{ i }[/math] — число степеней свободы, которое зависит от количества атомов в молекуле газа (3 — для одноатомной (например, неон), 5 — для двухатомной (например, кислород) и 6 — для трёхатомной и более (например, молекула углекислого газа)).

Из определения и формулы теплоёмкости формулу для внутренней энергии можно переписать в виде[8]:

[math]\displaystyle{ \Delta U=\nu\ c_v^{\mu}\ \Delta T, }[/math]
где [math]\displaystyle{ c_v^{\mu} }[/math] — молярная теплоёмкость при постоянном объёме.

Используя первое начало термодинамики можно найти количество теплоты при термодинамическом процессе[9]:

[math]\displaystyle{ Q =\Delta U + A. }[/math]

Но при изохорном процессе газ не выполняет работу[7]. То есть, имеет место равенство:

[math]\displaystyle{ Q = \Delta U = \nu\ c_v^{\mu}\ \Delta T, }[/math]

таким образом, вся теплота, которую получает газ, идёт на изменение его внутренней энергии.

Энтропия при изохорном процессе

Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует[10]:

[math]\displaystyle{ dS = {\delta Q \over T}, }[/math]
где [math]\displaystyle{ \delta Q }[/math] — элементарное количество теплоты[11][Комм 3].

Выше была выведена формула для определения количества теплоты. Если её переписать в дифференциальном виде[12][Комм 4]:

[math]\displaystyle{ \delta Q = \nu\ c_v^{\mu}\ dT, }[/math]
где [math]\displaystyle{ \nu }[/math] — количество вещества,
[math]\displaystyle{ c_v^\mu }[/math] — молярная теплоемкость при постоянном объёме.

Микроскопическое изменение энтропии при изохорном процессе можно определить по формуле[12]:

[math]\displaystyle{ dS = {\nu\ c_v^{\mu}\ dT \over T}dy/dx\ dy/dx. }[/math]

Или, если проинтегрировать последнее выражение, полное изменение энтропии в этом процессе[12]:

[math]\displaystyle{ \int\limits_{S_1}^{S_2} dS = \nu \int\limits_{T_1}^{T_2}{c_v^{\mu}\ dT \over T} \Rightarrow \Delta S=\nu\int\limits_{T_1}^{T_2}{c_v^{\mu}\ dT \over T}. }[/math]

В данном случае выносить выражение молярной теплоемкости при постоянном объёме за знак интеграла нельзя, поскольку она является функцией, которая зависит от температуры.

Практическое применение теории изохорного процесса

[math]\displaystyle{ p-V }[/math] диаграмма цикла Отто
Основные статьи: Цикл Отто, Цикл Стирлинга и Адиабатический процесс

При идеальном цикле Отто, который приближённо воспроизведён в бензиновом двигателе внутреннего сгорания, такты 2—3 и 4—1 являются изохорными процессами.

Работа, совершаемая на выходе двигателя, равна разности работ, которую произведёт газ над поршнем во время третьего такта (то есть рабочего хода), и работы, которую затрачивает поршень на сжатие газа во время второго такта. Так как в двигателе, работающем по циклу Отто используется система принудительного зажигания смеси, то происходит сжатие газа в 7—12 раз[13].

Анимация классического двигателя Стирлинга с конфигурацией бета-типа, при которой рабочий и вытеснительный поршни скомпонованы в одном цилиндре

В цикле Стирлинга также присутствуют два изохорных такта. Для его осуществления в двигателе Стирлинга добавлен регенератор. Газ, проходя через наполнитель в одну сторону, отдаёт тепло от рабочего тела к регенератору, а при движении в другую сторону отдаёт его обратно рабочему тему[14]. Идеальный цикл Стирлинга достигает обратимости и тех же величин КПД что и цикл Карно[15].

См. также

Примечания

Комментарии

  1. ↑ В приведённом опыте изменения объёма пренебрежимо малы по сравнению с изменением давления
  2. ↑ При эксперименте использовалась шкала температур в градусах Цельсия, а не Кельвина
  3. ↑ Перейти обратно: 3,0 3,1 . Также используются обозначения [math]\displaystyle{ d^\prime Q }[/math] и [math]\displaystyle{ d^\prime A }[/math]
  4. ↑ В источнике даны формулы для всех термодинамических процессов. В частности, данная формула в полном виде имеет значение [math]\displaystyle{ \delta Q = \nu\ c_v^{\mu}\ dT \, + PdV }[/math], но при изохорном процессе [math]\displaystyle{ dV=0 }[/math]

Источники

  1. ↑ Кудрявцев, 1956, с. 292—293.
  2. ↑ J. Dalton, 1802, с. 550—574.
  3. ↑ J. Dalton, 1802, с. 595—602.
  4. ↑ Перейти обратно: 4,0 4,1 Кудрявцев, 1956, с. 393.
  5. ↑ Кудрявцев, 1956, с. 396.
  6. ↑ Перейти обратно: 6,0 6,1 6,2 Савельев, 2001, с. 19—21.
  7. ↑ Перейти обратно: 7,0 7,1 Савельев, 2001, с. 37.
  8. ↑ Перейти обратно: 8,0 8,1 Савельев, 2001, с. 61.
  9. ↑ Савельев, 2001, с. 17.
  10. ↑ Савельев, 2001, с. 93.
  11. ↑ Савельев, 2001, с. 18.
  12. ↑ Перейти обратно: 12,0 12,1 12,2 Сивухин, 1975, с. 128.
  13. ↑ Кириллин, 2008.
  14. ↑ Romanelli, 2017.
  15. ↑ Крестовников А. Н., Вигдорович В. Н., Химическая термодинамика, 1973, с. 63.

Список литературы

  1. Кириллин В. А., Сычёв В. В., Шейндлин А. Е. Техническая термодинамика: учебник для вузов. — М.: Издательство МЭИ, 2008. — 496 с. Архивная копия от 24 ноября 2011 на Wayback Machine
  2. Крестовников А. Н., Вигдорович В. Н. Химическая термодинамика. — 2-е изд., испр. и доп. — М.: Металлургия, 1973. — 256 с.
  3. Кудрявцев П. С. История физики. — М.: Гос. учебно-педагог. изд-во, 1956. — Т. 1. От античной физики до Менделеева. — 564 с. — 25 000 экз.
  4. Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2005. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
  5. Савельев И. В. Курс общей физики:Молекулярная физика и термодинамика. — М.: Астрель, 2001. — Т. 3. — 208 с. — 7000 экз. — ISBN 5-17-004585-9.
  6. Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.
  7. J. Dalton. 2 // Memoirs of the Literary and Philosophical Society of Manchester. — 1802. — Т. 5. — 701 с.
  8. Alejandro Romanelli. Alternative thermodynamic cycle for the Stirling machine. — Montevideo, Uruguay: Instituto de F´ısica, Facultad de Ingenier´ıa Universidad de la Rep´ublica, 2017.


Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Изохорный_процесс&oldid=7035997