Изотомическое сопряжение
В планиметрии изотоми́ческим сопряже́нием называется одно из преобразований плоскости, порождаемое заданным на плоскости треугольником ABC.
Определение
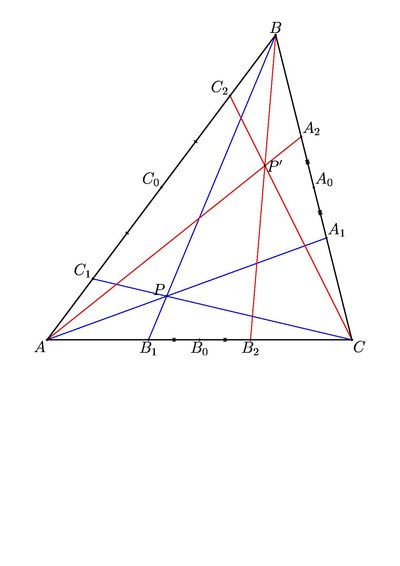
Пусть дан треугольник [math]\displaystyle{ ABC }[/math], у которого [math]\displaystyle{ A_0 }[/math] — середина стороны [math]\displaystyle{ BC }[/math], [math]\displaystyle{ B_0 }[/math] — середина [math]\displaystyle{ AC }[/math] и [math]\displaystyle{ C_0 }[/math] — середина стороны [math]\displaystyle{ AB }[/math]. Пусть также на плоскости выбрана произвольная точка [math]\displaystyle{ P }[/math], не лежащая на прямых, содержащих его стороны. Тогда рассмотрим прямые [math]\displaystyle{ AP }[/math], [math]\displaystyle{ BP }[/math] и [math]\displaystyle{ CP }[/math]. Пусть они пересекают прямые, содержащие противолежащие стороны треугольника, соответственно в точках [math]\displaystyle{ A_1 }[/math], [math]\displaystyle{ B_1 }[/math] и [math]\displaystyle{ C_1 }[/math] (если прямые окажутся параллельными, точкой пересечения считается бесконечно удалённая точка прямой). Согласно теореме Чевы, [math]\displaystyle{ \frac{AC_1}{C_1B}\cdot\frac{BA_1}{A_1C}\cdot\frac{CB_1}{B_1A}=1 }[/math]. Если теперь точки [math]\displaystyle{ A_1 }[/math], [math]\displaystyle{ B_1 }[/math] и [math]\displaystyle{ C_1 }[/math] симметрично отразить относительно [math]\displaystyle{ A_0 }[/math], [math]\displaystyle{ B_0 }[/math] и [math]\displaystyle{ C_0 }[/math] соответственно, получатся точки [math]\displaystyle{ A_2 }[/math], [math]\displaystyle{ B_2 }[/math] и [math]\displaystyle{ C_2 }[/math] (бесконечно удалённая точка переходит сама в себя). Поскольку [math]\displaystyle{ AC_1=BC_2 }[/math], [math]\displaystyle{ AC_2=BC_1 }[/math] и так же для остальных пар точек, получаем [math]\displaystyle{ 1=\frac{AC_1}{C_1B}\cdot\frac{BA_1}{A_1C}\cdot\frac{CB_1}{B_1A}=\frac{BC_2}{C_2A}\cdot\frac{CA_2}{A_2B}\cdot\frac{AB_2}{B_2C} }[/math] и, согласно той же теореме Чевы, прямые [math]\displaystyle{ AA_2 }[/math], [math]\displaystyle{ BB_2 }[/math] и [math]\displaystyle{ CC_2 }[/math] пересекаются в одной точке [math]\displaystyle{ P' }[/math]. Эта точка называется изотомически сопряжённой точке [math]\displaystyle{ P }[/math] относительно треугольника [math]\displaystyle{ ABC }[/math].
Изотомическое сопряжение устанавливает взаимно-однозначное соответствие между точками плоскости с исключёнными прямыми [math]\displaystyle{ AB }[/math], [math]\displaystyle{ BC }[/math] и [math]\displaystyle{ AC }[/math]. На этих прямых соответствие не является взаимно-однозначным, так любой точке прямой [math]\displaystyle{ BC }[/math] соответствует вершина [math]\displaystyle{ A }[/math] (и наоборот, вершине [math]\displaystyle{ A }[/math] — всякая точка [math]\displaystyle{ BC }[/math]) и так далее.
Координаты
Если барицентрические координаты точки [math]\displaystyle{ P }[/math] суть [math]\displaystyle{ (p:q:r) }[/math], то барицентрические координаты изотомически сопряжённой ей точки [math]\displaystyle{ P' }[/math] суть [math]\displaystyle{ \left(\frac1{p}:\frac1{q}:\frac1{r}\right) }[/math].
Если трилинейные координаты точки [math]\displaystyle{ P }[/math] суть [math]\displaystyle{ (p:q:r) }[/math], то трилинейные координаты изотомически сопряжённой ей точки [math]\displaystyle{ P' }[/math] суть [math]\displaystyle{ \left(\frac1{a^2p}:\frac1{b^2q}:\frac1{c^2r}\right) }[/math].
Другое определение
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Свойства
- Изотомическое сопряжение является инволюцией, то есть его квадрат тривиален.
- Неподвижными точками (то есть переходящими сами в себя) изотомического сопряжения являются центроид (другие названия: барицентр или центр масс, то есть точка пересечения медиан) треугольника [math]\displaystyle{ ABC }[/math] и точки, симметричные вершинам треугольника относительно середин противолежащих сторон.
- Точки Жергонна и Нагеля изотомически сопряжены.
- Точке Лемуана (точке пересечения симедиан) треугольника изотомически сопряжена его точка Брокара.
- Точке пересечения биссектрис (инцентру) изотомически сопряжена точка пересечения антибиссектрис,
- Прямые общего положения относительно треугольника при изотомическом сопряжении переходят в описанные вокруг него коники, и наоборот.