Генерация второй оптической гармоники

Генерация второй гармоники (ГВГ) — нелинейно-оптический процесс, в котором фотоны с одинаковой частотой, взаимодействуя с нелинейным материалом, объединяются для формирования новых фотонов с удвоенной энергией, и, следовательно, с удвоенной частотой и длиной волны в половину меньшей начальной. Это частный случай нелинейного сложения частот излучения.

Объяснение эффекта можно также найти в Видео на YouTube.

История

Генерация второй гармоники была впервые реализована Питером Франкеном, Хиллом, Петерсом и Вайнрайхом в Университете Мичигана, Анн-Арборе, в 1961 году.^[1] Реализация стала возможной благодаря изобретению лазера, который создал необходимую высокую интенсивность монохроматического излучения. В этом опыте излучение, генерируемое рубиновым лазером, фокусировалось в кристалл кварца. Выходное излучение разворачивали в спектр при помощи дисперсионной призмы и фокусировали на фотопластинку. В результате можно было наблюдать, что помимо света на частоте лазера из кристалла выходило излучение на длине волны 347 нм. Это и была вторая гармоника. Позже эксперименты по ГВГ повторили Джордмейн^[2], Мейкер и др^[3]., Миллер и Сейвидж и др^[4].

Вывод уравнения

Уравнение для частотной компоненты поля с частотой [math]\displaystyle{ \omega_n }[/math] может быть записано как^[5]

[math]\displaystyle{ \nabla^{2} \mathbf{E}_{n}(\mathbf{r})+\frac{\omega_{n}^{2}}{c^{2}} {\varepsilon}\left(\omega_{n}\right) \cdot \mathbf{E}_{n}(\mathbf{r})=-\frac{\omega_{n}^{2}}{\varepsilon_{0} c^{2}} \mathbf{P}_{n}^{\mathrm{NL}}(\mathbf{r}) }[/math]

где [math]\displaystyle{ \varepsilon\left(\omega_{n}\right) }[/math] — диэлектрическая проницаемость материала на частоте [math]\displaystyle{ \omega_n }[/math].

Рассмотрим общий случай генерации суммарной частоты [math]\displaystyle{ \omega_3 }[/math] двумя волнами с частотами [math]\displaystyle{ \omega_1 }[/math] и [math]\displaystyle{ \omega_2 }[/math]. Генерация второй гармоники — частный случай при [math]\displaystyle{ \omega_1=\omega_2=\omega }[/math], [math]\displaystyle{ \omega_3=\omega_1+\omega_2=2\omega }[/math]. Будем считать, что волна распространяется в направлении z, и векторные величины можно заменить скалярными.

Тогда поляризованность

[math]\displaystyle{ P_3(\omega_3) = \varepsilon_0 \chi^{(2)} E_1(\omega_1)E_2(\omega_2) = 4\varepsilon_0 d_\text{eff}(\omega_3; \omega_1, \omega_2) E_1(\omega_1)E_2(\omega_2),\, }[/math]

(в случае второй гармоники [math]\displaystyle{ P(2\omega) = \varepsilon_0 \chi^{(2)} E^2(\omega) = 2\varepsilon_0 d_\text{eff}(2\omega; \omega, \omega) E^2(\omega) }[/math])

где [math]\displaystyle{ d_\text{eff} }[/math] — эффективный нелинейно-оптический коэффициент.

Учтем, что

[math]\displaystyle{ E_i(z,t)=E_i(\omega_i)e^{-i\omega_it} }[/math]

[math]\displaystyle{ E_i(\omega_i)=A_ie^{ik_iz} }[/math]

тогда

[math]\displaystyle{ P_3(\omega_3) = 4\varepsilon_0 d_\text{eff} A_1A_2e^{ik_1z+ik_2z},\, }[/math]

При подстановке в волновое уравнение получаем

[math]\displaystyle{ \begin{array}{c} {\left[\frac{d^{2} A_{3}}{d z^{2}}+2 i k_{3} \frac{d A_{3}}{d z}-k_{3}^{2} A_{3}+\frac{\varepsilon\left(\omega_{3}\right) \omega_{3}^{2} A_{3}}{c^{2}}\right] e^{i\left(k_{3} z-\omega_{3} t\right)}+\mathrm{c.c.}} =\frac{-4 d_{\mathrm{eff}} \omega_{3}^{2}}{c^{2}} A_{1} A_{2} e^{i\left[\left(k_{1}+k_{2}\right) z-\omega_{3} t\right]}+\mathrm{c.c.} \end{array} }[/math]

поскольку [math]\displaystyle{ k_3^2=\varepsilon\left(\omega_{3}\right)\omega_{3}^{2} A_{3}/c^{2} }[/math], получаем

[math]\displaystyle{ \frac{d^{2} A_{3}}{d z^{2}}+2 i k_{3} \frac{d A_{3}}{d z}=\frac{-4 d_{\mathrm{eff}} \omega_{3}^{2}}{c^{2}} A_{1} A_{2} e^{i\left(k_{1}+k_{2}-k_{3}\right) z} }[/math]

Воспользуемся приближением медленно меняющихся амплитуд:

[math]\displaystyle{ \frac{d A_{3}}{d z}=\frac{2 i d_{\mathrm{eff}} \omega_{3}^{2}}{k_{3} c^{2}} A_{1} A_{2} e^{i \Delta k z} }[/math]

[math]\displaystyle{ \begin{aligned} \frac{d A_{1}}{d z} &=\frac{2 i d_{\mathrm{eff}} \omega_{1}^{2}}{k_{1} c^{2}} A_{3} A_{2}^{*} e^{-i \Delta k z} \\ \frac{d A_{2}}{d z} &=\frac{2 i d_{\mathrm{eff}} \omega_{2}^{2}}{k_{2} c^{2}} A_{3} A_{1}^{*} e^{-i \Delta k z} \end{aligned} }[/math]

Зависимость интенсивности второй гармоники на расстоянии L от разности [math]\displaystyle{ \Delta k }[/math]. При [math]\displaystyle{ \Delta k=0 }[/math] достигается условие фазового синхронизма и интенсивность максимальна

где [math]\displaystyle{ \Delta k = k_1+k_2-k_3 }[/math].

При низком коэффициенте преобразования ([math]\displaystyle{ A_3 \lt \lt A_1, A_2 }[/math]) амплитуды [math]\displaystyle{ A_1 }[/math] и [math]\displaystyle{ A_2 }[/math] можно считать постоянными по всей длине взаимодействия, [math]\displaystyle{ L }[/math]. Учитывая граничные условия[math]\displaystyle{ E_3(z = 0) = 0 }[/math], получим:

[math]\displaystyle{ A_{3}(L)=\frac{2 i d_{\mathrm{eff}} \omega_{3}^{2} A_{1} A_{2}}{k_{3} c^{2}} \int_{0}^{L} e^{i \Delta k z} d z=\frac{2 i d_{\mathrm{eff}} \omega_{3}^{2} A_{1} A_{2}}{k_{3} c^{2}}\left(\frac{e^{i \Delta k L}-1}{i \Delta k}\right) }[/math]

Тогда интенсивность:

[math]\displaystyle{ I_i = 2n_i\varepsilon_0c|A_i|^2 }[/math]

[math]\displaystyle{ I_{3}=\frac{2 d_{\mathrm{eff}}^{2} \omega_{3}^{2} }{n_{1} n_{2} n_{3} \varepsilon_{0} c^{3}} L^{2} \operatorname{sinc}^{2}\left(\frac{\Delta k L}{2}\right)I_{1} I_{2} }[/math]

для второй гармоники

[math]\displaystyle{ I(2\omega) =\frac{2\omega^2 d^2_\text{eff} L^2}{n_{2\omega} n_\omega^2 c^3 \varepsilon_0} \operatorname{sinc}^{2}\left(\frac{\Delta k L}{2}\right) I^2(\omega) }[/math]

При выполнении условия фазового синхронизма [math]\displaystyle{ \Delta k=0 }[/math] интенсивность максимальна и растет как [math]\displaystyle{ z^2 }[/math].

Решение с учётом истощения волны накачки

Когда преобразование во 2-ю гармонику становится значительным, необходимо учитывать истощение волны накачки^[5]^[6]^[7]. Аналогично предыдущему параграфу, уравнения на амплитуды запишутся как

[math]\displaystyle{ \frac{d A_{1}}{d z}=\frac{2 i \omega_{1}^{2} d_{\mathrm{eff}}}{k_{1} c^{2}} A_{2} A_{1}^{*} e^{-i \Delta k z} }[/math]

[math]\displaystyle{ \frac{d A_{2}}{d z}=\frac{i \omega_{2}^{2} d_{\mathrm{eff}}}{k_{2} c^{2}} A_{1}^{2} e^{i \Delta k z} }[/math]

где * означает комплексно-сопряженную величину, при этом [math]\displaystyle{ A_2 }[/math] — амплитуда второй гармоники, а [math]\displaystyle{ A_1 }[/math] — амплитуда фундаментальной волны, [math]\displaystyle{ \omega_2=2\omega_1=2\omega }[/math].

Для простоты предположим, что [math]\displaystyle{ \Delta k=0 }[/math]

Запишем следствие cоотношений Мэнли — Роу

[math]\displaystyle{ n_2|A_2|^2 + n_1|A_1|^2 = n_1 |A_0|^2 }[/math] , так как суммарная интенсивность [math]\displaystyle{ I_1+I_2=I=2 n_1\varepsilon_0 c |A_0|^2 }[/math]

При этом амплитуды представимы в виде:

[math]\displaystyle{ \begin{align} A_1 &= |A_1| e^{i\varphi_1} \\ A_2 &= |A_2| e^{i\varphi_2} \end{align} }[/math]

Амплитуда второй гармоники при распространении в нелинейной среде в зависимости от расстояния. Обозначения см. в статье J. A. Armstrong^[8]. [math]\displaystyle{ \Delta s=0 }[/math] соответствует условию фазового синхронизма.

Подставив соотношения на амплитуды во второе уравнение, получаем

[math]\displaystyle{ \frac{d |A_2| }{d z}e^{i\varphi_2}=\frac{i \omega_{2}^{2} d_{\mathrm{eff}}}{k_{2} c^{2}}\frac{n_2}{n_1}\left(\frac{n_{1}}{n_2} |A_0|^2-|A_2|^2 \right)e^{2i\varphi_1} }[/math]

[math]\displaystyle{ \int_0^{|A_2|_{z=L}} {\frac{d |A_2|}{\frac{n_{1}}{n_2} |A_0|^2-|A_2|^2}} = \int_0^L {\frac{i \omega_{2}^{2} d_{\mathrm{eff}}}{k_{2} c^{2}}\frac{n_2}{n_1} e^{2i\varphi_1- i\varphi_2} dz} }[/math]

Используя

[math]\displaystyle{ \int{\frac{dx}{a^2 - x^2}} = \frac{1}{a}\operatorname{th}^{-1}{\frac{x}{a}} }[/math]

Получим

[math]\displaystyle{ |A_2|_{z=L} = \sqrt{\frac{n_1}{n_2}}|A_0|\operatorname{th}\left(\sqrt{\frac{n_1}{n_2}}|A_0| {\frac{i \omega_{2}^{2} d_{\mathrm{eff}}}{k_{2} c^{2}}\frac{n_2}{n_1} e^{2i\varphi_1- i\varphi_2} L}\right) }[/math]

Предположим, что начальные фазы таковы, что [math]\displaystyle{ e^{2i\varphi_1- i\varphi_2} = -i }[/math], тогда

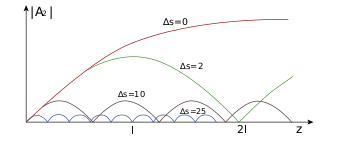
[math]\displaystyle{ |A_2|_{z=L} = \sqrt{\frac{n_1}{n_2}}|A_0|\operatorname{th}\left(L/l\right) }[/math]

где

[math]\displaystyle{ l=\frac{\sqrt{n_1 n_2}c}{|A_0|\omega_{2}d_{\mathrm{eff}}} }[/math]

[math]\displaystyle{ I(2\omega, L) = I(\omega, 0) \operatorname{th}^2{\left( \frac{|A_0|\omega_{2}d_{\mathrm{eff}}L}{\sqrt{n_1 n_2}c} \right) } }[/math]

[math]\displaystyle{ I(\omega, L) = I(\omega, 0)\operatorname{sch}^2{\left( \frac{|A_0|\omega_{2}d_{\mathrm{eff}}L}{\sqrt{n_1 n_2}c} \right) } }[/math]

В общем случае отсутствия фазового синхронизма решение приведено в статье^[8]и дается эллиптическими интегралами.

Механизм возникновения явления

При падении электромагнитной волны небольшой амплитуды на диэлектрик суммарный дипольный момент единицы объёма (поляризованность диэлектрика), возникающий при этом, пропорционален амплитуде волны. В результате дипольный момент рождает вторичную волну той же частоты. При больших амплитудах суммарный дипольный момент является нелинейной функцией амплитуды падающей волны. То есть он оказывается зависящим не только от первой, но и от второй, третьей и последующих степеней амплитуды падающей волны. Это и приводит к рождению вторичных волн удвоенной, утроенной и т. д. частоты (из тригонометрии известно, что [math]\displaystyle{ \cos^{2}\omega t = (1 + \cos 2\omega t)/2, }[/math] [math]\displaystyle{ \cos^{3}\omega t = (3 \cos \omega t + \cos 3 \omega t)/4, }[/math] и т. д.^[9]).

С точки зрения квантовой механики

С квантовой точки зрения нелинейный процесс преобразования частоты выглядит следующим образом. При генерации второй гармоники, можно считать, что два фотона исходной частоты [math]\displaystyle{ \omega }[/math] одновременно поглощаются в среде, переводя систему на виртуальный уровень с энергией [math]\displaystyle{ 2\hbar\omega }[/math], после чего система релаксирует с этого уровня в основное состояние с излучением фотона частотой [math]\displaystyle{ 2\omega }[/math].

Применение

В исследованиях по направлению лазерного термоядерного синтеза используют ГВГ, поскольку критическая плотность плазмы прямо пропорциональна квадрату частоты воздействующего излучения, то увеличение частоты излучения приводит к повышению значения критической плотности плазмы, следовательно, воздействующее излучение взаимодействует с более плотными слоями плазмы. Также использование излучения оптических гармоник позволяет изолировать лазер от отраженного плазмой излучения и тем самым предотвратить разрушение оптических элементов. Использование оптических гармоник применяется для зондирования плазмы. Помимо этого, ГВГ используется для накачки других лазеров и расширения спектра многоспектральных лазерных установок.

Материалы, использующиеся для генерации второй гармоники

Кристаллическая решетка таких материалов не обладает центром инверсии. Так, например, вода, стекло, кристаллы с кубической симметрией не могут генерировать вторую гармонику в объёме.

Здесь приводятся некоторые типы кристаллов, использующихся с определёнными типами лазеров для генерации второй гармоники:

Фундаментальная волна на 600—1500 нм:^[10] BiBO (BiB₃O₆)
Фундаментальная волна на 570-4000 нм:^[11] Иодат лития LiIO₃.
Фундаментальная волна на 800—1100, часто 860 или 980 нм:^[12] Ниобат калия KNbO₃
Фундаментальная волна на 410—2000 нм : BBO (β-BaB₂O₄)^[13]
Фундаментальная волна на 984 нм-3400 нм: KTP (KTiOPO₄) or KTA,^[14]
Фундаментальная волна на 1 064 нм : Дигидроортофосфат калия KDP (KH₂PO₄), Триборат лития (LiB₃O₅), CsLiB₆O₁₀ и Борат бария BBO(β-BaB₂O₄).
Фундаментальная волна на 1 319 нм : KNbO₃, BBO (β-BaB₂O₄), Дигидроортофосфат калия KDP (KH₂PO₄), LiIO₃, LiNbO₃, и Титанил-Фосфат Калия KTP (KTiOPO₄).
Фундаментальная волна на ~1000-2000 нм : кристалы для обеспечения квази-фазового синхронизма, такие как, PPLN.^[15]

Примечательно, что нитевидные биологические белки с цилиндрической симметрией, такие как коллаген, тубулин или миозин, а также некоторые углеводы (такие как крахмал или целлюлоза) также являются довольно хорошими преобразователями во вторую гармонику (накачка в ближней инфракрасной области). ^[16]

Где наблюдается

В сегнетоэлектриках с большой поляризуемостью. Потенциальная яма для электрона там сильно несимметрична. Поэтому сегнетоэлектрик со спонтанной поляризацией много эффективнее преобразует частоту излучения, чем другие кристаллы. Также наблюдается в полимерах, содержащих в своём объёме молекулы с нелинейно-оптическими хромофорами — они также обладают большой поляризуемостью.

Литература

Бурсиан, Э. В. Сегнетоэлектрики в нелинейной оптике // Соросовский образовательный журнал. — 2001. — Т. 7. — С. 98—102.

Примечания

↑ P. A. Franken, A. E. Hill, C. W. Peters, G. Weinreich. Generation of Optical Harmonics // Physical Review Letters. — 1961-08-15. — Т. 7, вып. 4. — С. 118—119. — doi:10.1103/PhysRevLett.7.118.
↑ J. A. Giordmaine. Mixing of Light Beams in Crystals // Physical Review Letters. — 1962-01-01. — Т. 8, вып. 1. — С. 19—20. — doi:10.1103/PhysRevLett.8.19.
↑ P. D. Maker, R. W. Terhune, M. Nisenoff, C. M. Savage. Effects of Dispersion and Focusing on the Production of Optical Harmonics // Physical Review Letters. — 1962-01-01. — Т. 8, вып. 1. — С. 21—22. — doi:10.1103/PhysRevLett.8.21.
↑ Robert C. Miller, Albert Savage. Harmonic Generation and Mixing of CaW${\mathrm{O}}_{4}$: ${\mathrm{Nd}}^{3+}$ and Ruby Pulsed Laser Beams in Piezoelectric Crystals // Physical Review. — 1962-12-01. — Т. 128, вып. 5. — С. 2175—2179. — doi:10.1103/PhysRev.128.2175.
↑ ^5,0 ^5,1 R. W. Boyd (2008). Nonlinear Optics (Third ed.). Orlando: Academic Press.
↑ Zernike, Frits; Midwinter, John E. Applied Nonlinear Optics. — John Wiley & Sons Inc., 1973. — ISBN 0-486-45360-X.
↑ Мидвинтер, Дж.; Цернике, Ф.; «Прикладная нелинейная оптика» Изд-во: М.: Мир, 1976 г.
↑ ^8,0 ^8,1 J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan Phys. Rev. 127, 1918 — Published 15 September 1962
↑ Справочник для студентов технических вузов: высшая математика: физика: теоретическая механика: сопротивление материалов. / А. Д. Полянин, В. Д. Полянин, В. А. Попов и др., 3-е изд., М., АСТ: Астрель, 2005. — 735 с. ил., ISBN 5-17-030740-3 (ООО «Издательство АСТ»), ISBN 5-271-11602-6 (ООО «Издательство Астрель») Приложения, 1. Элементарные функции и их свойства, 1.1 Тригонометрические функции, с. 628—629.
↑ BiBO Crystals (неопр.). newlightphotonics.com. Дата обращения: 1 ноября 2019. Архивировано 16 апреля 2019 года.
↑ LiIO3 crystals - Lithium Iodate Crystal (неопр.). shalomeo.com. Дата обращения: 1 ноября 2019. Архивировано 11 ноября 2019 года.
↑ KNbO3 (неопр.). laser-crylink.com. Дата обращения: 1 ноября 2019. Архивировано 28 июля 2020 года.
↑ BBO Crystals (неопр.). newlightphotonics.com. Дата обращения: 1 ноября 2019. Архивировано 11 сентября 2019 года.
↑ KTP Crystals (неопр.). unitedcrystals.com. Дата обращения: 1 ноября 2019. Архивировано 28 июля 2020 года.
↑ Meyn, J.-P.; Laue, C.; Knappe, R.; Wallenstein, R.; Fejer, M.M. Fabrication of periodically poled lithium tantalate for UV generation with diode lasers (англ.) // Applied Physics B^[англ.] : journal. — 2001. — Vol. 73, no. 2. — P. 111—114. — doi:10.1007/s003400100623. — Bibcode: 2001ApPhB..73..111M.
↑ Francesco S.; Paul J. Second Harmonic Generation Imaging, 2nd edition (англ.). — CRC Taylor&Francis, 2016. — ISBN 978-1-4398-4914-9.

[1] P. A. Franken, A. E. Hill, C. W. Peters, G. Weinreich. Generation of Optical Harmonics // Physical Review Letters. — 1961-08-15. — Т. 7, вып. 4. — С. 118—119. — doi:10.1103/PhysRevLett.7.118.

[2] J. A. Giordmaine. Mixing of Light Beams in Crystals // Physical Review Letters. — 1962-01-01. — Т. 8, вып. 1. — С. 19—20. — doi:10.1103/PhysRevLett.8.19.

[3] P. D. Maker, R. W. Terhune, M. Nisenoff, C. M. Savage. Effects of Dispersion and Focusing on the Production of Optical Harmonics // Physical Review Letters. — 1962-01-01. — Т. 8, вып. 1. — С. 21—22. — doi:10.1103/PhysRevLett.8.21.

[4] Robert C. Miller, Albert Savage. Harmonic Generation and Mixing of CaW${\mathrm{O}}_{4}$: ${\mathrm{Nd}}^{3+}$ and Ruby Pulsed Laser Beams in Piezoelectric Crystals // Physical Review. — 1962-12-01. — Т. 128, вып. 5. — С. 2175—2179. — doi:10.1103/PhysRev.128.2175.

[boyd-5] 5,0 ^5,1 R. W. Boyd (2008). Nonlinear Optics (Third ed.). Orlando: Academic Press.

[6] Zernike, Frits; Midwinter, John E. Applied Nonlinear Optics. — John Wiley & Sons Inc., 1973. — ISBN 0-486-45360-X.

[7] Мидвинтер, Дж.; Цернике, Ф.; «Прикладная нелинейная оптика» Изд-во: М.: Мир, 1976 г.

[armst-8] 8,0 ^8,1 J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan Phys. Rev. 127, 1918 — Published 15 September 1962

[9] Справочник для студентов технических вузов: высшая математика: физика: теоретическая механика: сопротивление материалов. / А. Д. Полянин, В. Д. Полянин, В. А. Попов и др., 3-е изд., М., АСТ: Астрель, 2005. — 735 с. ил., ISBN 5-17-030740-3 (ООО «Издательство АСТ»), ISBN 5-271-11602-6 (ООО «Издательство Астрель») Приложения, 1. Элементарные функции и их свойства, 1.1 Тригонометрические функции, с. 628—629.

[10] BiBO Crystals (неопр.). newlightphotonics.com. Дата обращения: 1 ноября 2019. Архивировано 16 апреля 2019 года.

[11] LiIO3 crystals - Lithium Iodate Crystal (неопр.). shalomeo.com. Дата обращения: 1 ноября 2019. Архивировано 11 ноября 2019 года.

[12] KNbO3 (неопр.). laser-crylink.com. Дата обращения: 1 ноября 2019. Архивировано 28 июля 2020 года.

[13] BBO Crystals (неопр.). newlightphotonics.com. Дата обращения: 1 ноября 2019. Архивировано 11 сентября 2019 года.

[14] KTP Crystals (неопр.). unitedcrystals.com. Дата обращения: 1 ноября 2019. Архивировано 28 июля 2020 года.

[15] Meyn, J.-P.; Laue, C.; Knappe, R.; Wallenstein, R.; Fejer, M.M. Fabrication of periodically poled lithium tantalate for UV generation with diode lasers (англ.) // Applied Physics B^[англ.] : journal. — 2001. — Vol. 73, no. 2. — P. 111—114. — doi:10.1007/s003400100623. — Bibcode: 2001ApPhB..73..111M.

[16] Francesco S.; Paul J. Second Harmonic Generation Imaging, 2nd edition (англ.). — CRC Taylor&Francis, 2016. — ISBN 978-1-4398-4914-9.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]