Алгоритм Карацубы

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис

Умножение Карацубы — метод быстрого умножения, который позволяет перемножать два n-значных числа с битовой вычислительной сложностью:

[math]\displaystyle{ T(n)=O(n^{\log_23}),\quad\log_23=1{,}5849\ldots }[/math].

Изобретён Анатолием Карацубой в 1960 году. Является исторически первым алгоритмом умножения, превосходящим тривиальный по асимптотической сложности[1][2][3][4].

История

В 1960 году Андрей Колмогоров проводил семинар, посвящённый математическим задачам кибернетики. Одной из рассматриваемых на семинаре задач стало умножение двух [math]\displaystyle{ n }[/math]-разрядных целых чисел. Основным известным методом умножения в то время было умножение «в столбик», которое при алгоритмической реализации требовало [math]\displaystyle{ O(n^2) }[/math] элементарных операций (сложений или умножений одноразрядных чисел). Колмогоров выдвинул гипотезу, что умножение «в столбик» является оптимальным алгоритмом умножения двух чисел в том смысле, что время работы любого метода умножения не меньше [math]\displaystyle{ n^2 }[/math] по порядку величины. На правдоподобность «гипотезы [math]\displaystyle{ n^2 }[/math]» указывало то, что метод умножения «в столбик» известен не менее четырёх тысячелетий, и если бы был более быстрый метод умножения, то он, вероятно, уже был бы найден. Однако, через неделю 23-летний Анатолий Карацуба[5][6][7][8] предложил новый метод умножения двух [math]\displaystyle{ n }[/math]-значных чисел с оценкой времени работы [math]\displaystyle{ O(n^{\log_23}) }[/math] и тем самым опроверг «гипотезу [math]\displaystyle{ n^2 }[/math]».

Метод Карацубы относится к алгоритмам вида «разделяй и властвуй», наравне с такими алгоритмами как двоичный поиск, быстрая сортировка и др. Формулы рекурсивного сведения, используемые в методе Карацубы, были известны ещё Чарльзу Бэббиджу, который, однако, не обратил внимания на возможность использования лишь трёх рекурсивных умножений вместо четырёх[9].

Описание метода

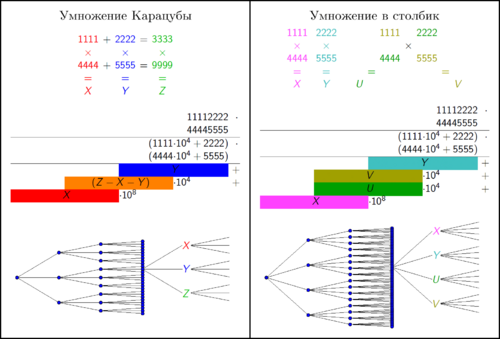
Сравнение алгоритма Карацубы и умножения в столбик. Внизу схематически показано дерево рекурсивных вызовов алгоритма для всё меньших и меньших чисел. Количество вершин на последнем его уровне соответствует количеству элементарных умножений. Очевидно, что у алгоритма Карацубы ширина дерева растёт значительно медленнее.

Два [math]\displaystyle{ n }[/math]-битовых числа можно представить в виде [math]\displaystyle{ ax+b }[/math], [math]\displaystyle{ cx+d }[/math], где [math]\displaystyle{ x=2^{\lceil{n/2}\rceil} }[/math]; [math]\displaystyle{ a,b,c,d \lt 2^{\lceil{n/2}\rceil} }[/math].

Умножение на [math]\displaystyle{ 2^{\lceil{n/2}\rceil} }[/math] (битовый сдвиг) и сложение делаются за постоянное время [math]\displaystyle{ O(1) }[/math]. Поэтому задача умножения сводится к вычислению коэффициентов многочлена [math]\displaystyle{ (ax+b)(cx+d) }[/math]. Используя тождество

[math]\displaystyle{ {\color{green} (a+b)(c+d)} = {\color{red} ac} + {\color{darkorange} (ad + bc)} + {\color{blue} bd}\ , }[/math]

этот многочлен можно представить в виде

[math]\displaystyle{ (ax+b)(cx+d) = {\color{red} ac} x^2 + {\color{darkorange} (ad + bc)} x + {\color{blue} bd} = }[/math]
[math]\displaystyle{ = {\color{red} ac} x^2 + {\color{darkorange} \Big(}{ {\color{green} (a+b)(c+d)} - {\color{red} ac} - {\color{blue} bd} }{\color{darkorange} \Big)} x + {\color{blue} bd}\ . }[/math]

В последнем выражении участвуют три произведения [math]\displaystyle{ \left({ \left\lceil{\frac{n}{2}}\right\rceil+1 }\right) }[/math]-значных чисел. Если вычислять каждое из них по той же схеме, получится алгоритм с рекуррентной оценкой времени работы

[math]\displaystyle{ T(n) = 3 T \left({ \frac{n}{2} }\right) + O(n) = O(n^{\log_2 3})\ . }[/math]

Для сравнения, аналогичный алгоритм, производящий отдельно все четыре умножения [math]\displaystyle{ ac }[/math], [math]\displaystyle{ ad }[/math], [math]\displaystyle{ bc }[/math], [math]\displaystyle{ bd }[/math], требовал бы обычного времени

[math]\displaystyle{ T(n) = 4 T \left({ \frac{n}{2} }\right) + O(n) = O(n^{\log_2 4}) = O(n^2)\ . }[/math]

Примеры

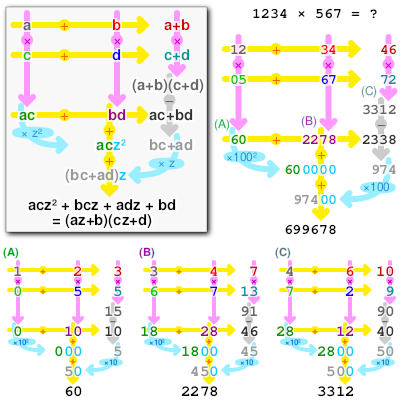
Графическая иллюстрация другого примера: умножения 1234 на 567 по алгоритму Карацубы. Сначала выполняются нижние шаги [math]\displaystyle{ (A),\ (B),\ (C) }[/math], а потом их результаты подставляются в верхнюю схему.

Для удобства изложения будем использовать десятичную систему, то есть аргументы многочлена вида [math]\displaystyle{ x=10^k }[/math] вместо [math]\displaystyle{ x=2^k }[/math]. Цветовая разметка цифр не связана с предыдущим разделом, а обозначает лишь, из какого числа вычленяется та или иная часть.

Вычислим [math]\displaystyle{ {\color{red} 1213} \cdot {\color{blue} 2311} }[/math]:

  • заметим, что [math]\displaystyle{ {\color{red} 12}+{\color{red} 13}=25,\ {\color{blue} 23}+{\color{blue} 11}=34 }[/math] и вычислим [math]\displaystyle{ {\color{darkorange} 25} \cdot {\color{magenta} 34} }[/math]:
    • заметим, что [math]\displaystyle{ {\color{darkorange} 2}+{\color{darkorange} 5}=7,\ {\color{magenta} 3}+{\color{magenta} 4}=7 }[/math] и вычислим [math]\displaystyle{ 7 \cdot 7 = 49 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 2} \cdot {\color{magenta} 3} = 6 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 5} \cdot {\color{magenta} 4} = 20 }[/math]
    • складывая результаты, получим, что [math]\displaystyle{ {\color{darkorange} 25} \cdot {\color{magenta} 34} = 6 \cdot 10^2 + (49 - 6 - 20) \cdot 10 + 20 = 850 }[/math]
  • вычислим [math]\displaystyle{ {\color{red} 12} \cdot {\color{blue} 23} }[/math] как [math]\displaystyle{ {\color{darkorange} 12} \cdot {\color{magenta} 23} }[/math]:
    • заметим, что [math]\displaystyle{ {\color{darkorange} 1}+{\color{darkorange} 2}=3,\ {\color{magenta} 2}+{\color{magenta} 3}=5 }[/math] и вычислим [math]\displaystyle{ 3 \cdot 5 = 15 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 1} \cdot {\color{magenta} 2} = 2 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 2} \cdot {\color{magenta} 3} = 6 }[/math]
    • складывая результаты, получим, что [math]\displaystyle{ {\color{darkorange} 12} \cdot {\color{magenta} 23} = 2 \cdot 10^2 + (15 - 2 - 6) \cdot 10 + 6 = 276 }[/math]
  • вычислим [math]\displaystyle{ {\color{red} 13} \cdot {\color{blue} 11} }[/math] как [math]\displaystyle{ {\color{darkorange} 13} \cdot {\color{magenta} 11} }[/math]:
    • заметим, что [math]\displaystyle{ {\color{darkorange} 1}+{\color{darkorange} 3}=4,\ {\color{magenta} 1}+{\color{magenta} 1}=2 }[/math] и вычислим [math]\displaystyle{ 4 \cdot 2 = 8 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 1} \cdot {\color{magenta} 1} = 1 }[/math]
    • вычислим [math]\displaystyle{ {\color{darkorange} 3} \cdot {\color{magenta} 1} = 3 }[/math]
    • складывая результаты, получим, что [math]\displaystyle{ {\color{darkorange} 13} \cdot {\color{magenta} 11} = 1 \cdot 10^2 + (8 - 1 - 3) \cdot 10 + 3 = 143 }[/math]
  • складывая результаты, получим, что [math]\displaystyle{ {\color{red} 1213} \cdot {\color{blue} 2311} = 276 \cdot 10^4 + (850-276-143) \cdot 10^2 + 143 = 2803243 }[/math]

Примечания

  1. ↑ На практике алгоритм становится эффективнее обычного умножения при умножении чисел длиной порядка сотен двоичных (десятков десятичных) разрядов, на числах меньшей длины алгоритм не даёт существенного преимущества из-за большего, чем в наивном алгоритме, числа требуемых сложений, вычитаний и сдвигов.
  2. ↑ С. А. Гриценко, Е. А. Карацуба, М. А. Королёв, И. С. Резвякова, Д. И. Толев, М. Е. Чанга. Научные достижения Анатолия Алексеевича Карацубы // Математика и информатика, 1, К 75-летию со дня рождения Анатолия Алексеевича Карацубы, Совр. пробл. матем., 16, МИАН, М., 2012, 7–30.
  3. ↑ Карацуба Е. А. Быстрые алгоритмы и метод БВЕ Архивная копия от 4 ноября 2012 на Wayback Machine, 2008.
  4. ↑ Алексеев В. Б. От метода Карацубы для быстрого умножения чисел к быстрым алгоритмам для дискретных функций // Тр. МИАН. — 1997. — Т. 218. — С. 20–27.
  5. ↑ Карацуба А., Офман Ю. Умножение многозначных чисел на автоматах // Доклады Академии Наук СССР. — 1962. — Т. 145, № 2.
  6. ↑ Karacuba A. Berechnungen und die Kompliziertheit von Beziehungen (нем.) // Elektronische Informationsverarbeitung und Kybernetik. — 1975. — Bd. 11.
  7. ↑ Карацуба А. А. Сложность вычислений // Тр. МИАН. — 1995. — Т. 211. — С. 186–202.
  8. ↑ Кнут Д. Искусство программирования. — 3-е изд. — М.: Вильямс, 2007. — Т. 2. Получисленные алгоритмы. — 832 с. — ISBN 0-201-89684-2.
  9. ↑ А. Шень. Gauss multiplication trick? // Математическое Просвещение. — 2019. — Т. 24.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Алгоритм_Карацубы&oldid=5865257