Дерево (теория графов)

Дерево — это связный ациклический граф. Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.

Лес — множество деревьев.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

Связанные определения

• Степень вершины — количество инцидентных ей ребер.

• Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).

• Узел ветвления — неконцевой узел.

• Дерево с отмеченной вершиной называется корневым деревом.
  • [math]\displaystyle{ m }[/math]-й ярус дерева [math]\displaystyle{ T }[/math] — множество узлов дерева, на уровне [math]\displaystyle{ m }[/math] от корня дерева.
  • частичный порядок на вершинах: [math]\displaystyle{ u \prec v }[/math], если вершины [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math] различны и вершина [math]\displaystyle{ u }[/math] лежит на (единственной!) элементарной цепи, соединяющей корень с вершиной [math]\displaystyle{ v }[/math].
  • корневое поддерево с корнем [math]\displaystyle{ v }[/math] — подграф [math]\displaystyle{ \{v\}\cup\{w\mid v\lt w\} }[/math].
  • В контексте, где дерево предполагается имеющим корень, дерево без выделенного корня называется свободным.

• Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:

1. уровень корня дерева [math]\displaystyle{ T }[/math] равен 0;
2. уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева [math]\displaystyle{ T }[/math], содержащего данный узел.

• Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

• Несводимым называется дерево, в котором нет вершин степени 2.

• Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
• Центроид — вершина, при удалении которой размеры получившихся компонент связности не превышают [math]\displaystyle{ \dfrac{n}{2} }[/math] (половины размера исходного дерева)

Двоичное дерево

Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.

Термин двоичное дерево (применяется так же термин бинарное дерево) имеет несколько значений:

• Неориентированное дерево, в котором степени вершин не превосходят 3.
• Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
• Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.

N-арные деревья

N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.

• N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
• N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.

Свойства

• Дерево не имеет кратных рёбер и петель.
• Любое дерево с [math]\displaystyle{ n }[/math] вершинами содержит [math]\displaystyle{ n-1 }[/math] ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда [math]\displaystyle{ B-P=1 }[/math], где [math]\displaystyle{ B }[/math] — число вершин, [math]\displaystyle{ P }[/math] — число рёбер графа.
• Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственной простой цепью.
• Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.
• Любое дерево является двудольным графом.
• Любое дерево, множество вершин которого не более чем счётное, является планарным графом.
• Для любых трёх вершин дерева, пути между парами этих вершин имеют ровно одну общую вершину.

Подсчёт деревьев

Основная статья: Теорема Кэли о числе деревьев

• Число различных деревьев, которые можно построить на [math]\displaystyle{ n }[/math] нумерованных вершинах, равно [math]\displaystyle{ n^{n-2} }[/math] (Теорема Кэли).
• Производящая функция

[math]\displaystyle{ T(z)=\sum_{n=1}^\infty T_nz^n }[/math]

для числа [math]\displaystyle{ T_n }[/math] неизоморфных корневых деревьев с [math]\displaystyle{ n }[/math] вершинами удовлетворяет функциональному уравнению

[math]\displaystyle{ T(z)=z\exp\sum_{r=1}^\infty\frac1r T(z^r) }[/math].

• Производящая функция

[math]\displaystyle{ t(z)=\sum_{n=1}^\infty t_nz^n }[/math]

для числа [math]\displaystyle{ t_n }[/math] неизоморфных деревьев с [math]\displaystyle{ n }[/math] вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:

[math]\displaystyle{ t(z)=T(z)-\frac12\left(T^2(z)-T(z^2)\right). }[/math]

• При [math]\displaystyle{ n\to\infty }[/math] верна следующая асимптотика

[math]\displaystyle{ t_n\sim C\alpha^n/n^{5/2} }[/math]

где [math]\displaystyle{ C }[/math] и [math]\displaystyle{ \alpha }[/math] определённые константы, [math]\displaystyle{ C=0,534948... }[/math], [math]\displaystyle{ \alpha=2,95576... }[/math].

Кодирование деревьев

• Дерево можно кодировать наборами из нулей и единиц. Рассмотрим, например, укладку дерева на плоскости. Начиная с какой-либо вершины будем двигаться по ребрам дерева, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах дерева. Проходя по некоторому ребру, записываем [math]\displaystyle{ 0 }[/math] при движении по ребру в первый раз и [math]\displaystyle{ 1 }[/math] при движении по ребру второй раз (в обратном направлении). Если [math]\displaystyle{ m }[/math] — число рёбер дерева, то через [math]\displaystyle{ 2m }[/math] шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из [math]\displaystyle{ 0 }[/math] и [math]\displaystyle{ 1 }[/math] (код дерева) длины [math]\displaystyle{ 2m }[/math] позволяет однозначно восстанавливать не только само дерево [math]\displaystyle{ D }[/math], но и его укладку на плоскости. Произвольному дереву соответствуют несколько таких кодов. В частности, из этого способа кодирования вытекает следующая грубая оценка на число деревьев с [math]\displaystyle{ n }[/math] вершинами:

  [math]\displaystyle{ t_n\le T_n\lt 2^{2n} }[/math]

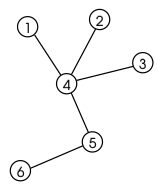
• Код Прюфера сопоставляет произвольному конечному дереву с [math]\displaystyle{ n }[/math] вершинами последовательность из [math]\displaystyle{ n-2 }[/math] чисел от [math]\displaystyle{ 1 }[/math] до [math]\displaystyle{ n }[/math] с возможными повторениями. Например дерево на рисунке имеет код Прюфера (4,4,4,5). Между деpевьями с помеченными вершинами и их кодами Прюфера существует взаимно однозначное соответствие. Из кода Прюфера выводится формула Кэли.

• Дерево можно задать в виде стpоки, содержащей символы, помечающие вершины деpева, а также открывающие и закрывающие кpуглые скобки. Между деpевьями и их линейными скобочными записями существует взаимно однозначное соответствие.

См. также

• Глоссарий теории графов
• Лес непересекающихся множеств
• Список структур данных (деревья)

Литература

• Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4.
• Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
• Харари Ф. Теория графов. — М.: Мир, 1973. — 302 с.