R*-дерево

R* дерево
Год изобретения	1990
Автор	Норберт Бекман, Ганс-Петер Кригель, Ральф Шнайдер и Бернхард Сигер
Сложность в О-символике
В среднем В худшем случае Расход памяти O(n) O(n) Поиск O(log n) Вставка O(log n)

R*-деревья — это вариант R-деревьев, используемый для индексирования пространственной информации. R*-деревья имеют слегка повышенные затраты на создание, чем стандартные R-деревья, так как данные могут требовать переустановки (удаление + вставка), но получающееся дерево обычно имеет лучшую производительность запросов. Подобно стандартному R-дереву, оно может запоминать как точки, так и пространственные данные. Дерево предложили Норберт Бекман, Ганс-Петер Кригель, Ральф Шнайдер и Бернхард Сигер в 1990.

Отличие R*-деревьев и R-деревьев

R*-дерево, построенное путём кратной вставки (в ELKI). Есть небольшое перекрытие в этом дереве, что приводит к хорошей производительности запросов. Красные и синие прямоугольники являются страницами индексов, зелёные прямоугольники являются листьями.

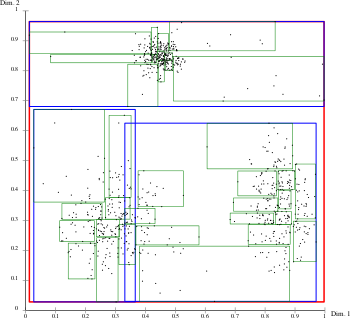
Минимизация как покрытия, так и перекрытия важны для производительности R-деревьев. Перекрытие означает, что при запросах данных или вставке более чем одну ветвь дерева нужно расширять (по причине метода разбиения данных на области, которые могут накладываться). Минимизированное покрытие улучшает удаление, позволяя исключать полные страницы из поиска более часто, в частности, для запросов с отрицательными диапазонами. R*-дерево пытается уменьшить оба значения, используя комбинацию алгоритма разбиения просмотренного узла и концепции принудительной переустановки при переполнении узла. Подход основан на наблюдении, что структуры R-дерева высокочувствительны к порядку, в котором элементы дерева были вставлены, так что структуры на основе вставок (а не на основе массовой загрузки) скорее будут подоптимальными. Удаление и повторная вставка элементов дерева позволяет «найти» им место в дереве, которое будет более пригодно, чем первоначальное их расположение.

Когда узел переполняется, часть его элементов удаляется из узла и устанавливается заново в дерево. (Чтобы избежать бесконечной каскадной переустановки, вызванной переполнением другого узла при этой операции, процедура переустановки может быть вызвана только один раз на каждом уровне дерева при вставке любого нового элемента.) Это приводит к созданию более хорошо кластеризованных групп элементов в узлах, уменьшая покрытие узла. Более того, часто разбиение узла часто откладывается, что приводит к увеличению среднего заполнения узла. Повторную вставку можно рассматривать как метод оптимизации увеличивающегося дерева при переполнении узла.

Производительность

• Улучшенная эвристика разбиения даёт страницы, которые более прямоугольны, а потому лучше приспособлены для многих алгоритмов.
• Метод повторной вставки оптимизирует существующее дерево, но увеличивает сложность.
• Эффективно поддерживает точки и пространственные данные.

• Результаты различных подходов к разбиению на базе данных немецких почтовых отделений
• 

  R-дерево с квадратным разбиением Гутмана .
  Есть много страниц, которые распространяются слева направо через всю Германию и страницы сильно перекрываются. Это не вполне благоприятное свойство для большинства приложений, для которых часто нужны только малые прямоугольные области, пересекающиеся со многими полосами.

• 

  R-дерево с линейным разбиением Анга-Тана.
  Хотя прямоугольники не столь протяжёны, как в разбиении Гутмана, проблема разбиения на полосы действует почти на каждый лист на странице. Страницы листов пересекаются мало, но справочные страницы пересекаются сильно.

• 

  Топологическое разбиение R* дерева.
  Страницы перекрываются очень мало, поскольку R*-дерево пытается минимизировать перекрытые страниц, а повторная вставка далее оптимизирует дерево. Стратегия разбиения также не даёт предпочтения полосам, так что получающиеся страницы более пригодны для картографических приложений.

Алгоритм и сложность

• R*-дерево использует для запросов и операций удаления тот же алгоритм, что и обычное R-дерево.
• Для вставки R*-дерево использует комбинированную стратегию. Для листовых узлов перекрытие минимизировано, в то время как для внутренних узлов минимизируются линейные размеры и площадь.
• Для разбиения R*-дерево использует топологическое разбиение, которое выбирает разбиение осей по периметру, затем минимизируется перекрытие.
• Вдобавок к улучшенной стратегии разбиения R*-дерево пытается избежать разбиения при повторной вставке объектов и поддеревьев в дерево в духе концепции сбалансированного B-дерева.

Запросы в худшем случае и сложность удаления идентичны таким же действиям в R-дереве. Стратегия вставки в R*-дерево имеет сложность [math]\displaystyle{ \mathcal{O}(M \log M) }[/math] и более сложна по сравнению со стратегией линейного разбиения ([math]\displaystyle{ \mathcal{O}(M) }[/math]) R-дерева, но менее сложна по сравнению со стратегией квадратного разбиения ([math]\displaystyle{ \mathcal{O}(M^2) }[/math]) для размера страницы в [math]\displaystyle{ M }[/math] объектов и имеет малый вклад в общую сложность. Полная сложность вставки остаётся сравнимой со сложностью R-дерева: повторная вставка влияет максимум на одну ветку дерева, а потому даёт [math]\displaystyle{ \mathcal{O}(\log n) }[/math] повторных вставок, что сравнимо по производительности с обычным R-деревом. Так что общая сложность R*-дерева совпадает со сложностью обычного R-дерева.

Реализация полного алгоритма должна предусматривать обработку многих угловых случаев и зависимых ситуаций, которые здесь не обсуждаются.