P-волна
Р-волны — упругие продольные волны, вызывающие колебания элементарных частиц упругой среды в направлении распространения волны и создающие в среде объёмные деформации сжатия—растяжения[1](Рисунок 1). Самые быстрые среди объёмных волн, поэтому получили название «P-волны» от латинского «prima» — первичные. Способны распространятся в твердых телах, жидкостях и газах.

Основные свойства
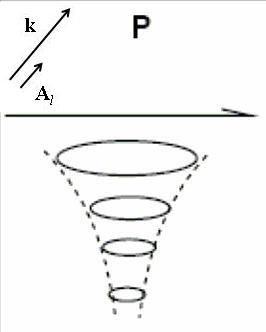
Решение волнового уравнения для плоской гармонической Р-волны:
[math]\displaystyle{ u_p=A\begin{pmatrix} \sin{i} \\ 0 \\ -\cos{i}\end{pmatrix} exp\left(i\omega\left(\frac{\sin{i}}{v_p}x-\frac{\cos{i}}{v_p}z-t\right)\right) }[/math]
Скорость P-волн в однородной изотропной среде равна:
- [math]\displaystyle{ v_p= \sqrt{ \frac {K+\frac{4}{3}G} {\rho}}= \sqrt{ \frac{\lambda+2\mu}{\rho}}= \sqrt{\frac{M}{\rho}}=\sqrt{\frac{E(1-\nu)}{(1+\nu)(1-2\nu)\rho}}, }[/math]
где [math]\displaystyle{ E }[/math] — модуль Юнга, [math]\displaystyle{ \nu }[/math] — коэффициент Пуассона, K — объёмный модуль, [math]\displaystyle{ G }[/math] — модуль сдвига (также обозначаемый как [math]\displaystyle{ \mu }[/math] — второй параметр Ламе), [math]\displaystyle{ \rho }[/math] — плотность среды, через которую проходит волна, [math]\displaystyle{ \lambda }[/math] — первый параметр Ламе, [math]\displaystyle{ M }[/math] — упругий модуль P-волны, определяемый как
[math]\displaystyle{ M = K + \frac{4}{3}G }[/math]Типичные значения для скоростей Р-волн, определяемых при землетрясениях находятся в диапазоне от 5 до 13 км/с, при расчётах должны использоваться адиабатические модули упругости

Преломление Р-волны на границе двух упругих сред
Для анализа волнового поля в реальных средах необходимо учитывать наличие границ между средами с разными упругими постоянными и свободную поверхность. Пусть Р-волна падает из среды 1 в среду 2, что видно на рисунке 4, векторами на рисунке обозначено направление смещения соответствующих волн.

На границе S двух однородных сред получаем два граничных условия
[math]\displaystyle{ \mathbf u(\mathbf r)|_{S_-}= \mathbf u(\mathbf r)|_{S_+}, }[/math][math]\displaystyle{ \hat\sigma{\mathbf n}|_{S_-}= \hat\sigma{\mathbf n}|_{S_+}, }[/math]
где n — вектор нормали к границе S. Первое выражение соответствует непрерывности вектора смещения, а второе отвечает за равенство векторов напряжений с обеих сторон [math]\displaystyle{ S_+ }[/math] и [math]\displaystyle{ S_- }[/math] на границе.
Если Р-волна преломляется на границе, то возникает четыре волны: отражённая и проходящая волна P и отражённая и прошедшая волна SV.
Преломление Р-волны на границе среда-вакуум
В случае, когда упругая среда граничит с вакуумом, вместо двух условий остаётся только одно граничное условие, выражающее тот факт, что давление на границу со стороны вакуума должно равняться нулю:
[math]\displaystyle{ \mathbf u(\mathbf r)|_{S}= 0. }[/math]
Тогда в случае Р-волны, где А — это амплитуда падающей волны, [math]\displaystyle{ c_s }[/math] — скорость поперечной волны в среде, [math]\displaystyle{ c_p }[/math] — скорость продольной волны в среде, i — угол отражения моды P от моды P, j — угол отражения моды S от моды P, получаем[math]\displaystyle{ k_{p s} = A \frac{2 c_p/c_s \sin 2j \cos 2i}{(c_p/c_s)^2 \cos^2 2j +\sin 2j \sin 2i}, }[/math]
[math]\displaystyle{ k_{pp}=-A \frac{(c_p/c_s)^2 \cos^2(2j)- \sin(2 j) \sin(2 i)}{(c_p/c_s)^2 \cos^2(2j)+ \sin(2 j) \sin(2 i)}. }[/math]
[math]\displaystyle{ k_{p s} }[/math] — это коэффициент отражения моды S от моды P, [math]\displaystyle{ k_{pp} }[/math] — это коэффициент отражения моды P от моды P.

Затененная зона P-волн
Сейсмологи обычно измеряют расстояния от эпицентра землетрясения в градусах: расстояние от нужной точки земной поверхности до эпицентра рассматривается в виде угла между направлением из центра Земли на эпицентр и направлением из центра Земли на данную точку. Было замечено, что в диапазоне углов от 103° до 142° от эпицентра P-волны практически незаметны, это затенённая зона P-волн. Как установил Р. Д. Олдхэм[англ.] в 1906 году, это происходит из-за преломления P-волн на границе земного ядра[2].
См. также
Примечания
- ↑ А. Вартанов. Физико-технический контроль и мониторинг при освоении подземного пространства городов. — Litres, 2017-09-26. — 548 с. — ISBN 978-5-04-081643-9. Архивная копия от 15 января 2022 на Wayback Machine
- ↑ Эйби, 1982, с. 37.
Литература
- Ландау Л. Д., Лившиц Е. М. Теория упругости. — Москва: Наука, т. 7, 1965
- Яновская Т. Б. Основы сейсмологии.-ВВМ, 2006
- Аки К.,Ричардс П. Количественная сейсмология: теория и методы.-М.:Мир,1983
- Сейсморазведка. Справочник геофизика./Под ред. И. И. Гурвича, В. П. Номоконова.- Москва: Недра,1981
- Эйби Дж. А. Землетрясения = Earthquakes. — М.: Недра, 1982. — 50 000 экз.