Ядерная оценка плотности

Ядерная оценка плотности 100 нормально распределённых случайных чисел с использованием различных сглаживающих полос пропускания.

Ядерная оценка плотности (ЯОП, англ. Kernel Density Estimation, KDE) — это непараметрический способ оценки плотности случайной величины. Ядерная оценка плотности является задачей сглаживания данных, когда делается заключение о совокупности, основываясь на конечных выборках данных. В некоторых областях, таких как обработка сигналов и математическая экономика, метод называется также методом окна Парзена-Розенблатта. Как считается, Эммануэль Парзен и Мюррей Розенблатт независимо создали метод в существующем виде.

Определение

Пусть [math]\displaystyle{ (x_1, x_2, \dots, x_n) }[/math] является одномерной выборкой независимых одинаково распределённых величин, извлечённых из некоторого распределения с неизвестной плотностью ƒ. Наша задача заключается в оценке формы функции ƒ. Её ядерный оценщик плотности равен

[math]\displaystyle{ \hat{f}_h(x)=\frac{1}{n}\sum_{i=1}^n K_h (x - x_i)=\frac{1}{nh} \sum_{i=1}^n K\Big(\frac{x-x_i}{h}\Big), }[/math]

где K является ядром, то есть неотрицательной функцией, а h > 0 является сглаживающим параметром, называемым шириной полосы. Ядро с индексом h называется взвешенным ядром и определяется как [math]\displaystyle{ K_h(x)=1/h K(x/h) }[/math]. Интуитивно стараются выбрать h как можно меньше, насколько данные это позволяют, однако всегда существует выбор между смещением оценщика и его дисперсией. Выбор полосы пропускания обсуждается более подробно ниже.

Существует ряд наиболее часто используемых ядерных функций: однородная, треугольная, бивзвешенная, тривзвешенная, Епанечникова, нормальная и другие. Ядро Епанечникова оптимально в смысле среднеквадратичной ошибки, хотя потеря эффективности для ядер, перечисленных до него, мала. Вследствие удобных математических свойств часто используется нормальное ядро, среднее которого [math]\displaystyle{ K(x)=\phi(x) }[/math], где [math]\displaystyle{ \phi }[/math] является стандартной нормальной функцией плотности.

Построение ядерной оценки плотности находит интерпретацию в областях за пределами оценки плотности. Например, в термодинамике это эквивалентно количеству теплоты, получающейся, когда ядра оператора теплопроводности (фундаментальные решения уравнения теплопроводности) помещаются в каждой точке данных x_i. Похожие методы используются для построения дискретных операторов Лапласа в точках облака для обучения на основе многообразий.

Ядерные оценки плотности тесно связаны с гистограммами, но могут быть наделены свойствами, такими как гладкость или непрерывность, путём выбора подходящего ядра. Чтобы это увидеть, сравним построение гистограммы и ядерной оценки плотности на этих 6 точках:

1	2	3	4	5	6
-2,1	-1,3	-0,4	1,9	5,1	6,2

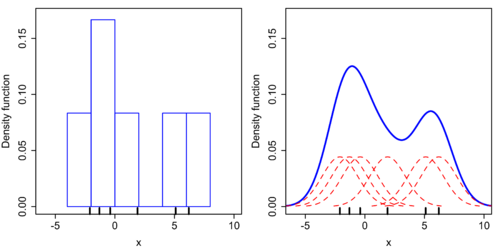
Для гистограммы горизонтальная ось разделена на подинтервалы, которые покрывают область данных. В этом случае мы имеем 6 отрезков, каждая длины 2. Когда точка данных попадает внутрь отрезка, мы помещаем прямоугольник высоты 1/12. Если в отрезок попадает более одной точки, мы размещаем прямоугольники друг над другом.

Для ядерной оценки плотности мы помещаем нормальное ядро с дисперсией 2,25 (показаны красными пунктирными линиями) для каждой точки данных x_i. Ядра суммируются, давая ядерную оценку плотности (сплошная синяя кривая). Гладкость ядерной оценки плотности очевидна при сравнении с дискретностью гистограммы, так как ядерные оценки плотности сходятся быстрее к истинной лежащей в основе плотности для непрерывных случайных величин.

Сравнение гистограммы (слева) и ядерной оценки плотности (справа), построенных из тех же самых данных. 6 индивидуальных ядер показаны красными пунктирными линиями, ядерная оценка плотности показана синей кривой. Точки данных показаны чёрточками на ленточной диаграмме по горизонтальной оси.

Выбор полосы пропускания

Ядерная оценка плотности (ЯОП, англ. Kernel density estimate, KDE) с различными полосами пропускания случайной выборки 100 точек из стандартного нормального распределения.
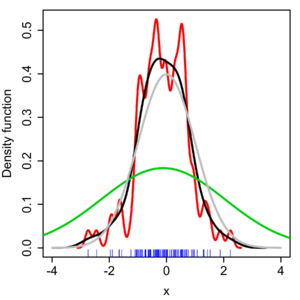
Серая кривая: истинная плотность (стандартное нормальное распределение).
Красная кривая: KDE с h=0,05.
Чёрная кривая: KDE с h=0,337.
Зелёная кривая: KDE с h=2.

Полоса пропускания ядра является свободным параметром, который оказывает сильное влияние на результат оценки. Чтобы показать этот эффект, мы возьмём псевдослучайную выборку из обычного нормального распределения (отражена синими чёрточками на ленточной диаграмме на горизонтальной оси). Серая кривая представляет истинную плотность (нормальная плотность со средним 0 и дисперсией 1). Для сравнения, красная кривая недостаточно сглажена, поскольку она содержит слишком много случайных выбросов, возникающих при использовании полосы пропускания h=0,05, которая слишком мала. Зелёная кривая чрезмерно сглажена, поскольку используемая полоса пропускания h=2 существенно скрывает структуру. Чёрная кривая с полосой пропускания h=0,337 считается оптимально сглаженной, поскольку её оценка плотности близка к истинной плотности.

Наиболее употребительным критерием оптимальности для выбора этого параметра является ожидаемая функция потерь L₂, также называемая средним накопленным квадратом ошибки (англ. Mean Integrated Squared Error, MISE):

[math]\displaystyle{ \operatorname{MISE} (h)=\operatorname{E}\!\left[\, \int (\hat{f}_h(x) - f(x))^2 \, dx \right]. }[/math]

При слабых предположениях о функциях ƒ и K (ƒ в общем случае является неизвестной вещественной функцией плотности), MISE (h)=AMISE(h) + o(1/(nh) + h⁴), где o является «o» малым. AMISE обозначает «Asymptotic MISE» (асимптотическую MISE), которая состоит из двух ведущих членов

[math]\displaystyle{ \operatorname{AMISE}(h)=\frac{R(K)}{nh} + \frac{1}{4} m_2(K)^2 h^4 R(f'') }[/math]

где [math]\displaystyle{ R(g)=\int g(x)^2 \, dx }[/math] для функции g, [math]\displaystyle{ m_2(K)=\int x^2 K(x) \, dx }[/math], а ƒ'' является второй производной от ƒ. Для нахождения значения h_AMISE, где достигается минимум AMISE, необходимо продифференцировать предыдущее выражение для AMISE по h и получить решение [math]\displaystyle{ h_{\operatorname{AMISE}} }[/math] из следующего алгебраического уравнения:

[math]\displaystyle{ \frac{\partial}{\partial h} \operatorname{AMISE}(h)\equiv-\frac{R(K)}{nh^2} + m_2(K)^2 h^3 R(f'')=0 }[/math]

или

[math]\displaystyle{ h_{\operatorname{AMISE}}=\frac{ R(K)^{1/5}}{m_2(K)^{2/5}R(f'')^{1/5} n^{1/5}}. }[/math]

Формулы для вычисления AMISE и h_AMISE не могут быть использованы прямо, поскольку они включают в себя неизвестную функцию плотности ƒ или её вторую производную ƒ'', так что было разработано большое число автоматических, основанных на данных, методов для выбора полосы пропускания. Во многих обзорах сравнивается эффективность этих методов с общим мнением, что подключаемые выборочные функции и функции перекрёстной валидации наиболее полезны над широкой областью множеств данных.

Подстановка любой полосы пропускания h, которая имеет тот же асимптотический порядок n^−1/5 как h_AMISE в AMISE даёт [math]\displaystyle{ \mathrm{AMISE}(h)=O(n^{-4/5}) }[/math], где O — «O» большое. Можно показать, что при слабых предположениях не может существовать непараметрического оценщика, который сходится быстрее, чем ядерный оценщик. Заметим, что скорость n^−4/5 меньше, чем типичная скорость сходимости n⁻¹ параметрических методов.

Если полоса пропускания не фиксирована и может меняться в зависимости от места либо величины оценки (balloon оценщик) или величины выборки (поточечный оценщик), получается мощный метод, называемый методом адаптивной ядерной оценки плотности.

Выбор полосы пропускания для ядерной оценки плотности с медленно убывающим «хвостом» является относительно трудной задачей.

Эмпирическое правило для выбора полосы пропускания

Если используются базовые функции Гаусса для аппроксимации одномерных данных и оцениваемая низлежащая плотность является гауссовой, оптимальный выбор для h (то есть полоса пропускания, минимизирующая средний накопленный квадрат ошибки) равна

[math]\displaystyle{ h=\left(\frac{4\hat{\sigma}^5}{3n}\right)^{\frac{1}{5}} \approx 1,06 \hat{\sigma} n^{-1/5}, }[/math]

где [math]\displaystyle{ \hat{\sigma} }[/math] является среднеквадратическим отклонением выборки. Аппроксимация называется аппроксимацией нормального распределения, гауссовым распределением или эмпирическим правилом Сильвермана (1986). Хотя это эмпирическое правило вычислительно легко применять, его следует применять с осторожностью, так как оно даёт сильно неточные оценки, когда плотность не близка к нормальной. Например, рассмотрим оценку бимодальной гауссовой смеси:

[math]\displaystyle{ \textstyle\frac{1}{2\sqrt{2\pi}}e^{-\frac{1}{2}(x-10)^2}+\frac{1}{2\sqrt{2\pi}}e^{-\frac{1}{2}(x+10)^2} }[/math]

из выборки с 200 точками. Рисунок справа внизу показывает истинную плотность и две ядерные оценки плотности — одна использует эмпирическое правило выбора полосы, а другая использует выбор полосы, основанный на решении уравнения. Оценка на основе эмпирического правила чрезмерно сглажена. Matlab скрипт для примера использует kde.m и дан ниже.

Сравнение между эмпирическим правилом и решением уравнения.

% Data
randn('seed',1)                            % Used for reproducibility
data=[randn(100,1)-10; randn(100,1)+10]; % Смесь двух нормальных распределений
% True
phi=@(x) exp(-.5*x.^2)/sqrt(2*pi);       % Нормальная плотность
tpdf=@(x) phi(x+10)/2+phi(x-10)/2;       % Истинная плотность
% Kernel
h=std(data)*(4/3/numel(data))^(1/5);     % Полоса пропускания по эмпирическому правилу Сильвермана
kernel=@(x) mean(phi((x-data)/h)/h);     % Ядерная плотность
kpdf=@(x) arrayfun(kernel,x);            % Поэлементное применение
% Plot
figure(2), clf, hold on
x=linspace(-25,+25,1000);                % Линейная плотность
plot(x,tpdf(x))                            % График истинной плотности
plot(x,kpdf(x))                            % График ядерной плотности с эмпирическим правилом
kde(data)                                  % График ядерной плотности с решением уравнения для вычисления полосы

Связь с характеристической функцией оценщика плотности

Если дана выборка [math]\displaystyle{ (x_1, x_2, \dots, x_n) }[/math], естественно оценить характеристическую функцию [math]\displaystyle{ \varphi(t)=\mathrm{E}[e^{itX}] }[/math] как

[math]\displaystyle{ \hat\varphi(t)=\frac{1}{n} \sum_{j=1}^n e^{itx_j} }[/math]

Зная характеристическую функцию, можно найти соответствующую плотность вероятности через формулы преобразования Фурье. Имеется одна трудность применения этой формулы обращения, заключающаяся в том, что это приводит к расходящемуся интегралу, поскольку оценка [math]\displaystyle{ \scriptstyle\hat\varphi(t) }[/math] недостоверна для больших t. Чтобы избежать этой проблемы, оценщик [math]\displaystyle{ \scriptstyle\hat\varphi(t) }[/math] умножается на демпфирующую функцию [math]\displaystyle{ \psi_h(t)=\psi(ht) }[/math], которая равна 1 в начале координат, а затем падает до 0 на бесконечности. «Параметр полосы пропускания» h контролирует, насколько мы пытаемся ограничить изменение функции [math]\displaystyle{ \scriptstyle\hat\varphi(t) }[/math]. В частности, когда h мало, [math]\displaystyle{ \psi_h(t) }[/math] будет примерно равно единице для больших t, что означает, что [math]\displaystyle{ \scriptstyle\hat\varphi(t) }[/math] остаётся практически неизменной в наиболее важной области t.

Наиболее употребимым способом выбора функции [math]\displaystyle{ \psi }[/math] является либо однородной функцией [math]\displaystyle{ \psi(t)=\mathbf{1}\{-1 \leqslant t \leqslant 1\} }[/math], которая эффективно означает усечение интервала интегрирования в формуле инвертирования до [−1/h, 1/h], или гауссовой функцией [math]\displaystyle{ \psi(t)=e^{-\pi t^2} }[/math]. Когда функция [math]\displaystyle{ \psi }[/math] выбрана, может быть применена формула инвертирования и оценщиком плотности будет

[math]\displaystyle{ \begin{align} \hat{f}(x) &= \frac{1}{2\pi} \int_{-\infty}^{+\infty} \hat\varphi(t)\psi_h(t) e^{-itx}dt =\frac{1}{2\pi} \int_{-\infty}^{+\infty} \frac{1}{n} \sum_{j=1}^n e^{it(x_j-x)} \psi(ht) dt \\ &= \frac{1}{nh} \sum_{j=1}^n \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-i(ht)\frac{x-x_j}{h}} \psi(ht) d(ht) =\frac{1}{nh} \sum_{j=1}^n K\Big(\frac{x-x_j}{h}\Big), \end{align} }[/math]

где K является преобразованием Фурье демпфирующей функции [math]\displaystyle{ \psi }[/math]. Тогда ядерный оценщик плотности совпадает с характеристической функцией оценщика плотности.

Статистические реализации

Неполный список программного обеспечения, реализующих ядерные оценщики плотности:

• В пакете Analytica релиз 4.4 опция Smoothing для функции плотности вероятности использует KDE, и для выражений возможность доступна как встроенная Pdf функция.
• На языках C/C++ FIGTree является библиотекой, которая может быть использована для вычисления ядерной оценки плотности с помощью нормальных ядер. Доступен MATLAB-интерфейс.
• На языке C++ libagf является библиотекой для адаптивной ядерной оценки плотности.
• В программе CrimeStat ядерная оценка плотности реализована с пятью различными ядерными функциями — нормальная, однородная, четвёртого порядка, отрицательно экспоненциальная и треугольная. Доступны процедуры одно- и двуядерной оценки плотности. Ядерная оценка плотности используется также в интерполяционной процедуре Head Bang, в оценке двухмерной функции плотности Journey-to-crime, и оценке трёхмерной байесовой оценке Journey-to-crime.
• Во фреймворке ELKI ядерные функции плотности можно найти в пакете de.lmu.ifi.dbs.elki.math.statistics.kernelfunctions
• В продуктах компании ESRI ядерное отображение плотности находится в пакете средств Spatial Analyst и использует ядро четвёртого порядка (бивзвешенное).
• Для программы Excel компания «the Royal Society of Chemistry» создала дополнение для выполнения ядерной оценки плотности, базирующееся на Analytical Methods Committee Technical Brief 4 (Техническая сводка 4 Комитета Аналитических методов).
• В gnuplot ядерная оценка плотности реализована опцией smooth kdensity, файл данных может содержать вес и полосу пропускания для каждой точки или полоса пропускания может быть установлена автоматически согласно «эмпирическому правилу Сильвермана» (см. выше).
• В языке Haskell ядерная плотность реализована в пакете statistics.
• В системе IGOR Pro ядерная оценка плотности реализована в виде операции StatsKDE (добавлена в версии Igor Pro 7.00). Полоса пропускания может быть указана или оценена средними Сильвермана, Скотта или Боуманна и Аззалини. Типы ядер: Епанечникова, бивзвешенные, тривзвешенные, треугольные, гауссовы и прямоугольные.
• На языке Java, пакет Weka предоставляет weka.estimators.KernelEstimator среди прочего другого.
• На языке JavaScript пакет визуализации D3.js содержит пакет KDE в пакете science.stats.
• В пакете JMP может быть использовано средство «Distribution platform» для создания одномерной ядерной оценки плотности, а «Fit Y by X platform» может быть использовано для создания двумерной ядерной оценки плотности.
• На языке Julia ядерная оценка плотности реализована в пакете KernelDensity.jl.
• В программе MATLAB ядерная оценка плотности реализована через функцию ksdensity (Statistics Toolbox). В релизе 2018 года MATLAB, могут быть заданы как полоса пропускания, так и ядерный сглаживатель, включая и другие опции, такие как указание пределов ядерной плотности. Альтернативно, бесплатный пакет для MATLAB, который реализует автоматический выбор полосы пропускания, доступен на странице «MATLAB Central File Exchange» для
  • 1-мерных данных
  • 2-мерных данных
  • n-мерных данные
    Бесплатный набор средств для MATLAB с реализацией ядерной регрессии, ядерной оценки плотности, ядерной оценки функции риска и многих других доступен на этой странице (этот набор является частью книги «Kernel Smoothing in MATLAB»).
• В системе Mathematica численная оценка ядерного распределения реализована в виде функции SmoothKernelDistribution здесь, а символьная оценка реализована с помощью функции KernelMixtureDistribution here и обе реализации осуществляют выбор полосы пропускания из представленных данных.
• Для пакета Minitab компания «the Royal Society of Chemistry» создала макро для осуществления ядерной оценки плотности на основе их Analytical Methods Committee Technical Brief 4 (Техническая сводка 4 Комитета Аналитических методов).
• В библиотеке NAG ядерная оценка плотности реализована процедурой g10ba (доступной на языке Fortran и языке C).
• В библиотеке Nuklei методы ядерной плотности на языке C++ фокусируются на дынных из специальной евклидовой группы [math]\displaystyle{ SE(3) }[/math].
• В системе Octave ядерная оценка плотности реализована возможностью kernel_density (пакет математической экономики).
• В пакете Origin 2D ядерный график плотности может быть построен с помощью пользовательского интерфейса пакета, а коды двух функций Ksdensity для 1D и Ks2density для 2D могут быть взяты на языках LabTalk, Python или C.
• На языке Perl реализацию можно найти в модуле Statistics-KernelEstimati
• На языке PHP реализацию можно найти в библиотеке MathPHP
• На языке Python существует множество реализаций: pyqt_fit.kde Module в пакете PyQt-Fit, SciPy (scipy.stats.gaussian_kde и scipy.signal.parzen), Statsmodels (KDEUnivariate и KDEMultivariate) и Scikit-learn (KernelDensity) (см. сравнение). KDEpy поддерживает взвешенные данные, и FFT-реализация на порядок быстрее других реализаций.
• В языке R это реализовано через density в базовой поставке, через bkde в библиотеке KernSmooth, через ParetoDensityEstimation в библиотеке AdaptGauss (для оценки плотности распределения Парето), через kde в библиотеке ks, через dkden и dbckden в библиотеке evmix, npudens в библиотеке np (численные и категоральные данные), sm.density в библиотеке sm. Для получения реализации функции kde.R, которая не требует установки какого-либо пакета или библиотеки, см. kde.R. Библиотека btb, предназначенная для городского анализа, реализует ядерную оценку плотности через kernel_smoothing.
• В системе SAS (программа) может быть использована процедура proc kde для оценки одномерных и двумерных ядерных плотностей.
• В пакете Stata это реализовано в виде kdensity, например histogram x, kdensity. Альтернативно, доступен бесплатный модуль KDENS пакета Stata здесь, который позволяет оценить 1D- или 2D-функции плотности.
• В Apache Spark вы можете использовать класс KernelDensity() (см. официальную документацию)

См. также

• Ядро (статистика)
• Ядерный сглаживатель
• Ядерная регрессия
• Оценка плотности (with presentation of other examples)
• Процедура среднего сдвига
• Многомерная ядерная оценка плотности
• Адаптивная ядерная оценка плотности

Ссылки

• Introduction to kernel density estimation Короткое введение, где объясняется ядерная оценка плотности как усовершенствование гистограмм.
• Kernel Bandwidth Optimization Свободное онлайн средство, которое генерирует оптимизированную ядерную оценку плотности на ваших данных.
• Free Online Software (Calculator) вычисляет ядерную оценку плотности для любой выборки для ядер: гауссово, Епанечникова, прямоугольное, треугольное, бивзвешенное, косинусное и optcosine.
• Kernel Density Estimation Applet Онлайновый интерактивный пример ядерной оценки плотности. Требует версию NET 3.0 или выше.