Теорема Ролля
Теорема Ро́лля (теорема о нуле производной) утверждает, что
|
Если вещественная функция, непрерывная на отрезке [math]\displaystyle{ [a, b] }[/math] и дифференцируемая на интервале [math]\displaystyle{ (a, b) }[/math], принимает на концах отрезка [math]\displaystyle{ [a,b] }[/math] одинаковые значения, то на интервале [math]\displaystyle{ (a, b) }[/math] найдётся хотя бы одна точка, в которой производная функции равна нулю. |
Доказательство

Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма производная в этой точке равна 0.
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Следствия
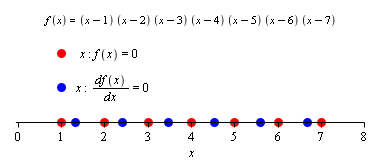
Если дифференцируемая функция обращается в ноль в [math]\displaystyle{ n }[/math] различных точках, то её производная обращается в ноль по крайней мере в [math]\displaystyle{ n-1 }[/math] различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
Если все корни многочлена n-ой степени действительные, то и корни всех его производных до [math]\displaystyle{ n-1 }[/math] включительно — также исключительно действительные.
Дифференцируемая функция на отрезке между двумя своими точками имеет касательную, параллельную секущей/хорде, проведённой через эти две точки.
См. также
Примечания
- ↑ Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. — Численные методы, стр.43
Литература
- Фихтенгольц Г. М. Основы математического анализа. — М.: «Наука», 1962. — Т. 1. — С. 225. — 607 с.