Грасгоф, Франц

В Руниверсалис есть статьи о других людях с фамилией Грасгоф.

Франц Грасгоф
нем. Franz Grashof
Место рождения	Дюссельдорф, Германия
Место смерти	Карлсруэ, Германия
Научная сфера	механика, машиностроение

Гра́сгоф, Франц (нем. Franz Grashof; 11 июля 1826, Дюссельдорф — 26 октября 1893, Карлсруэ) — немецкий механик и машиностроитель.

Биография

Детство и юность

Франц Грасгоф родился 11 июля 1826 года в семье Елизаветы Софии Доротеи Флорентины Брюггеман (нем. Lisette Sophie Dorothea Florentine Bruggemann) и Карла Грасгофа (нем. Karl Grashof), преподавателя классической филологии в Дюссельдорфской Королевской гимназии. Его дядей был придворный художник Отто Грасгоф. Несмотря на гуманитарное окружение в семье, Франц рано проявил интерес к технике; уже с 15 лет он работал слесарем, посещая после работы ремесленное училище.

В октябре 1844 года Франц Грасгоф поступил в Берлинский Королевский коммерческий институт, где изучал математику, физику и машиностроение. Однако в 1847 году Грасгоф, прервав обучение, пошёл на военную службу: год он прослужил добровольцем в стрелковом батальоне, а в 1848—1851 годах служил на флоте матросом и совершил на парусном судне плавания в Нидерландскую Ост-Индию и Австралию. После этого он разочаровался в избранной им было карьере морского офицера (не последнюю роль сыграла близорукость, которой он страдал) и вернулся в Берлин, где с 1852 года продолжал обучение в Королевском коммерческом институте.

Профессиональная карьера

В 1854 году Грасгоф окончил Берлинский Королевский коммерческий институт и остался работать в нём, преподавая математику и механику. В 1856 году группа из 23 молодых инженеров, в которую входил и Грасгоф, основали существующее и поныне Общество немецких инженеров (нем. Verein Deutscher Ingenieure). Грасгоф стал редактором журнала «Zeitschrift des VDI», учреждённого этим обществом и издававшегося начиная с 1 января 1857 года; в нём учёный опубликовал и ряд своих статей по различным вопросам прикладной механики. В 1860 году Ростокский университет присвоил Францу Грасгофу звание почётного доктора.

Памятник Францу Грасгофу в Карлсруэ

В 1863 году после смерти Фердинанда Редтенбахера Грасгоф стал его преемником на посту профессора кафедры прикладной механики и теории машин Политехникума Карлсруэ. Здесь он читал лекции по сопротивлению материалов, гидравлике, термодинамике и конструированию машин, причём — по общему мнению — его лекции отличались точностью и ясностью языка.

В 1883 году Грасгоф перенёс инсульт, последствия которого существенно ограничили его творческую активность. В 1891 году последовал новый инсульт, от которого учёный так и не оправился.

Умер 26 октября 1893 года в Карлсруэ.

Научная деятельность

Работы Грасгофа по кинематике

Основное направление исследований Грасгофа — прикладная механика (в частности, кинематика механизмов). Был сторонником аналитических методов в механике. Из результатов, полученных Грасгофом, в современных учебниках теоретической механики обычно приводится теорема Грасгофа о проекциях скоростей (не всегда — с упоминанием имени автора).

Теорема Грасгофа о проекциях скоростей

Рассмотрим две точки — [math]\displaystyle{ A^* }[/math] и [math]\displaystyle{ B^* }[/math] — некоторой механической системы, и пусть [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math] — их текущие положения. Теорема Грасгофа о проекциях скоростей в общем случае формулируется следующим образом: «Если на точки [math]\displaystyle{ A^* }[/math] и [math]\displaystyle{ B^* }[/math] наложена жёсткая связь, то проекции их скоростей на прямую, соединяющую текущие положения этих точек, равны»:

[math]\displaystyle{ \mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{\!A}}\;=\;\mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{B}} }[/math] .

Обычно данную теорему применяют к точкам абсолютно твёрдого тела, и в этом случае её формулируют так: «Проекции скоростей двух произвольных точек твёрдого тела на прямую, соединяющую эти точки, равны между собой».

Приведём доказательство этой теоремы. Достаточно показать, что

[math]\displaystyle{ \mathrm{pr}_{_{AB}}\,(\mathbf{v}_{_{B}}-\mathbf{v}_{_{\!A}})\;\equiv\;\mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{\!AB}}\;=\;0 }[/math]

(здесь [math]\displaystyle{ \mathbf{v}_{_{\!AB}} }[/math] — скорость точки [math]\displaystyle{ B^* }[/math] относительно точки [math]\displaystyle{ A^* }[/math]).

Дифференцируя по времени [math]\displaystyle{ t }[/math] условие жёсткой связи

[math]\displaystyle{ (\,\mathbf{r}_{_{\!AB}},\,\mathbf{r}_{_{\!AB}})\;=\;\mathrm{const} }[/math]

(представленное в виде условия постоянства скалярного квадрата радиус-вектора точки [math]\displaystyle{ B }[/math] относительно точки [math]\displaystyle{ A }[/math]), получаем:

[math]\displaystyle{ \left(\,{\mathrm{d}\over \mathrm{d}t}\,\mathbf{r}_{_{\!AB}},\,\mathbf{r}_{_{\!AB}}\right)\,+\,\left(\,\mathbf{r}_{_{\!AB}},\,{\mathrm{d}\over \mathrm{d}t}\,\mathbf{r}_{_{\!AB}}\right)\;\equiv\;2\,(\,\mathbf{r}_{_{\!AB}},\,\mathbf{v}_{_{\!AB}})\;=\;0 }[/math] .

Итак, [math]\displaystyle{ (\,\mathbf{r}_{_{\!AB}},\,\mathbf{v}_{_{\!AB}})\;=\;0 }[/math] , то есть [math]\displaystyle{ \mathbf{v}_{_{\!AB}} \perp \mathbf{r}_{_{\!AB}} }[/math] .

Пусть теперь [math]\displaystyle{ \mathbf{e}\,=\,\mathbf{r}_{_{\!AB}}/\left|\mathbf{r}_{_{\!AB}}\right| }[/math] — единичный вектор оси [math]\displaystyle{ AB }[/math]. Имеем:

[math]\displaystyle{ \mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{\!AB}}\;=\;(\,\mathbf{e},\,\mathbf{v}_{_{\!AB}})\;=\;{1 \over \left|\mathbf{r}_{_{\!AB}}\right|}\,(\,\mathbf{r}_{_{\!AB}},\,\mathbf{v}_{_{\!AB}})\;=\;0 }[/math] .

Теорема доказана.

Скорости двух точек абсолютно твёрдого тела

[math]\displaystyle{ A }[/math]

[math]\displaystyle{ \alpha }[/math]

[math]\displaystyle{ V_{A} }[/math]

[math]\displaystyle{ B }[/math]

[math]\displaystyle{ \beta }[/math]

[math]\displaystyle{ V_{B} }[/math]

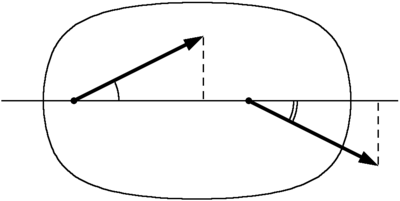
Теорема Грасгофа о проекциях скоростей нередко оказывается полезной при решении конкретных задач кинематики абсолютно твёрдого тела. Вот — типичный пример.

Пусть [math]\displaystyle{ A^* }[/math] и [math]\displaystyle{ B^* }[/math] — точки абсолютно твёрдого тела, [math]\displaystyle{ \alpha }[/math] и [math]\displaystyle{ \beta }[/math] — углы векторов [math]\displaystyle{ \mathbf{v}_{_{\!A}} }[/math] и [math]\displaystyle{ \mathbf{v}_{_{B}} }[/math] с прямой [math]\displaystyle{ AB }[/math]. Найти [math]\displaystyle{ V_{B} }[/math], если известны [math]\displaystyle{ V_{A} }[/math], [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ \beta }[/math] (жирный шрифт при наборе [math]\displaystyle{ V_{B} }[/math] не использовался, так что речь идёт о нахождении модуля вектора скорости точки [math]\displaystyle{ B^* }[/math]).

Имеем:

[math]\displaystyle{ \mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{\!A}}\;=\;\mathrm{pr}_{_{AB}}\,\mathbf{v}_{_{B}} }[/math] ,

то есть

[math]\displaystyle{ V_{A}\,\cos\,\alpha\;=\;V_{B}\,\cos\,\beta }[/math] ;

отсюда

[math]\displaystyle{ V_{B}\;=\;V_{A}\,{{\cos\,\alpha} \over {\cos\,\beta}} }[/math] .

Решение задачи найдено. Подчеркнём ещё раз, что мы нашли только модуль вектора [math]\displaystyle{ \mathbf{v}_{_{B}} }[/math]. Полностью найти вектор [math]\displaystyle{ \mathbf{v}_{_{B}} }[/math], пользуясь только теоремой Грасгофа, мы бы не смогли.

Так обстоят дела и в общем случае. Теорема Грасгофа о проекциях скоростей сама по себе не позволяет решать задачи кинематики до конца: всегда требуется какая-либо дополнительная информация.

Работы Грасгофа по сопротивлению материалов

Грасгоф проявлял большой интерес к сопротивлению материалов и в 1866 году выпустил руководство по данному предмету, переизданное в расширенном виде в 1878 году под названием «Теория упругости и прочности» (нем. Theorie der Elasticität und Festigkeit). Книга стала первой попыткой ввести элементы теории упругости в ориентированный на инженеров курс сопротивления материалов. Причём Грасгоф не ограничивается изложением лишь элементарного сопротивления материалов, но также вводит основные уравнения теории упругости, которыми пользуется при изложении теории изгиба и кручения призматических стержней и теории пластин. В задаче об изгибе стержня Грасгоф находит решения для некоторых форм поперечного сечения, не рассматривавшихся Сен-Венаном. Он продолжает исследования Вейсбаха по изучению сложного напряжённого состояния. В ряде разделов курса Грасгоф находит новые, оригинальные результаты.

Работы Грасгофа по машиноведению

Грасгоф работал также в области машиноведения. Его главный труд — «Теоретическое машиностроение» (тт. 1—3, 1875—1890 гг.), в котором он развил учение Ф. Рёло о кинематических парах и кинематических цепях.

В данном труде Грасгоф рассматривал движение как плоских, так и пространственных механизмов. Анализируя общий случай движения в пространстве, он указывал, что простая замкнутая цепь принуждённого движения с вращательными кинематическими парами должна состоять из семи звеньев, а также обсуждал возможности уменьшения числа звеньев при частных расположениях осей шарниров.

В учебниках по теории механизмов и машин часто приводится теорема Грасгофа о шарнирном четырёхзвеннике.

Теорема Грасгофа о шарнирном четырёхзвеннике

Данная теорема (иногда именуемая также правилом Грасгофа) устанавливает условие существования кривошипа в шарнирном четырёхзвеннике. Речь идёт о плоском механизме из трёх подвижных звеньев (то есть твёрдых тел, образующих механизм) 1, 2, 3 и стойки (неподвижного звена) 0, у которого все звенья соединены между собой вращательными кинематическими парами.

Шарнирный четырёхзвенник

[math]\displaystyle{ y }[/math]

[math]\displaystyle{ O }[/math]

[math]\displaystyle{ \mathit{1} }[/math]

[math]\displaystyle{ A }[/math]

[math]\displaystyle{ \mathit{2} }[/math]

[math]\displaystyle{ B }[/math]

[math]\displaystyle{ \mathit{3} }[/math]

[math]\displaystyle{ C }[/math]

[math]\displaystyle{ x }[/math]

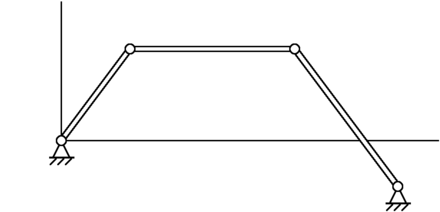
Для звеньев плоских механизмов в теории механизмов и машин используют следующую терминологию:

• кривошип — звено плоского механизма, которое образует вращательную пару со стойкой и может совершать вокруг оси пары полный оборот;
• коромысло — звено плоского механизма, которое образует вращательную пару со стойкой, но не может совершать полный оборот вокруг оси пары;
• шатун — звено плоского механизма, связанное вращательными парами с подвижными его звеньями, но не со стойкой.

Теорема Грасгофа о шарнирном четырёхзвеннике формулируется так: "Наименьшее звено является кривошипом, если сумма длин наименьшего и любого другого звена меньше суммы длин остальных двух звеньев (под «наименьшим» понимается звено минимальной длины).

Поясним данную формулировку. Пусть [math]\displaystyle{ a }[/math] — длина самого короткого звена (для механизма, изображённого на рисунке, [math]\displaystyle{ a=\left|OA\right| }[/math]), [math]\displaystyle{ d }[/math] — длина одного из соединённых с ним звеньев, [math]\displaystyle{ b }[/math] и [math]\displaystyle{ c }[/math] — длины остальных звеньев механизма.

Предположим сначала, что [math]\displaystyle{ d\,\gt \,b }[/math] и [math]\displaystyle{ d\,\gt \,c }[/math] (на рисунке, где [math]\displaystyle{ b=\left|AB\right| }[/math], [math]\displaystyle{ c=\left|BC\right| }[/math], [math]\displaystyle{ d=\left|OC\right| }[/math], это именно так). Элементарный геометрический анализ показывает, что условием полной проворачиваемости звена наименьшей длины относительно звена длины [math]\displaystyle{ d }[/math]  является выполнение неравенства

[math]\displaystyle{ a\,+\,d\;\lt \;b\,+\,c }[/math] .

Если же [math]\displaystyle{ d\,\lt \,b }[/math] или [math]\displaystyle{ d\,\lt \,c }[/math], то данное неравенство тем более будет выполняться. Из этих рассмотрений и следует справедливость теоремы Грасгофа в приведённой выше формулировке (рассмотрение предельного случая, когда неравенство обращается в равенство, мы опускаем).

Применяя правило Грасгофа, удаётся подразделить все шарнирные четырёхзвенники на 3 группы:

• механизм будет кривошипно-коромысловым, если длины его звеньев удовлетворяют правилу Грасгофа и за стойку принято звено, соседнее с наименьшим;
• механизм будет двухкривошипным, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, и за стойку принято самое короткое звено;
• механизм будет двухкоромысловым, если либо правило Грасгофа не выполнено, либо оно выполнено, но самое короткое звено не соединено со стойкой (то есть оно является шатуном и потому не может быть кривошипом).

Так, изображённый на рисунке шарнирный четырёхзвенник является двухкоромысловым механизмом, поскольку правило Грасгофа для него не выполняется.

Работы Грасгофа по теории теплопередачи

Грасгоф работал также в области гидравлики и теплотехники, где изучал, в частности, процессы конвекции. В теории теплопередачи известно названное в его честь число Грасгофа — критерий подобия, определяющий процесс теплообмена при свободном движении в поле гравитации и являющийся мерой соотношения архимедовой (подъёмной) силы, вызванной неравномерным распределением плотности в неоднородном поле температур, и сил межмолекулярного трения.

Семья

В 1854 году Франц Грасгоф женился на Генриетте Ноттебом (нем. Henriette Nottebohm), дочери землевладельца. У них родились сын и две дочери; одна из дочерей, Елизавета, позднее вышла замуж за известного архитектора и скульптора Карла Хоффаккера (нем. Karl Hoffacker).

Память

Табличка с названием улицы Грасгофа в Карлсруэ

В 1894 году Общество немецких инженеров учредило в честь Франца Грасгофа (в 1856—1890 годах — первый директор общества) свою высшую награду — памятную медаль Грасгофа, которая вручается в качестве премии для инженеров, имеющих выдающиеся научные или профессиональные заслуги в области техники.

В 1986 году в Карлсруэ был воздвигнут памятник Францу Грасгофу. В честь него названы улицы в Бремене, Дюссельдорфе, Карлсруэ и Мангейме.

Публикации

• Grashof, Franz.  Die Festigkeitslehre mit besonderer Rücksicht auf die Bedürfnisse des Maschinenbauses: Abriss von Vorträgen an der Polytechnischen Schule zu Carlsruhe. — Berlin: R. Gaertner, 1866. — xiv + 293 S.
• Grashof, Franz.  Theorie der Elasticität und Festigkeit: mit Bezug auf ihre Anwendungen in der Technik. — Berlin: R. Gaertner, 1878. — viii + 408 S.
• Grashof, Franz.  Theoretische Maschinenlehre. Bd. 1. Hydraulik nebst mechanischer Wärmetheorie und allgemeiner Theorie der Heizung. — Leipzig: L. Voss, 1875. — xiv + 972 S.
• Grashof, Franz.  Theoretische Maschinenlehre. Bd. 2. Theorie der getriebe und der mechanischen Messinstrumente. — Leipzig: L. Voss, 1883. — xii + 873 S.
• Grashof, Franz.  Theoretische Maschinenlehre. Bd. 3. Theorie der Kraftmaschinen. — Leipzig: L. Voss, 1890. — xii + 891 S.

Литература

• Артоболевский И. И.  Теория механизмов. — М.: Наука, 1965. — 776 с.
• Боголюбов А. Н.  Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
• Кафаров В. В.  Основы массопередачи. — М.: Высшая школа, 1972. — 496 с.
• Павловский М. А., Акинфиева Л. Ю., Бойчук О. Ф.  Теоретическая механика. Статика. Кинематика. — Киев: Вища школа, 1989. — 351 с. — ISBN 5-11-001177-X.
• Тимошенко С. П.  История науки о сопротивлении материалов с краткими сведениями из истории теории упругости и теории сооружений / Пер. с англ. под ред. А. Н. Митинского. — М.: ГИТТЛ, 1957. — 536 с.
• Фролов К. В., Попов С. А., Мусатов А. К.  Теория механизмов и машин / Под ред. К. В. Фролова. — М.: Высшая школа, 1987. — 496 с.
• Юдин В. А., Петрокас Л. В.  Теория механизмов и машин. — М.: Высшая школа, 1967. — 528 с.