Сумма Минковского
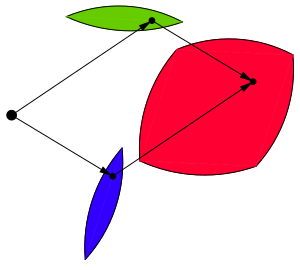
Суммой Минковского двух подмножеств A и B линейного пространства V (или произвольной группы) называется множество C, состоящее из сумм всевозможных векторов из A и B:
- [math]\displaystyle{ C = \left\{\,c \mid c=a+b, a\in A, b\in B\,\right\} }[/math]
Аналогично определяется произведение множества на число:
- [math]\displaystyle{ \lambda A = \left\{\,\lambda a \mid a\in A\,\right\} }[/math]
Свойства
- Если множество A выпукло, то
- [math]\displaystyle{ (\lambda + \mu) A = \lambda A + \mu A }[/math]
- для любых [math]\displaystyle{ \lambda \gt 0 }[/math] и [math]\displaystyle{ \mu \gt 0 }[/math].
- [math]\displaystyle{ \lambda (A+B)= \lambda A + \lambda B }[/math]
- [math]\displaystyle{ A + B = B + A }[/math]
- [math]\displaystyle{ A + \left\{0\right\} = A }[/math]
О разности Минковского
Множества с введенной на них суммой Минковского не образуют линейного пространства (даже выпуклые). Это связано с отсутствием обратного элемента (элемент -A, очевидно, таковым не является).
- Разностью Минковского множеств A и B называется максимальное множество C такое, что
- [math]\displaystyle{ C + B \subset A }[/math],
- но легко видеть, что для многих множеств (например, квадрата и круга) разность Минковского не является операцией, обратной к сумме.
- Альтернативно можно продолжить сумму Минковского на линейное пространство пар выпуклых множеств (A,B) с отношением эквивалентности
- [math]\displaystyle{ (A, B) \sim (C, D) \Leftrightarrow A + D = B + C }[/math]
Разность Минковского также называют геометрической разностью множеств.
Вариации и обобщения
- Множество сумм — аналогичное определение для подмножеств групп в аддитивной и арифметической комбинаторике. Наравне с суммами рассматривается произведения множеств [math]\displaystyle{ A \times B = \left\lbrace{ab : a \in A, b \in B}\right\rbrace }[/math] и другие операции.
Литература
- Половинкин Е. С., Балашов М. В. Элементы выпуклого и сильно выпуклого анализа. — М.: ФИЗМАТЛИТ, 2004. — 416 с. — ISBN 5-9221-0499-3.