Регистр сдвига с обратной связью по переносу
Регистр сдвига с обратной связью по переносу (англ. feedback with carry shift register, FCSR) — сдвиговый[англ.] регистр битовых слов, арифметический аналог регистра сдвига с линейной обратной связью, отличается от него наличием регистра переноса. Применяется для генерации псевдослучайных последовательностей битов, а также использовался для создания потокового шифра F-FCSR.
История
В 1994 регистр сдвига с обратной связью по переносу был изобретен Горески (англ. Goresky) и Клаппером (англ. Klapper), а также независимо от них Марсаглией (англ. Marsaglia) и Заманом (англ. Zaman), Кутюром (англ. Couture) и Л’Экуером (англ. L’Ecuyer). Причем Клаппер и Горески хотели использовать его для криптоанализа суммирующего генератора. С другой стороны, Марсаглия, Заман, Кутюр, Л’Экуер были нацелены найти хороший генератор случайных чисел для решения таких задач, как использование квази-Монте-Карло метода.[1]
Описание

В FCSR есть сдвиговый регистр, функция обратной связи и регистр переноса. Длина сдвигового регистра — количество битов. Когда нужно извлечь бит, все биты сдвигового регистра сдвигаются вправо на одну позицию.[2]
Вместо выполнения операции XOR над всеми битами отводной последовательности эти биты складываются друг с другом и с содержимым регистра переноса. Результат [math]\displaystyle{ mod }[/math] [math]\displaystyle{ 2 }[/math] и становится новым битом. Результат, деленный на [math]\displaystyle{ 2 }[/math], становится новым содержимым регистра переноса.[3]
[math]\displaystyle{ m }[/math] — значение регистра переноса
- [math]\displaystyle{ \sigma={q_1}{a_{k-1}}+\cdots+{q_k}{a_0}+m }[/math]
- [math]\displaystyle{ {a_k}={\sigma} {mod}{2} }[/math]
- [math]\displaystyle{ {m^\prime}=[{\sigma}/2] }[/math]
[math]\displaystyle{ ({a_k},\cdots, {a_1}) }[/math] — новое состояние регистра
[math]\displaystyle{ m^\prime }[/math] — новое значение регистра переноса
Пример

Рассмотрим пример 3-битового регистра с ответвлениями в первой и второй позициях. Пусть его начальное значение [math]\displaystyle{ \left[0,\;0,\;1\right] }[/math], а начальное содержимое регистра переноса равно [math]\displaystyle{ [0] }[/math]. Выходом будет являться крайний правый бит сдвигового регистра. Дальнейшие состояния регистра приведены в таблице ниже:
| Номер шага | Сдвиговый регистр | Регистр переноса |
|---|---|---|
| 0 | [math]\displaystyle{ \left[0,\;0,\;1\right] }[/math] | 0 |
| 1 | [math]\displaystyle{ \left[1,\;0,\;0\right] }[/math] | 0 |
| 2 | [math]\displaystyle{ \left[0,\;1,\;0\right] }[/math] | 0 |
| 3 | [math]\displaystyle{ \left[1,\;0,\;1\right] }[/math] | 0 |
| 4 | [math]\displaystyle{ \left[1,\;1,\;0\right] }[/math] | 0 |
| 5 | [math]\displaystyle{ \left[1,\;1,\;1\right] }[/math] | 0 |
| 6 | [math]\displaystyle{ \left[0,\;1,\;1\right] }[/math] | 1 |
| 7 | [math]\displaystyle{ \left[1,\;0,\;1\right] }[/math] | 1 |
| 8 | [math]\displaystyle{ \left[0,\;1,\;0\right] }[/math] | 1 |
| 9 | [math]\displaystyle{ \left[0,\;0,\;1\right] }[/math] | 1 |
| 10 | [math]\displaystyle{ \left[0,\;0,\;0\right] }[/math] | 1 |
| 11 | [math]\displaystyle{ \left[1,\;0,\;0\right] }[/math] | 0 |
Конечное внутреннее состояние (включая содержимое регистра переноса) совпадает со вторым внутренним состоянием. С этого момента последовательность циклически повторяется с периодом равным [math]\displaystyle{ 10 }[/math]. Стоит также упомянуть, что регистр переноса является не битом, а числом. Его размер должен быть не меньше [math]\displaystyle{ \log_2 t }[/math], где [math]\displaystyle{ t }[/math] — число ответвлений. В примере только три ответвления, поэтому регистр переноса однобитовый. Если бы было четыре ответвления, то регистр переноса состоял бы из двух битов и мог принимать значения [math]\displaystyle{ 0, 1, 2 }[/math] или [math]\displaystyle{ 3 }[/math].[3]
Свойства
В отличие от LFSR, для FCSR существует задержка, прежде чем он перейдёт в циклический режим, то есть начнёт генерировать циклически повторяемую последовательность. В зависимости от выбранного начального состояния возможны 4 различных случая:[3]
- Начальное состояние может оказаться частью максимального периода.
- Начальное состояние может перейти в последовательность максимального периода, после некоторой начальной задержки.
- Начальное состояние может после начальной задержки породить последовательность нулей.
- Начальное состояние может после начальной задержки породить последовательность единиц.
Опытным путём можно проверить, чем закончится конкретное начальное состояние. Нужно запустить FCSR на некоторое время. (Если [math]\displaystyle{ m }[/math] — начальный объем памяти, а [math]\displaystyle{ t }[/math] — количество ответвлений, то достаточно [math]\displaystyle{ {~\log_2 t}+{~\log_2 m}+1 }[/math] тактов.) Если выходной поток вырождается в бесконечную последовательность нулей и единиц за [math]\displaystyle{ n }[/math] бит, где [math]\displaystyle{ n }[/math] — длина FCSR, то не стоит использовать это начальное состояние. [3]
Также, стоит отметить, что ряд ключей генератора на базе FCSR будут слабыми, так как начальное состояние FCSR соответствует ключу потокового шифра. [3]
Максимальный период FCSR равен [math]\displaystyle{ q-1 }[/math] , где [math]\displaystyle{ q }[/math] — целое число связи. Это число задает ответвления и определяется как:
[math]\displaystyle{ q={2q_1}+{{2^2}q_2}+{{2^3}q_3}+\cdots+{{2^n}q_n}-1 }[/math]
[math]\displaystyle{ q }[/math] — должно быть простым числом, для которого 2 является примитивным корнем.[3][1]
Связь с LFSR
Также, как анализ LFSR основан на сложении примитивных многочленов mod 2, анализ FCSR основан на сложении чисел, называемых 2-adic. В мире 2-adic чисел существуют аналоги для всего. Точно также, как определяется линейная сложность, можно определить 2-adic сложность. Существует 2-adic аналог и для алгоритма Берлекэмпа-Мэсси. Это означает, что число возможных потоковых шифров по крайней мере удвоилось. Все что можно делать с LFSR, можно делать и с FCSR.[3]
Варианты реализации
Конфигурация Галуа

Конфигурация Галуа состоит из:
- n — битного главного регистра [math]\displaystyle{ M=(m_0,\cdots,{m_{n-1}}) }[/math] , с некоторыми фиксированными ответвлениями [math]\displaystyle{ d_0, \cdots, d_{n-1} }[/math]
- n-1 — битного регистра переноса [math]\displaystyle{ C=(c_0,\cdots,c_{n-2}) }[/math]
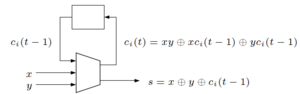
В момент времени t состояние [math]\displaystyle{ (M,C) }[/math] изменяется следующим образом:
1. [math]\displaystyle{ x_i=m_{i+1} + {c_i}{d_i} + {m_0}{d_i} }[/math] , для всех [math]\displaystyle{ 0 \leq i \lt n }[/math] , с [math]\displaystyle{ m_{n}=0 }[/math] и [math]\displaystyle{ c_{n-1}=0 }[/math] и где [math]\displaystyle{ m_0 }[/math] представляет бит обратной связи.
2. обновляется состояние: [math]\displaystyle{ m_i \leftarrow {x_i}mod2 }[/math] , для всех [math]\displaystyle{ i \in [0 \dots n-1] }[/math] и [math]\displaystyle{ c_i \leftarrow {x_i}div2 }[/math] , для всех [math]\displaystyle{ i \in [0 \dots n-2] }[/math] .[4][5]
Конфигурация Фибоначчи

Конфигурация Фибоначчи состоит из:
- n — битного главного регистра [math]\displaystyle{ M=(m_0,\cdots,{m_{n-1}}) }[/math]
- ответвления [math]\displaystyle{ (d_0, \cdots, d_{n-1}) }[/math] связаны с регистром переноса [math]\displaystyle{ c }[/math] , состоящего из [math]\displaystyle{ w_H(d) }[/math] битов, где [math]\displaystyle{ w_H(d) }[/math] вес Хамминга для [math]\displaystyle{ d=(1+|q|)/2 }[/math]
Состояние [math]\displaystyle{ (M,c) }[/math] изменяется следующим образом:
1. [math]\displaystyle{ x = c+ \sum^{n-1}_{i=0} {{m_i}{d_{n-1-i}}} }[/math] ;
2. обновляем состояние: [math]\displaystyle{ M \leftarrow (m_1, \dots , m_{n-1}, x mod2) }[/math] , [math]\displaystyle{ c \leftarrow x div2 }[/math] .[4][5]
Возможные варианты использования в генераторах
Чередующиеся генераторы «стоп-пошел»
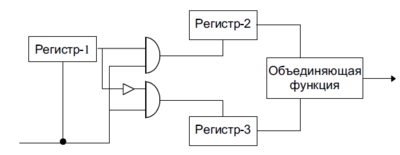
Основная статья: Генератор «стоп-пошел»
В нём используются три регистра сдвига различной длины. Здесь Регистр-1 управляет тактовой частотой 2-го и 3-го регистров, то есть Регистр-2 меняет своё состояние, когда выход Регистра-1 равен единице, а Регистр-3 — когда выход Регстра-1 равен нулю.[3]
Эти регистры используют FCSR вместо некоторых LFSR, и операция XOR может быть заменена сложением с переносом.
- Генератор «стоп-пошел» FCSR : Регистр-1, Регистр-2, Регистр-3 — это FCSR. Объединяющая функция — XOR.
- Генератор «стоп-пошел» FCSR/LFSR : Регистр-1 — FCSR; Регистр-2, Регистр-3 — LFSR. Объединяющая функция — сложение с переносом.
- Генератор «стоп-пошел» FCSR/LFSR : Регистр-1 — LFSR; Регистр-2, Регистр-3 — FCSR. Объединяющая функция — XOR.[3]
Каскадные генераторы
Основная статья: Каскад Голлманна
Данная схема представляет собой улучшенную версию генератора «стоп-пошёл». Он состоит из последовательности регистров, тактирование каждого из которых управляется предыдущим регистром. Если выходом Регистра-1 в момент времени является 1,то тактируется Регистр-2. Если выходом Регистра-2 в момент времени является 1, то тактируется Регистр-3, и так далее. Выход последнего регистра является выходом генератора.[3]
Существует два способа использовать FCSR в каскадных генераторах:
- Каскад FCSR. Каскад Голлманна с FCSR вместо LFSR.
- Каскад FCSR/LFSR. Каскад Голлманна с генераторами, меняющими LFSR на FCSR и наоборот.[3]
Комбинированные генераторы

Эти генераторы используют переменное количество FCSR и/или LFSR и множество функций, объединяющих регистры. Операция XOR разрушает алгебраические свойства FCSR, поэтому имеет смысл использовать эту операцию для их объединения.[3]
- Генератор четности FCSR. Все регистры — FCSR, а объединяющая функция — XOR.
- Генератор четности LFSR/FCSR. Используется смесь LFSR и FCSR, а объединяющая функция — XOR.
- Пороговый генератор FCSR. Все регистры — FCSR, а объединяющая функция — мажорирование.
- Пороговый генератор LFSR/FCSR. Используется смесь LFSR и FCSR, а объединяющая функция — мажорирование.
- Суммирующий генератор FCSR. Все регистры — FCSR, а объединяющая функция — сложение с переносом.
- Суммирующий генератор LFSR/FCSR. Используется смесь LFSR и FCSR, а объединяющая функция — сложение с переносом.[3]
Применение
Регистры сдвига с обратной связью по переносу могут служить основой при создании различных генераторов (некоторые из них описывались выше), а также различных потоковых шифров.
F-FCSR
Основная статья : F-FCSR .
F-FCSR — семейство поточных шифров, основанное на использовании регистра сдвига с обратной связью по переносу(FCSR) с линейным фильтром на выходе. Идея шифра была предложена Терри Бергером, Франсуа Арно и Седриком Лараду. F-FCSR был представлен на конкурсе eSTREAM, был включен в список победителей конкурса в апреле 2008, но в дальнейшем была выявлена криптографическая слабость и в сентябре 2008 F-FCSR был исключен из списка eSTREAM.
См. также
Примечания
- ↑ 1,0 1,1 A. Klapper A Survey of Feedback with Carry Shift Registers (недоступная ссылка)
- ↑ A. Klapper and M. Goresky, Feedback Shift Registers, 2-Adic Span, and Combiners With Memory, in Journal of Cryptology vol. 10, pp. 111—147, 1997, [1] (недоступная ссылка)
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 Б. Шнайер, 2013.
- ↑ 4,0 4,1 A. Klapper and M. Goresky, Fibonacci and Galois Representations of Feedback with Carry Shift Registers, 2004, [2] Архивная копия от 23 сентября 2015 на Wayback Machine
- ↑ 5,0 5,1 Francois Arnault, Thierry Berger, C´edric Lauradoux, Marine Minier and Benjamin Pousse, A new approach for FCSRs, [3] Архивная копия от 2 июня 2018 на Wayback Machine
Литература
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. — Триумф, 2013. — 816 с. — ISBN 978-5-89392-527-2.


