Лемма Йонеды

Лемма Йонеды — результат о функторе Hom; теоретико-категорное обобщение классической теорико-групповой теоремы Кэли (если рассматривать группу как категорию из одного объекта). Лемма позволяет рассмотреть вложение произвольной категории в категорию функторов из неё в категорию множеств. Является важным инструментом, позволившим получить множество результатов в алгебраической геометрии и теории представлений.

Общий случай

В произвольной (локально малой) категории для данного объекта [math]\displaystyle{ A }[/math] можно рассмотреть ковариантный функтор Hom, обозначаемый:

[math]\displaystyle{ h^A = \mathrm{Hom}(A, -) }[/math].

Лемма Йонеды утверждает, что для любого объекта [math]\displaystyle{ A }[/math] категории [math]\displaystyle{ \mathcal C }[/math], естественные преобразования из [math]\displaystyle{ h^A }[/math] в произвольный функтор [math]\displaystyle{ F }[/math] из категории [math]\displaystyle{ \mathcal C }[/math] в категорию множеств [math]\displaystyle{ \mathbf{Set} }[/math] находятся во взаимно-однозначном соответствии с элементами [math]\displaystyle{ F(A) }[/math]:

[math]\displaystyle{ \mathrm{Nat}(h^A,F) \cong F(A) }[/math].

Для данного естественного преобразования [math]\displaystyle{ \Phi }[/math] из [math]\displaystyle{ h^A }[/math] в [math]\displaystyle{ F }[/math] соответствующий элемент [math]\displaystyle{ F(A) }[/math] — это [math]\displaystyle{ u = \Phi_A(\mathrm{id}_A) }[/math], то есть естественное преобразование однозначно определяется образом тождественного морфизма.

Контравариантная версия леммы рассматривает контравариантный функтор:

[math]\displaystyle{ h_A = \mathrm{Hom}(-, A) }[/math],

отправляющий [math]\displaystyle{ X }[/math] во множество [math]\displaystyle{ \mathrm{Hom}(X, A) }[/math]. Для произвольного контравариантного функтора [math]\displaystyle{ G }[/math] из [math]\displaystyle{ \mathcal C }[/math] в [math]\displaystyle{ \mathbf{Set} }[/math]

[math]\displaystyle{ \mathrm{Nat}(h_A,G) \cong G(A) }[/math].

Используется мнемоническое правило «падать во что-то» при рассмотрении морфизмов в зафиксированный объект.

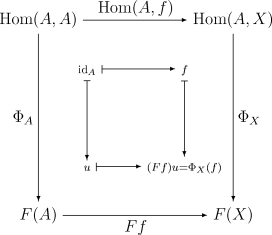
Доказательство леммы Йонеды представлено на следующей коммутативной диаграмме:

Диаграмма показывает, что естественное преобразование [math]\displaystyle{ \Phi }[/math] полностью определяется [math]\displaystyle{ \Phi_A(\mathrm{id}_A)=u }[/math], так как для любого морфизма [math]\displaystyle{ f \colon A \to X }[/math]:

[math]\displaystyle{ \Phi_X(f) = (Ff)u }[/math].

Более того, эта формула задаёт естественное преобразование для любого [math]\displaystyle{ u \in F(A) }[/math] (так как диаграмма коммутативна). Доказательство контравариантного случая аналогично.

Вложение Йонеды

Частный случай леммы Йонеды — когда функтор [math]\displaystyle{ F }[/math] также является функтором Hom. В этом случае ковариантная версия леммы Йонеды утверждает, что:

[math]\displaystyle{ \mathrm{Nat}(h^A,h^B) \cong \mathrm{Hom}(B,A) }[/math].

Отображение каждого объекта [math]\displaystyle{ A }[/math] категории [math]\displaystyle{ \mathcal C }[/math] в соответствующий Hom-функтор [math]\displaystyle{ h^A = Hom(A, -) }[/math] и каждый морфизм [math]\displaystyle{ f \colon B \to A }[/math] в соответствующее естественное преобразование [math]\displaystyle{ \mathrm{Hom}(f, -) }[/math] задаёт контравариантный функтор [math]\displaystyle{ h^{-} }[/math] из [math]\displaystyle{ \mathcal C }[/math] в [math]\displaystyle{ \mathbf{Set}^\mathcal C }[/math], либо ковариантный функтор:

[math]\displaystyle{ h^{-}\colon \mathcal C^{\text{op}} \to \mathbf{Set}^\mathcal C }[/math].

В этой ситуации лемма Йонеды утверждает, что [math]\displaystyle{ h^{-} }[/math] — вполне унивалентный функтор, то есть задаёт вложение [math]\displaystyle{ \mathcal C^{op} }[/math] в категорию функторов в [math]\displaystyle{ \mathbf{Set} }[/math].

В контравариантном случае по лемме Йонеды:

[math]\displaystyle{ \mathrm{Nat}(h_A,h_B) \cong \mathrm{Hom}(A,B) }[/math].

Следовательно [math]\displaystyle{ h_{-} }[/math] задаёт вполне унивалентный ковариантный функтор (вложение Йонеды):

[math]\displaystyle{ h_{-}\colon \mathcal C \to \mathbf{Set}^{\mathcal C^{\mathrm{op}}} }[/math].

Литература

• Freyd, Peter (1964), Abelian categories (2003 reprint ed.), Harper's Series in Modern Mathematics, Harper and Row, <http://www.tac.mta.ca/tac/reprints/articles/3/tr3abs.html> .
• Маклейн С. Глава 3. Универсальные конструкции и пределы // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 68—94. — 352 с. — ISBN 5-9221-0400-4.