Лексикографический поиск в ширину

Лексикографический поиск в ширину (англ. lexicographic breadth-first search, LBFS or Lex-BFS) — алгоритм упорядочивания вершин графа. Алгоритм отличается от алгоритма поиска в ширину и дает более упорядоченную^{[неизвестный термин]} последовательность вершин графа.

Алгоритм лексикографического поиска в ширину основан на идее разбиения на подмножества и впервые был разработан Роузом, Тарьяном и Люкером (1976). Более детальный обзор темы был представлен Корнейлом (2004). Лексикографический поиск в ширину используется как часть в других графических алгоритмах, например, распознавание хордальных графов, раскраска полностью расщепляемых графов.

Файл:LBFS 2.gif

Описание алгоритма

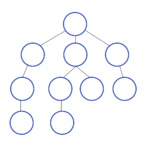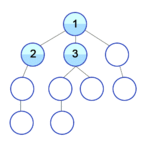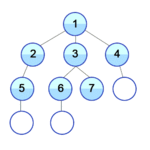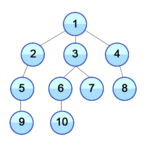
Для работы алгоритма необходимо задать вершину графа, с которой начинается обход. Описание алгоритма выглядит следующим образом:

• Инициализировать последовательность множеств вершин Σ состоящую из одного множества содержащего все вершины графа.
• Инициализировать пустую выходную последовательность вершин.
• Пока Σ непустое:
  • Из первого множества в Σ взять вершину v и удалить ее из множества.
  • Если первое множество в Σ стало пустым удалить его из Σ .
  • Добавить v в конец выходной последовательности вершин.
  • Для каждого ребра v-w:
    • Определить множество S в Σ которое содержит w.
    • Если множество S еще не разделялось при обработке v, создать новое пустое множество T и поместить его перед S в Σ.
    • Переместить вершину w из S в T и, если S стало пустым удалить его из Σ.

Каждая вершина обрабатывается один раз, каждое ребро тестируется только при обработке его двух вершин, и (в предположении, что обработка операций в последовательности множеств Σ занимает конечное время) каждая итерация внутреннего цикла занимает конечное время. Значит, также как и для алгоритмов поиска в глубину и поиска в ширину временная сложность алгоритма является линейной и составляет [math]\displaystyle{ O(\vert V \vert + \vert E \vert) }[/math].

Алгоритм называется лексикографическим поиском в ширину потому, что получаемый порядок похож на результат алгоритма поиска в ширину, но дополнительно строки и столбцы матрицы смежности сортируются в лексикографическом порядке.

Применение

Алгоритм лексикографического поиска в ширину используется для распознавания хордальных графов, раскраски вполне сепарабельных графов. Для распознавания единичных интервальных и интервальных графов используются многомаховые алгоритмы (алгоритм лексикографического поиска в ширину с вариациями применяется несколько раз).

Литература

• Brandstädt, Andreas; Le, Van Bang & Spinrad, Jeremy (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 0-89871-432-X .
• Bretscher, Anna; Corneil, Derek; Habib, Michel & Paul, Christophe (2008), A simple linear time LexBFS cograph recognition algorithm, SIAM Journal on Discrete Mathematics Т. 22 (4): 1277–1296, doi:10.1137/060664690, <http://www.liafa.jussieu.fr/~habib/Documents/cograph.ps> .
• Corneil, Derek G. (2004), Lexicographic breadth first search – a survey, Graph-Theoretic Methods in Computer Science: 30th International Workshop, WG 2004, Bad Honnef, Germany, June 21-23, 2004, Revised Papers, vol. 3353, Lecture Notes in Computer Science, Springer-Verlag, с. 1–19, DOI 10.1007/978-3-540-30559-0_1 .
• Habib, Michel; McConnell, Ross; Paul, Christophe & Viennot, Laurent (2000), Lex-BFS and partition refinement, with applications to transitive orientation, interval graph recognition and consecutive ones testing, Theoretical Computer Science Т. 234 (1–2): 59–84, doi:10.1016/S0304-3975(97)00241-7, <http://www.cecm.sfu.ca/~cchauve/MATH445/PROJECTS/MATH445-TCS-234-59.pdf>. Проверено 7 июня 2016.  Архивная копия от 26 июля 2011 на Wayback Machine.
• Rose, D. J.; Tarjan, R. E. & Lueker, G. S. (1976), Algorithmic aspects of vertex elimination on graphs, SIAM Journal on Computing Т. 5 (2): 266–283, DOI 10.1137/0205021 .