Измерительный мост
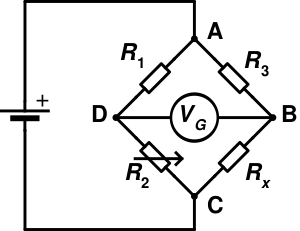

Измери́тельный мост (мост Уи́тстона, мо́стик Ви́тстона[1], англ. Wheatstone bridge) — электрическая схема или устройство для измерения электрического сопротивления. Предложен в 1833 году Самуэлем Хантером Кристи (англ. Samuel Hunter Christie) и в 1843 году усовершенствован Чарльзом Уитстоном[2]. Мост Уитстона относится к одинарным мостам в отличие от двойных мостов Томсона. Мост Уитстона — электрическое устройство, механическим аналогом которого являются аптекарские рычажные весы.
Измерение сопротивлений с помощью моста Уитстона
Принцип измерения сопротивления основан на уравнивании потенциала средних выводов двух ветвей (см. рисунок).
- В одну из ветвей включён двухполюсник (резистор), сопротивление которого требуется измерить ([math]\displaystyle{ R_x }[/math]).
Другая ветвь содержит элемент, сопротивление которого может регулироваться ([math]\displaystyle{ R_2 }[/math]; например, реостат).
Между ветвями (точками B и D; см. рисунок) находится индикатор. В качестве индикатора могут применяться:
- гальванометр;
- нуль-индикатор — прибор, отклонение стрелки которого показывает наличие тока в цепи и его направление, но не величину. На шкале такого прибора отмечено только одно число — ноль;
- вольтметр ([math]\displaystyle{ R_G }[/math] принимают равным бесконечности: [math]\displaystyle{ R_G = \infty }[/math]);
- амперметр ([math]\displaystyle{ R_G }[/math] принимают равным нулю: [math]\displaystyle{ R_G = 0 }[/math]).
Обычно в качестве индикатора используется гальванометр.
- Сопротивление [math]\displaystyle{ R_2 }[/math] второй ветви изменяют до тех пор, пока показания гальванометра не станут равны нулю, то есть потенциалы точек узлов D и B не станут равны. По отклонению стрелки гальванометра в ту или иную сторону можно судить о направлении протекания тока на диагонали моста BD (см. рисунок) и указывают в какую сторону изменять регулируемое сопротивление [math]\displaystyle{ R_2 }[/math] для достижения «баланса моста».
Когда гальванометр показывает ноль, говорят, что наступило «равновесие моста» или «мост сбалансирован». При этом:
- отношение [math]\displaystyle{ R_2 / R_1 }[/math] равно отношению [math]\displaystyle{ R_x / R_3 }[/math]:
- [math]\displaystyle{ \frac{ R_2 }{ R_1 } = \frac{ R_x }{ R_3 } , }[/math]
откуда
- [math]\displaystyle{ R_x = \frac{ R_2 R_3 }{ R_1 } ; }[/math]
- разность потенциалов между точками B и D (см. рисунок) равна нулю;
- ток по участку BD (через гальванометр) (см. рисунок) не протекает (равен нулю).
Сопротивления [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_3 }[/math] должны быть известны заранее.
- Изменяют сопротивление [math]\displaystyle{ R_2 }[/math] до баланса моста.
- Вычисляют искомое сопротивление [math]\displaystyle{ R_x }[/math]:
- [math]\displaystyle{ R_x = \frac{ R_2 R_3 }{ R_1 }. }[/math]
Вывод формулы см. ниже.
Точность
При плавном изменении сопротивления [math]\displaystyle{ R_2 }[/math] гальванометр способен зафиксировать момент наступления равновесия с большой точностью. Если величины [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_2 }[/math] и [math]\displaystyle{ R_3 }[/math] были измерены с малой погрешностью, величина [math]\displaystyle{ R_x }[/math] будет вычислена с большой точностью.
В процессе измерения сопротивление [math]\displaystyle{ R_x }[/math] не должно изменяться, так как даже небольшие его изменения приведут к нарушению баланса моста.
Недостатки
К недостаткам предложенного способа можно отнести:
- необходимость регулирования сопротивления [math]\displaystyle{ R_2 }[/math]. На поиски «равновесия» тратится время. Гораздо быстрее измерить несколько параметров цепи и вычислить [math]\displaystyle{ R_x }[/math] по другой формуле.
Условие баланса моста
Выведем формулу для расчёта сопротивления [math]\displaystyle{ R_x }[/math].

- Первый способ
Считается, что сопротивление гальванометра [math]\displaystyle{ R_G }[/math] мало настолько, что им можно пренебречь ([math]\displaystyle{ R_G = 0 }[/math]). То есть, можно вообразить, что точки B и D соединены (см. рисунок).
Воспользуемся правилами (законами) Кирхгофа. Выберем:
По первому правилу Кирхгофа сумма токов, входящих в точку (узел) равна нулю:
- для точки (узла) B:
- [math]\displaystyle{ I_3\ + I_G\ - I_x\ =\ 0 ; }[/math]
- для точки (узла) D:
- [math]\displaystyle{ I_1\ - I_2\ - I_G\ =\ 0 . }[/math]
По второму правилу Кирхгофа сумма напряжений в ветвях замкнутого контура равна сумме ЭДС в ветвях этого контура:
- для контура ABD:
- [math]\displaystyle{ ( R_3 \cdot I_3 )\ - ( R_G \cdot I_G )\ - ( R_1 \cdot I_1 ) = 0 ; }[/math]
- для контура BCD:
- [math]\displaystyle{ ( R_x \cdot I_x )\ - ( R_2 \cdot I_2 )\ + ( R_G \cdot I_G ) = 0 . }[/math]
Запишем 4‑е последних уравнения для «сбалансированного моста» (то есть учтём, что [math]\displaystyle{ I_G = 0 }[/math]):
- [math]\displaystyle{ \begin{cases} I_3 = I_x \\ I_1 = I_2 \\ R_3 \cdot I_3 = R_1 \cdot I_1 \\ R_x \cdot I_x = R_2 \cdot I_2 \end{cases} }[/math]
Поделив 4‑е уравнение на 3‑е, получим:
- [math]\displaystyle{ \frac{ R_x \cdot I_x }{ R_3 \cdot I_3 } = \frac{ R_2 \cdot I_2 }{ R_1 \cdot I_1 } . }[/math]
Выразив [math]\displaystyle{ R_x }[/math], получим:
- [math]\displaystyle{ R_x = \frac{ R_2 \cdot I_2 \cdot R_3 \cdot I_3 }{ I_1 \cdot R_1 \cdot I_x } . }[/math]
С учётом того, что
- [math]\displaystyle{ \begin{cases} I_3 = I_x \\ I_1 = I_2 \end{cases} }[/math]
получим
- [math]\displaystyle{ R_x = \frac{ R_2 \cdot R_3 }{ R_1 } . }[/math]
- Второй способ
Считается, что сопротивление гальванометра [math]\displaystyle{ R_G }[/math] велико настолько, что точки B и D можно считать не соединёнными (см. рисунок) ([math]\displaystyle{ R_G = \infty }[/math]).
Введём обозначения:
- [math]\displaystyle{ \varphi_A }[/math], [math]\displaystyle{ \varphi_B }[/math], [math]\displaystyle{ \varphi_C }[/math] и [math]\displaystyle{ \varphi_D }[/math] — соответственно потенциалы точек A, B, C и D, В;
- [math]\displaystyle{ U_{AC} }[/math] — напряжение между точками C и A, В:
- [math]\displaystyle{ U_{AC} = \varphi_A - \varphi_C ; }[/math]
- [math]\displaystyle{ U_{DB} }[/math] — напряжение между точками D и B, В:
- [math]\displaystyle{ U_{DB} = \varphi_D - \varphi_B ; }[/math]
- [math]\displaystyle{ R_{ADC} }[/math] — сопротивление участка ADC (последовательное соединение), Ом:
- [math]\displaystyle{ R_{ADC} = R_1 + R_2 ; }[/math]
- [math]\displaystyle{ R_{ABC} }[/math] — сопротивление участка ABC (последовательное соединение), Ом:
- [math]\displaystyle{ R_{ABC} = R_3 + R_x ; }[/math]
- [math]\displaystyle{ I_{ADC} }[/math], [math]\displaystyle{ I_{ABC} }[/math] — токи, протекающие на участках ADC и ABC соответственно, А.
По закону Ома токи [math]\displaystyle{ I_{ADC} }[/math], [math]\displaystyle{ I_{ABC} }[/math] равны:
- [math]\displaystyle{ I_{ADC} = \frac{ U_{AC} }{ R_{ADC} } = \frac{ U_{AC} }{ R_1 + R_2 } ; }[/math]
- [math]\displaystyle{ I_{ABC} = \frac{ U_{AC} }{ R_{ABC} } = \frac{ U_{AC} }{ R_3 + R_x } . }[/math]
По закону Ома падения напряжения на участках DC и BC равны:
- [math]\displaystyle{ U_{DC} = I_{ADC} \cdot R_2 ; }[/math]
- [math]\displaystyle{ U_{BC} = I_{ABC} \cdot R_x . }[/math]
Потенциалы в точках D и B равны:
- [math]\displaystyle{ \varphi_D = \varphi_C + U_{DC} = \varphi_C + I_{ADC} \cdot R_2 ; }[/math]
- [math]\displaystyle{ \varphi_B = \varphi_C + U_{BC} = \varphi_C + I_{ABC} \cdot R_x . }[/math]
Напряжение между точками D и B равно:
- [math]\displaystyle{ U_{DB} = \varphi_D - \varphi_B = \left( \varphi_C + I_{ADC} \cdot R_2 \right)\ - \left( \varphi_C + I_{ABC} \cdot R_x \right)\ = I_{ADC} \cdot R_2 - I_{ABC} \cdot R_x . }[/math]
Подставив выражения для токов [math]\displaystyle{ I_{ADC} }[/math] и [math]\displaystyle{ I_{ABC} }[/math], получим:
- [math]\displaystyle{ U_{DB} = \frac{ U_{AC} }{ R_1 + R_2 } \cdot R_2 - \frac{ U_{AC} }{ R_3 + R_x } \cdot R_x . }[/math]
Учитывая, что для «сбалансированного моста» [math]\displaystyle{ U_{DB} = 0 }[/math], получим:
- [math]\displaystyle{ 0 = \frac{ U_{AC} }{ R_1 + R_2 } \cdot R_2 - \frac{ U_{AC} }{ R_3 + R_x } \cdot R_x . }[/math]
Поместив слагаемые по разные стороны от знака равенства, получим:
- [math]\displaystyle{ \frac{ U_{AC} }{ R_1 + R_2 } \cdot R_2 = \frac{ U_{AC} }{ R_3 + R_x } \cdot R_x . }[/math]
Сократив [math]\displaystyle{ U_{AC} }[/math], получим:
- [math]\displaystyle{ \frac{ R_2 }{ R_1 + R_2 } = \frac{ R_x }{ R_3 + R_x } . }[/math]
Умножив на произведение знаменателей, получим:
- [math]\displaystyle{ R_2 \cdot ( R_3 + R_x ) = R_x \cdot ( R_1 + R_2 ) . }[/math]
Раскрыв скобки, получим:
- [math]\displaystyle{ R_2 \cdot R_3 + R_2 \cdot R_x = R_x \cdot R_1 + R_x \cdot R_2 . }[/math]
После вычитания [math]\displaystyle{ R_x \cdot R_2 }[/math] получим:
- [math]\displaystyle{ R_2 \cdot R_3 = R_1 \cdot R_x . }[/math]
Выразив [math]\displaystyle{ R_x }[/math], получим:
- [math]\displaystyle{ R_x = \frac{ R_2 \cdot R_3 }{ R_1 }. }[/math]
В данном случае мостовая схема рассматривалась, как комбинация двух делителей, а влияние гальванометра считалось пренебрежимо малым.
Общее сопротивление без выполнения условия баланса
В случае, если условие баланса не выполнено, расчёт общего сопротивления довольно громоздкий.
Пользуясь правилами Кирхгофа, получаем систему уравнений:
[math]\displaystyle{ \begin{cases} I_\Sigma = I_1 + I_4 = I_2 + I_3 \\ I_5 = I_1 - I_2 = I_4 - I_3 \\ R_\Sigma \cdot I_\Sigma = R_1 \cdot I_1 + R_2 \cdot I_2 = R_3 \cdot I_3 + R_4 \cdot I_4 \\ R_5 \cdot I_5 = R_4 \cdot I_4 - R_1 \cdot I_1 = R_2 \cdot I_2 - R_3 \cdot I_3 \end{cases} }[/math]
Тогда после исключения из системы всех токов получим окончательный результат, представленный в наиболее кратком виде:
[math]\displaystyle{ R_\Sigma = \frac{\sum_{1=i\lt j\lt k}^5 R_i R_j R_k - R_5 \left(R_1 R_4 + R_2 R_3 \right)}{\sum_{1=i\lt j}^5 R_i R_j - \left(R_1 R_2 + R_3 R_4 \right)}, }[/math]
где в суммах в числителе и в знаменателе суммируются все возможные комбинации из произведений сопротивлений без повторений сомножителей (всего таких комбинаций по десять).
Схемы подключения
На практике для измерения сопротивления с помощью мостовых схем применяют двухпроводное и четырёхпроводное подключение.
Двухпроводная схема подключения применяется при измерениях сопротивлений величиной выше 10 Ом. К точкам B и C (см. рисунок) подключаются по одному проводу.
Четырёхпроводная схема подключения применяется при измерении сопротивления величиной до 10 Ом. К точкам B и C (см. рисунок) подключаются по два провода. Это позволяет исключить влияние сопротивления проводов на величину измеренного сопротивления [math]\displaystyle{ R_x }[/math].
История создания
В 1833 году Самуэль Хантер Кристи (англ. Samuel Hunter Christie) предложил схему, позже получившую название «мост Уитстона».
В 1843 году схема была усовершенствована Чарльзом Уитстоном (англ. Charles Wheatstone)[2] и стала называться «мостом Уитстона».
В 1861 году лорд Кельвин использовал мост Уитстона для измерения малых сопротивлений.
В 1865 году Максвелл с помощью изменённого моста Уитстона измерял силу переменного тока.
В 1926 году Алан Блюмлейн усовершенствовал мост Уитстона и запатентовал. Новое устройство стали называть в честь изобретателя.
Классификация
В промышленности широко применяются уравновешенные и неуравновешенные измерительные мосты.
Работа уравновешенных мостов (наиболее точных) основана на «нулевом методе».
С помощью неуравновешенных мостов (менее точных) измеряемую величину определяют по показаниям измерительного прибора.
Измерительные мосты подразделяются на неавтоматические и автоматические.
В неавтоматических мостах балансирование производится вручную (оператором).
В автоматических балансировка моста происходит с помощью сервопривода по величине и знаку напряжения между точками D и B (см. рисунок).
Применение для измерения неэлектрических величин
Мост Уитстона часто используется для измерения самых разнообразных неэлектрических параметров, например:
- механических деформаций упругих элементов в тензометрии;
- температуры;
- освещённости;
- состава вещества, в том числе влажности и газовом анализе;
- теплопроводности и теплоёмкости и многого другого.
Принцип действия всех этих приборов основан на измерении сопротивления чувствительного резистивного элемента-датчика, сопротивление которого изменяется при изменении воздействующей на него неэлектрической величины. Резистивный датчик (датчики) включается электрически в одно или несколько плеч моста Уитстона и измерение неэлектрической величины сводится к измерению изменения сопротивления датчиков.
Применение моста Уитстона в этих приложениях обусловлено тем, что позволяет измерять относительно малое изменение сопротивления, то есть в случаях когда [math]\displaystyle{ \Delta R_x/R_x \ll 1. }[/math]
Обычно в современных измерительных приборах мост Уитстона подключается через аналого-цифровой преобразователь к цифровому вычислительному устройству, например, к микроконтроллеру, обрабатывающему сигнал моста. При обработке, как правило, производится линеаризация, масштабирование с преобразованием в численное значение неэлектрической величины в единицы её измерения, коррекция систематических погрешностей датчиков и измерительной схемы, индикация в удобном и наглядном для пользователя цифровом и/или машинно-графическом виде. Также может производиться статистическая обработка измерений, гармонический анализ и другие виды обработки.
Принцип работы тензометрических измерителей
Тензодатчики тензорезисторы применяются в:
- электронных весах;
- динамометрах
- измерителях давления (манометрах);
- измерителях крутящего момента на валах (торсиометрах);
- измерителях деформации деталей под воздействием механической нагрузки и др.
При этом тензорезисторы, наклеенные на упругие деформируемые детали включаются в плечи моста, а полезным сигналом является напряжение диагонали моста между точками D и B (см. рисунок).
Если выполняется соотношение:
- [math]\displaystyle{ R_1/R_2 = R_3/R_x , }[/math]
то независимо от напряжения на диагонали моста между точками A и C (напряжения) между точками D и B ([math]\displaystyle{ U_{DB} }[/math])) будет равно нулю:
- [math]\displaystyle{ U_{DB} = 0 . }[/math]
Но если [math]\displaystyle{ R_1/R_2 \ne R_3/R_x , }[/math] то на диагонали появится ненулевое напряжение («разбаланс» моста), однозначно связанное с изменением сопротивления тензорезистора, и, соответственно, с величиной деформации упругого элемента, при измерении разбаланса моста измеряют деформацию, а так как деформация связана, например, в случае весов, с весом взвешиваемого тела, то и в результате измеряют его вес.
Для измерения знакопеременных деформаций помимо тензодатчиков часто используют пьезоэлектрические датчики. Последние в этих приложениях вытеснили тензодатчики благодаря лучшим техническим и эксплуатационным характеристикам. Недостатком пьезодатчиков является непригодность их для измерения медленных или статических деформаций.
Измерения других неэлектрических величин
Описанный принцип измерения деформации с помощью тензорезисторов в тензометрии сохраняется для измерения иных неэлектрических величин с применением других резистивных датчиков, сопротивление которых изменяется под воздействием неэлектрической величины.
- Измерение температуры
В этих приложениях применяются резистивные датчики, находящиеся в тепловом равновесии с изучаемым телом, сопротивление датчиков изменяется при изменении их температуры. Также применяются датчики не контактирующие непосредственно с изучаемым телом, а измеряющие интенсивность теплового излучения от объекта, например, болометрические пирометры.
В качестве термочувствительных датчиков обычно используются резисторы, изготовленные из металлов — термометры сопротивления, имеющие положительный температурный коэффициент сопротивления, или полупроводниковые — терморезисторы с отрицательным температурным коэффициентом сопротивления.
Косвенно через измерение температуры также производится измерение теплопроводности, теплоёмкости, скорости потоков газов и жидкостей в термоанемометрах и измерение иных неэлектрических величин, связанных с температурой, например, концентрации компонента в газовой смеси с помощью термокаталитических датчиков и датчиков теплопроводности в газовой хроматографии.
- Измерение потоков излучения
В фотометрах применяются датчики, изменяющие своё сопротивление в зависимости от освещённости — фоторезисторы. Также существуют резистивные датчики для измерения потоков ионизирующих излучений.
Модификации
Используя мост Уитстона, можно с большой точностью измерять сопротивление.
Различные модификации моста Уитстона позволяют измерять другие физические величины:
- ёмкость;
- индуктивность;
- импеданс;
- концентрацию газов;
- и другое.
Прибор explosimeter (англ.) позволяет определить, превышена ли допустимая концентрация горючих газов в воздухе.
Мост Кельвина (англ. Kelvin bridge), также известный как мост Томсона (англ. Thomson bridge), позволяет измерять малые сопротивления, изобретён Томсоном.

Прибор Максвелла позволяет измерять силу переменного тока, изобретён Максвеллом в 1865 году, усовершенствован Блюмлейном около 1926 года.
Мост Максвелла (англ. Maxwell bridge) позволяет измерять индуктивность.
Мост Фостера (англ. Carey Foster bridge) позволяет измерять малые сопротивления, описан Фостером (англ. Carey Foster) в документе, опубликованном в 1872 году.
Делитель напряжения Кельвина-Варли (англ. Kelvin–Varley divider) построен на основе моста Уитстона.
Промышленные образцы
В СССР и России Краснодарским заводом измерительных приборов выпускались следующие марки измерительных мостов с ручной наводкой на равновесие[3]:
- ММВ (измерения сопротивления проводников постоянному току);
- Р333 (измерение по схеме одинарного моста, определение места повреждения кабеля по схемам петли Муррея и Варлея);
- МО-62.
См. также
- Мост Шеринга — схема для измерения ёмкости.
- Потенциометр (англ. potentiometer) — прибор для измерения ЭДС.
- Омметр (англ. ohmmeter) — прибор для измерения сопротивления.
- Реохорд — устройство для измерения сопротивления и ЭДС.
Примечания
- ↑ Мостик Витстона // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ 2,0 2,1 Марио Льоцци История физики — М.: Мир, 1970 — С. 261.
- ↑ Электротехнический справочник, 1980, с. 190.
Литература
- Панфилов В. А. Электрические измерения. — Академия, 2006.
- Электротехнический справочник. В 3-x томах / Герасимов В. Г. и др. — 6-е издание. — М.: Энергия, 1980. — Т. 1. — 520 с.