Закон транзитивности термического равновесия
Закон транзитивности термического равновесия (нулевой закон, нулевое начало термодинамики) вводит в физику представление об эмпирической температуре как физической величине, пригодной для характеристики состояния очень многих макроскопических объектов[1][2][3][4][5][6][7][8][9][10][11]. Примером макроскопического объекта, не нуждающегося в использовании температуры и прочих термических величин для описания своего состояния, служит абсолютно твёрдое тело[12]. Термические системы, то есть макроскопические системы, к которым применимо понятие температуры, являются предметом изучения термодинамики, статистической физики и физики сплошных сред. Абсолютно твёрдое тело к термическим системам не относится.
Историческая справка
В 1925 г. Т. А. Афанасьева-Эренфест показала[13], что система законов термодинамики должна быть дополнена аксиомой о существовании термодинамического равновесия (постулат Афанасьевой): «…всякое начальное состояние системы, представляющее нарушенное равновесие, приводит в конце концов к равновесному состоянию»[14], а Р. Фаулер в 1931 г. в ходе дискуссии с индийским астрофизиком Саха и его сотрудником Зривартава (В. Srivartava) сформулировал ещё одну аксиому — о существовании температуры (постулат Фаулера)[15][11][16], за которой после выхода монографии Р. Фаулера и Э. Гуггенгейма[17] закрепилось не слишком удачное название «нулевое начало термодинамики», поскольку данный закон оказался хронологически последним из нумерованных законов термодинамики. До появления термина «минус первое начало термодинамики»[18], закрепившего за аксиомой о существовании термодинамического равновесия статус одного из основных законов термодинамики, постулаты Афанасьевой (минус первое начало термодинамики) и Фаулера (существование температуры[19]) одни авторы интерпретировали как составные части нулевого закона термодинамики[20][21][22] (далее из чисто дидактических соображений будет использована именно такая трактовка нулевого начала), тогда как другие авторы рассматривали эти постулаты как самостоятельные аксиомы[23][24][25][26], подразумевая под нулевым началом только закон транзитивности термического равновесия и его следствие — существование эмпирической температуры[4][16][27][28][29][30][8][9][31].
В отечественной литературе постулат о существовании термодинамического равновесия иногда называют первым исходным положением термодинамики, а закон транзитивности термического равновесия — вторым исходным положением термодинамики[23][25].
Постулат о существовании термодинамического равновесия
Первый из двух входящих в нулевой закон термодинамики постулатов — постулат о существовании термодинамического равновесия[22] — утверждает, что макроскопическая система, находящаяся в неизменных внешних условиях, всегда приходит самопроизвольно в состояние термодинамического равновесия, которое характеризуется тем, что:
- прекращаются всякие макроскопические изменения в системе; каждый параметр, характеризующий макроскопическое свойство системы, имеет постоянное во времени значение;
- система, перешедшая в состояние термодинамического равновесия, сколь угодно долго остаётся в этом состоянии; для нарушения равновесия необходимы внешние воздействия[32].
При термодинамическом равновесии выполняются частные равновесия: механическое, химическое, термическое и др., то есть установление частного равновесия есть необходимое условие равновесия термодинамического. Достаточные условия равновесия (условия устойчивости) рассматриваются в термодинамике. Сейчас же отметим, что при делении системы на две части (подсистемы) посредством перегородки с определёнными свойствами (жёсткой или подвижной, непроницаемой для химических составных частей системы или полупроницаемой, теплоизолирующей адиабатической или теплопроводящей диатермической)[33] условие соблюдения термодинамического равновесия для системы в целом можно свести к выполнению одного из частных равновесий между её подсистемами. Использование жёсткой и непроницаемой для вещества диатермической перегородки сводит условие термодинамического равновесия для всей системы к термическому равновесию её подсистем. Чтобы обойти трудности, связанные с попыткой дать строгое определение «теплопроводящей (диатермической) перегородке», будем считать этот термин базовым, то есть таким, для которого возможно только описательное определение, но не определение посредством других, более общих терминов, ибо таковых просто не существует.
Принцип термодинамической допустимости Путилова
Представляется уместным сделать следующее отступление, имеющее прямое отношение к последующему изложению. В термодинамике достаточно распространено использование для мысленных экспериментов разного рода воображаемых идеализированных тел, приспособлений и механизмов. То обстоятельство, что такой подход не приводит к противоречию между теорией и опытными данными, позволило К. А. Путилову сформулировать следующее положение[34]: в термодинамике допустимо пользоваться какими угодно воображаемыми идеализированными по своим свойствам телами и приспособлениями без риска, применяя эти представления в рассуждениях, прийти к неверным результатам, если предварительно доказано, что их реализация, как бы ни были неправдоподобны их свойства, не противоречила бы ни первому, ни второму началу термодинамики (принцип термодинамической допустимости Путилова[35]). Не претендуя на роль закона природы, этот принцип, тем не менее, не может быть выведен из законов термодинамики, и в случае своего применения с формальной точки зрения должен рассматриваться как один из постулатов термодинамики.
Закон транзитивности термического равновесия
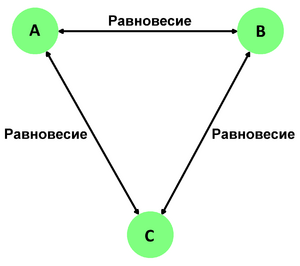
Второй из постулатов, входящих в нулевой закон, — закон транзитивности термического равновесия — гласит, что если две термодинамические системы, разделённые жёсткой и непроницаемой для вещества диатермической перегородкой, находятся в термическом равновесии между собой, то любая третья система, находящаяся в термическом равновесии с одной из первых двух систем, будет находиться также в термическом равновесии с другой из этих систем[22].
Может показаться, что закон транзитивности самоочевиден, но это не так (кусок янтаря, который потёрли шерстью, будет притягивать нейтральный шарик из бузины; так же будет себя вести и другой кусок янтаря, но два куска янтаря не будут притягиваться друг к другу).
Из закона транзитивности термического равновесия выводится[8][36] существование термодинамической функции состояния — эмпирической температуры, которая для всех систем, находящихся в состоянии термического равновесия, имеет одно и то же значение. С её помощью условие термического равновесия систем сводится к требованию равенства их температур. Возникающий при этом произвол устраняется выбором температурной шкалы. Затруднения, связанные с тем, что понимать под теплотой, получаемой/отдаваемой открытой системой (см. Неоднозначность понятий «теплота» и «работа»), ограничивают применимость закона транзитивности термического равновесия (а следовательно и обоснования существования эмпирической температуры) закрытыми системами.
Аксиоматический подход
При традиционном аксиоматическом подходе к построению термодинамики, позволяющем, в частности, обойтись без представлений о разного рода перегородках, постулат о транзитивности термического равновесия, из которого выводится существование эмпирической температуры, заменяют — по аналогии с первым и вторым началами термодинамики, каждое из которых обосновывает существование определённой функции состояния[37], — на постулат о существовании эмпирической температуры[38][4][5][2][3][39][40][6][7][10] — существует термодинамическая функция состояния, называемая эмпирической температурой и обладающая следующими свойствами[11]:
- температура представляет собой интенсивную термодинамическую величину;
- на качественном физиологическом уровне восприятия температура отражает наши ощущения тепла и холода; на качественном бытовом уровне — представления о степени нагретости тела;
- равенство температур двух подсистем есть необходимое и достаточное условие их термического равновесия и необходимое условие термодинамического равновесия системы в целом.
Полный перечень свойств температуры разнится для различных аксиоматических систем. Обратите внимание, что в основе фундаментального постулата рациональной термодинамики — постулата о существовании и свойствах абсолютной термодинамической температуры[41][42] — лежат нулевое начало в формулировке Зоммерфельда и представление о температуре как локальной макроскопической величине[43].
При более современном аксиоматическом подходе к построению термодинамики, основанном на переводе понятия «теплота» из базового во вторичное (то есть основанное на других базовых понятиях) и вспомогательное (то есть не являющееся жизненно необходимым для обоснования законов термодинамики), положения, относящиеся к температуре, включают в общую систему аксиом[44][45].
Примечания
- ↑ Физика. Большой энциклопедический словарь, 1998, с. 751.
- ↑ 2,0 2,1 Булидорова Г. В. и др., Физическая химия, 2012, с. 18.
- ↑ 3,0 3,1 Булидорова Г. В. и др., Основы химической термодинамики, 2011, с. 17.
- ↑ 4,0 4,1 4,2 Иванов А. Е., Иванов С. А., Механика. Молекулярная физика и термодинамика, 2012, с. 666.
- ↑ 5,0 5,1 Миронова Г. А. и др., Молекулярная физика и термодинамика в вопросах и задачах, 2012, с. 57.
- ↑ 6,0 6,1 Румер Ю. Б., Рывкин М. Ш., Термодинамика, статистическая физика и кинетика, 2000, с. 37.
- ↑ 7,0 7,1 Кушнырев В. И. и др., Техническая термодинамика и теплопередача, 1986, с. 12, 57—58, 83.
- ↑ 8,0 8,1 8,2 Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 11—12.
- ↑ 9,0 9,1 Вукалович М. П., Новиков И. И., Термодинамика, 1972, с. 11.
- ↑ 10,0 10,1 Радушкевич Л. В., Курс термодинамики, 1971, с. 5.
- ↑ 11,0 11,1 11,2 Зоммерфельд А., Термодинамика и статистическая физика, 1955, с. 11.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 40.
- ↑ Свиридонов М. Н., Развитие понятия энтропии в работах Т. А. Афанасьевой-Эренфест, 1971.
- ↑ Афанасьева-Эренфест Т. А., Необратимость, односторонность и второе начало термодинамики, 1928, с. 25.
- ↑ Фаулер Р., Гуггенгейм Э., Статистическая термодинамика, 1949, с. 79.
- ↑ 16,0 16,1 Mortimer R. G., Physical Chemistry, 2008, pp. 110—111.
- ↑ Fowler R.H., Guggenheim E.A., Statistical Thermodynamics, 1939.
- ↑ Brown H. R., Uffink J. The origins of time-asymmetry in thermodynamics: The minus first law (англ.) // Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics. — Elsevier, 2001. — Vol. 32, no. 4. — P. 525—538. — doi:10.1016/S1355-2198(01)00021-1.
- ↑ Любопытно, что называя нулевое начало постулатом о существовании температуры, авторы тем не менее могут обосновывать его посредством аксиомы о транзитивности термического равновесия (Манаков Н. Л., Мармо С. И., Лекции по термодинамике и статистической физике, ч. 1, 2003, с. 7—8).
- ↑ Квасников И. А., Молекулярная физика, 2009, с. 24—26.
- ↑ Квасников И. А., Термодинамика и статистическая физика, т. 1, 2002, с. 20—22.
- ↑ 22,0 22,1 22,2 Кубо Р., Термодинамика, 1970, с. 12.
- ↑ 23,0 23,1 Борщевский А. Я., Физическая химия, т. 1, 2017, с. 54—65.
- ↑ Круглов А. Б. и др., Руководство по технической термодинамике, 2012, с. 8—9.
- ↑ 25,0 25,1 Базаров И. П., Термодинамика, 2010, с. 17—19.
- ↑ Манаков Н. Л., Мармо С. И., Лекции по термодинамике и статистической физике, ч. 1, 2003, с. 6—8.
- ↑ Манаков Н. Л., Мармо С. И., Лекции по термодинамике и статистической физике, ч. 1, 2003, с. 7—8.
- ↑ Пригожин И., Кондепуди Д., Современная термодинамика, 2002, с. 20.
- ↑ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 30.
- ↑ Новиков И. И., Термодинамика, 1984, с. 11—12.
- ↑ Pippard A. B., Elements of classical thermodynamics, 1966, p. 9.
- ↑ Самойлович А. Г., Термодинамика и статистическая физика, 1955, с. 10.
- ↑ Физическая энциклопедия, т. 4, 1994, с. 196.
- ↑ Путилов К. А., Термодинамика, 1971, с. 201.
- ↑ Карякин Н. В., Основы химической термодинамики, 2003, с. 322.
- ↑ Леонтович М. А. Введение в термодинамику, 1983, с. 29—32.
- ↑ Рудой Ю. Г., Математическая структура равновесной термодинамики и статистической механики, 2013, с. 70.
- ↑ Кудинов И. В., Стефанюк Е. В., Теоретические основы теплотехники, ч. 1, 2013, с. 4.
- ↑ Розман Г. А., Термодинамика и статистическая физика, 2003, с. 10.
- ↑ Кудинов В. А., Карташов Э. М., Техническая термодинамика, 2001, с. 6.
- ↑ Максимов Л. А. и др., Лекции по статистической физике, 2009, с. 5—6.
- ↑ Трусделл К., Первоначальный курс рациональной механики сплошных сред, 1975, с. 400.
- ↑ Локальная макроскопическая величина характеризует мысленно выделяемую область (элементарный объём) сплошной среды (континуума), размеры которой бесконечно малы по сравнению с неоднородностями среды и бесконечно велики по отношению к размерам частиц (атомов, ионов, молекул и т. п.) этой среды (Жилин П. А., Рациональная механика сплошных сред, 2012, с. 84)
- ↑ Giles R., Mathematical Foundations of Thermodynamics, 1964.
- ↑ Lieb E. H., Yngvason J. The physics and mathematics of the second law of thermodynamics (англ.) // Physics Reports. — Elsevier, 1999. — Vol. 310, no. 1. — P. 1—96. — doi:10.1016/S0370-1573(98)00082-9.
Литература
- Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (нем.) // Zeitschrift für Physik. — 1925. — Vol. 33, Nr. 1. — P. 933–945.
- Ehrenfest-Afanassjewa T. Berichtigung zu der Arbeit: Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (нем.) // Zeitschrift für Physik. — 1925. — Vol. 34, Nr. 1. — P. 638.
- Ehrenfest-Afanassjewa T. Die Grundlagen der Thermodynamik. — Leiden: E.J. Brill, 1956. — XII + 131 с.
- Fowler R.H., Guggenheim E.A. Statistical Thermodynamics: A Version of Statistical mechanics for Students of Physics and Chemistry. — Cambridge: University Press, 1939. — 693 p.
- Giles R. Mathematical Foundations of Thermodynamics. — Oxford—London—New York—Paris: Pergamon Press, 1964. — Vol. 53. — xiv + 237 p. — (International series of monographs on pure and applied mathematics. General Editors: I.N. Sneddon, M. Stark and S. Ulam).
- Mortimer Robert G. Physical Chemistry. — 3. — Amsterdam e. a.: Elsevier Academic Press, 2008. — xviii + 1385 p. — ISBN 978-0-12-370617-1.
- Pippard A. B. Elements of classical thermodynamics. — Cambridge: Cambridge University Press, 1966. — viii + 165 p.
- Афанасьева-Эренфест Т. А. Необратимость, односторонность и второе начало термодинамики // Журнал прикладной физики. — 1928. — Vol. 5, № 3–4. — P. 3—30.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
- Булидорова Г. В., Галяметдинов Ю. Г., Ярошевская Х. М., Барабанов В. П. Основы химической термодинамики (к курсу физической химии). — Казань: Изд-во Казан. гос. технол. ун-та, 2011. — 218 с. — ISBN 978-5-7882-1151-0.
- Булидорова Г. В., Галяметдинов Ю. Г., Ярошевская Х. М., Барабанов В. П. Физическая химия. — Казань: Изд-во Казан. нац. исслед. технол. ун-та, 2012. — 396 с. — ISBN 978-5-7882-1367-5.
- Вукалович М. П., Новиков И. И. Термодинамика. — М.: Машиностроение, 1972. — 671 с.
- Жилин П. А. Рациональная механика сплошных сред. — 2-е изд. — СПб.: Изд-во Политехн. ун-та, 2012. — 584 с. — ISBN 978-5-7422-3248-3.
- Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
- Зоммерфельд А. Термодинамика и статистическая физика / Пер. с нем. — М.: Изд-во иностр. лит-ры, 1955. — 480 с.
- Иванов А. Е., Иванов С. А. Механика. Молекулярная физика и термодинамика. — М.: Кнорус, 2012. — 950 с. — ISBN 978-5-406-00525-5.
- Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1.
- Квасников И. А. Молекулярная физика. — М.: Эдиториал УРСС, 2009. — 232 с. — ISBN 978-5-901006-37-2.
- Квасников И. А. Термодинамика и статистическая физика. Т. 1: Теория равновесных систем: Термодинамика. — 2-е изд., сущ. перераб. и доп. — М.: Едиториал УРСС, 2002. — 240 с. — ISBN 5-354-00077-7.
- Круглов А. Б., Радовский И. С., Харитонов В. С. Руководство по технической термодинамике с примерами и задачами. — 2-е изд., пересмотр. и доп. — М.: НИЯУ МИФИ, 2012. — 156 с. — ISBN 978-5-7262-1694-2.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Кудинов В. А., Карташов Э. М. Техническая термодинамика. — 2-е изд., испр. — М.: Высшая школа, 2001. — 262 с. — ISBN 5-06-003712-6.
- Кудинов И. В., Стефанюк Е. В. Теоретические основы теплотехники. Часть 1. Термодинамика. — Самара: СГАСУ, 2013. — 172 с. — ISBN 978–5–9585–0553–1, 978–5–9585–0554–8.
- Кушнырев В. И., Лебедев В. И., Павленко В. А. Техническая термодинамика и теплопередача. — М.: Стройиздат, 1986. — 464 с.
- Леонтович М. А. Введение в термодинамику. Статистическая физика. — М.: Наука, 1983. — 416 с.
- Манаков Н. Л., Мармо С. И. Лекции по термодинамике и статистической физике. Часть I. — Воронеж: ВГУ, 2003. — 81 с.
- Максимов Л. А., Михеенков А. В., Полищук И. Я. Лекции по статистической физике. — Долгопрудный: МФТИ, 2009. — 224 с.
- Миронова Г. А., Брандт Н. Н., Салецкий А. М. Молекулярная физика и термодинамика в вопросах и задачах. — СПб.—М.—Краснодар: Лань, 2012. — 475 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1195-5.
- Новиков И. И. Термодинамика. — М.: Машиностроение, 1984. — 592 с.
- Петров Н., Бранков Й. Современные проблемы термодинамики. — Пер. с болг. — М.: Мир, 1986. — 287 с.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур / Пер. с англ. — М.: Мир, 2002. — 461 с. — (Лучший зарубежный учебник). — ISBN 5-03-003538-9.
- Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
- Радушкевич Л. В. Курс термодинамики. — М.: Просвещение, 1971. — 288 с.
- Розман Г. А. Термодинамика и статистическая физика. — Псков: Пск. гос. пед. ин-т, 2003. — 160 с. — ISBN 5-7615-0383-2.
- Рудой Ю. Г. Математическая структура равновесной термодинамики и статистической механики. — М.—Ижевск: Институт компьютерных исследований, 2013. — 368 с. — ISBN 978-5-4344-0159-3.
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. — 2-е изд., испр. и доп. — Новосибирск: Изд-во Носиб. ун-та, 2000. — 608 с. — ISBN 5-7615-0383-2.
- Самойлович А. Г. Термодинамика и статистическая физика. — 2-е изд. — М.: Гостехиздат, 1955. — 368 с.
- Свиридонов М. Н. Развитие понятия энтропии в работах Т. А. Афанасьевой-Эренфест // История и методология естественных наук. Выпуск X. Физика. — Издательство МГУ, 1971. — С. 112—129.
- Трусделл К. Первоначальный курс рациональной механики сплошных сред / Пер. с англ. под. ред. П. А. Жилина и А. И. Лурье. — М.: Мир, 1975. — 592 с.
- Фаулер Р., Гуггенгейм Э. Статистическая термодинамика / Под. ред. В. Г. Левича. — М.: Издательство иностранной литературы, 1949. — 612 с.
- Физика. Большой энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4: Пойнтинга—Робертсона эффект — Стримеры. — 704 с. — ISBN 5-85270-087-8.