Задача со счастливым концом

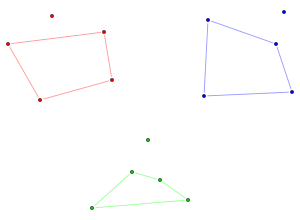
Задача со счастливым концом: любое множество из пяти точек содержит вершины выпуклого четырёхугольника.

Задача со счастливым концом — утверждение о том, что любое множество из пяти точек на плоскости в общем положении имеет подмножество из четырёх точек, которые являются вершинами выпуклого четырёхугольника.

История

Этот результат комбинаторной геометрии назван Палом Эрдёшем «задачей со счастливым концом», поскольку решение проблемы завершилось свадьбой Дьёрдя Секереша и Эстер Клейн (венг. Eszter Klein). Известна также как «теорема Эрдёша — Секереша о выпуклых многоугольниках».

Обобщения результата на произвольное число точек являются предметом интереса математиков XX и XXI веков.

Доказательство

Если не менее четырёх точек образуют выпуклую оболочку, в качестве выпуклого четырёхугольника можно выбрать любой набор из четырёх точек оболочки. В противном случае имеется треугольник и две точки внутри него. Прямая, проходящая через две внутренние точки, в силу общего положения точек не пересекает одну из сторон треугольника. Вершины этой стороны и две внутренние точки образуют выпуклый четырёхугольник.

Многоугольники с произвольным числом вершин

Эрдёш и Секереш обобщили этот результат на произвольное число точек, что является оригинальным развитием теории Рамсея. Они также выдвинули «гипотезу Эрдёша — Секереша» — точную формулу для максимального числа вершин выпуклого многоугольника, обязательно существующего в множестве из заданного числа точек в общем положении.

Восемь точек в общем положении для которых нет выпуклого пятиугольника.

В (Erdős & Szekeres 1935) доказано следующее обобщение: для любого натурального [math]\displaystyle{ N }[/math], всякое достаточно большое множество точек в общем положении на плоскости имеет подмножество [math]\displaystyle{ N }[/math] точек, которые являются вершинами выпуклого многоугольника. Это доказательство появилось в той же статье, где доказывается теорема Эрдёша — Секереша о монотонных подпоследовательностях в числовых последовательностях.

Размер множества как функция числа вершин многоугольника

Пусть [math]\displaystyle{ f(N) }[/math] означает минимальное [math]\displaystyle{ M }[/math], для которого любое множество из [math]\displaystyle{ M }[/math] точек в общем положении содержит выпуклый [math]\displaystyle{ N }[/math]-угольник. Известно, что:

• [math]\displaystyle{ f(3) = 3 }[/math], очевидно.
• [math]\displaystyle{ f(4) = 5 }[/math], доказала Эстер Секереш.
• [math]\displaystyle{ f(5) = 9 }[/math], согласно (Erdős & Szekeres 1935), это первым доказал Э. Макаи; первое опубликованное доказательство появилось в (Kalbfleisch, Kalbfleisch & Stanton 1970). Множество из восьми точек, не содержащее выпуклый пятиугольник, на иллюстрации показывает, что [math]\displaystyle{ f(5) \gt 8 }[/math]; сложнее доказать, что любое множество из девяти точек в общем положении содержит выпуклый пятиугольник.
• [math]\displaystyle{ f(6) = 17 }[/math], это было доказано в (Szekeres & Peters 2006). В работе реализован сокращённый компьютерный перебор возможных конфигураций из 17 точек.
• Значения [math]\displaystyle{ f(N) }[/math] неизвестны для [math]\displaystyle{ N \gt 6 }[/math].

Гипотеза Эрдёша — Секереша о минимальном числе точек

Исходя из известных значений [math]\displaystyle{ f(N) }[/math] для [math]\displaystyle{ N = 3, 4, 5 }[/math], Эрдёш и Секереш предположили, что:

[math]\displaystyle{ f(N) = 1 + 2^{N-2} }[/math] для всех [math]\displaystyle{ N }[/math].

Эта гипотеза не доказана, но известны оценки сверху и снизу.

Оценки скорости роста f(N)

Конструктивным построением авторы гипотезы сумели позднее доказать оценку снизу, совпадающую с гипотетическим равенством:

[math]\displaystyle{ f(N) \geq 1 + 2^{N-2} }[/math], (Erdős & Szekeres 1961)

Однако наилучшая известная оценка сверху при [math]\displaystyle{ N \ge 7 }[/math] не является близкой:

[math]\displaystyle{ f(N) \leq {2N-5 \choose N-2} + 1 = O\left(\frac{4^N}{\sqrt N}\right) }[/math], (Tóth & Valtr 2005)

(использованы биномиальные коэффициенты).

Пустые многоугольники

Интересен также вопрос о том, содержит ли достаточно большое множество точек в общем положении пустой выпуклый четырёхугольник, пятиугольник, и так далее. То есть многоугольник, не содержащий внутренних точек.

Если внутри четырёхугольника, существующего согласно теореме со счастливым концом, есть точка, то, соединив эту точку с двумя вершинами диагонали, мы получим два четырёхугольника, один из которых выпуклый и пустой. Таким образом, пять точек в общем положении содержат пустой выпуклый четырёхугольник, как видно на иллюстрации. Любые десять точек в общем положении содержит пустой выпуклый пятиугольник (Harborth 1978). Однако существуют сколь угодно большие множества точек в общем положении, которые не содержат пустой выпуклый семиугольник.(Horton 1983)

Таким образом, задача о пустых многоугольниках не является проблемой теории Рамсея и в принципе решена.

Вопрос о существовании пустого шестиугольника долгое время оставался открытым. Но в (Nicolás 2007) и (Gerken 2008) было доказано, что всякое достаточно большое множество точек в общем положении содержит пустой шестиугольник. Сегодня известно, что это множество должно содержать не более f(9) (предположительно 129) и не менее 30 точек.(Overmars 2003).

Ссылки

• Happy ending problem Архивная копия от 25 сентября 2006 на Wayback Machine and Ramsey-theoretic proof of the Erdős-Szekeres theorem on PlanetMath
• Weisstein, Eric W. Happy End Problem (англ.) на сайте Wolfram MathWorld.