Матрица достижимости

Матрица достижимости простого ориентированного графа [math]\displaystyle{ G=(V, A) }[/math] — бинарная матрица замыкания по транзитивности отношения [math]\displaystyle{ A }[/math] (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.

Способы построения матрицы достижимости

Перемножение матриц

Пусть дан простой граф [math]\displaystyle{ G=(V, A) }[/math], матрица смежности которого есть [math]\displaystyle{ \mathbf A = (a_{ij})_{n \times n} }[/math], где [math]\displaystyle{ a_{ij} = 1 \Leftrightarrow (i, j) \in A }[/math]. Матрица смежности даёт информацию о всех путях длины 1 (то есть дугах) в орграфе. Для поиска путей длины 2 можно найти композицию отношения [math]\displaystyle{ A }[/math] с самим собой:

[math]\displaystyle{ A\circ A = \bigl \{ (a, c): \exists b \in V: (a, b),\ (b, c) \in A \bigr \} }[/math].

По определению, матрица композиции отношений [math]\displaystyle{ A \circ A }[/math] есть [math]\displaystyle{ \mathbf{A^2} = ({a^2}_{ij})_{n \times n}=\Bigl (\sum_k a_{ik} a_{kj} \Bigr )=\Bigl ( (a_{i1} \land a_{1j}) \lor (a_{i2} \land a_{2j} ) \lor \ldots \lor (a_{in} \land a_{nj}) \Bigr ) }[/math], где [math]\displaystyle{ \land }[/math] — конъюнкция, а [math]\displaystyle{ \lor }[/math] — дизъюнкция.

После нахождения матриц [math]\displaystyle{ \mathbf A^k }[/math] композиций [math]\displaystyle{ \underbrace {A \circ \ldots \circ A}_k }[/math] для всех [math]\displaystyle{ k }[/math], [math]\displaystyle{ 1 \leq k \leq n-1 }[/math] будет получена информация о всех путях длины от [math]\displaystyle{ 1 }[/math] до [math]\displaystyle{ n-1 }[/math]. Таким образом, матрица [math]\displaystyle{ \mathbf {R(G)} = \mathbf E \lor \mathbf{A} \lor \mathbf{A^2} \lor \ldots \lor \mathbf{A^{n-1}} = ({a^*}_{ij})_{n \times n} = ({a}_{ij} \lor {a^2}_{ij} \lor \ldots \lor {a^{n-1}}_{ij}) }[/math] есть искомая матрица достижимости, где [math]\displaystyle{ \mathbf E }[/math] — единичная матрица.

[math]\displaystyle{ \mathbf E = \begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} }[/math]

Случай нескольких путей

Если булевы операции [math]\displaystyle{ \lor, \land }[/math] дизъюнкции и конъюнкции заменить обычными алгебраическими операциями [math]\displaystyle{ +, \times }[/math] сложения и умножения соответственно, нахождение матрицы достижимости [math]\displaystyle{ \mathbf{R(G)} }[/math] сведётся к обычному пошаговому перемножению матриц с последующим сложением результатов каждого шага. Тогда получившаяся матрица [math]\displaystyle{ \mathbf{R(G)} }[/math] будет состоять не только из 0 и 1 и будет характеризовать не только наличие путей между вершинами, но уже и количество таких путей. В таком случае можно разрешить наличие кратных рёбер в графе.

Пример

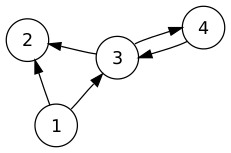
Рассмотрим простой связный ориентированный граф [math]\displaystyle{ G=(V=\{1, 2, 3, 4\}, A =\{(1, 2), (1, 3), (3, 2), (3, 4), (4, 3)\}) }[/math]. Он имеет матрицу смежности [math]\displaystyle{ \mathbf A }[/math] вида:

[math]\displaystyle{ \mathbf A = \begin{pmatrix} 0&1&1&0 \\ 0&0&0&0 \\ 0&1&0&1 \\ 0&0&1&0 \end{pmatrix} }[/math]

Найдём булевы степени этой матрицы [math]\displaystyle{ \mathbf{A^2} }[/math], [math]\displaystyle{ \mathbf{A^3} }[/math]:

[math]\displaystyle{ \mathbf{A^2} = \begin{pmatrix} 0&1&0&1 \\ 0&0&0&0 \\ 0&0&1&0 \\ 0&1&0&1 \end{pmatrix} }[/math], [math]\displaystyle{ \mathbf{A^3} = \begin{pmatrix} 0&0&1&0 \\ 0&0&0&0 \\ 0&1&0&1 \\ 0&0&1&0 \end{pmatrix} }[/math],

Получим матрицу достижимости

[math]\displaystyle{ \mathbf{R(G)} = \mathbf{E \lor A \lor A^2 \lor A^3} = \begin{pmatrix} 1&1&1&1 \\ 0&1&0&0 \\ 0&1&1&1 \\ 0&1&1&1 \end{pmatrix} }[/math]

Таким образом, из вершины [math]\displaystyle{ 1 }[/math] можно добраться в любую другую.

При использовании же алгебраических операций получится матрица

[math]\displaystyle{ \mathbf{R(G)} = \mathbf{E + A + A^2 + A^3} = \begin{pmatrix} 1&2&2&1 \\ 0&1&0&0 \\ 0&2&2&2 \\ 0&1&2&2 \end{pmatrix} }[/math]

Она показывает количество путей длины от 0 до 3 между вершинами орграфа.

Алгоритм Уоршелла

Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за [math]\displaystyle{ 2n^3 }[/math] шагов — алгоритм Уоршелла.

Связанные понятия

Матрица сильной связности

Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.

Построение матрицы сильной связности

Матрица сильной связности может быть построена из матрицы достижимости. Пусть [math]\displaystyle{ \mathbf E^* }[/math] — матрица достижимости орграфа [math]\displaystyle{ G=(V, E) }[/math]. Тогда матрица сильной связности [math]\displaystyle{ \mathbf C }[/math] состоит из элементов [math]\displaystyle{ (c_{ij}) = \left ( (e_{ij}) \land (e_{ji}) \right ) }[/math].

Пример

Рассмотрим тот же граф, что и ранее.

Его матрица достижимости:

[math]\displaystyle{ \mathbf{E^*} = \begin{pmatrix} 1&1&1&1 \\ 0&1&0&0 \\ 0&1&1&1 \\ 0&1&1&1 \end{pmatrix} }[/math]

Из неё получаем матрицу сильной связности:

[math]\displaystyle{ \mathbf{C} = \begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&1 \\ 0&0&1&1 \end{pmatrix} }[/math]

Вершины 3 и 4 сильно связаны друг с другом и сами с собой.

Матрица связности графа

Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.

Матрица контрдостижимости

Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.

Примечания