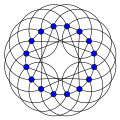
Граф Шрикханде
| граф Шрикханде | |
|---|---|
 | |
| Назван в честь | С. С. Шрикханде |
| Вершин | 16 |
| Рёбер | 48 |
| Радиус | 2 |
| Диаметр | 2 |
| Обхват | 3 |
| Автоморфизмы | 192 |
| Хроматическое число | 4 |
| Хроматический индекс | 6 |
| Свойства |
Сильно регулярный Гамильтонов Симметричный Эйлеров Целый |
| Книжная толщина | 4 |
| Число очередей | 3 |
Граф Шрикханде — граф, найденный С. С. Шрикханде (англ.) в 1959 году[1][2]. Граф сильно регулярен, имеет 16 вершин и 48 рёбер и каждая вершина имеет степень 6. Каждая пара узлов имеет ровно два общих соседа, независимо от того, связана эта пара ребром или нет.
Построение
Граф Шрикханде можно построить как граф Кэли, в котором множество вершин — это [math]\displaystyle{ \mathbb{Z}_4 \times \mathbb{Z}_4 }[/math], а две вершины связаны тогда и только тогда, когда разность находится в [math]\displaystyle{ \{\pm( 1,0),\pm(0,1),\pm (1,1)\} }[/math].
Свойства
В графе Шрикханде любые две вершины I и J имеют двух различных общих соседей (исключая сами вершины I и J), что выполняется вне зависимости от того, смежны ли I и J, или нет. Другими словами, граф сильно регулярен и его параметрами являются: {16,6,2,2}, то есть [math]\displaystyle{ \lambda = \mu = 2 }[/math]. Из этого равенства следует, что граф ассоциирован с симметричными сбалансированными неполными блок-схемами (англ. Balanced Incomplete Block Designs, BIBD). Граф Шрикханде разделяет эти параметры с точно одним другим графом, 4×4 ладейным графом, то есть рёберным графом L(K4,4) полного двудольного графа K4,4. Последний граф является единственным рёберным графом L(Kn, n), для которого параметры сильной регулярности не определяют этот граф единственным образом, и граф делит их с другим графом, а именно графом Шрикханде (который не является ладейным графом)[2][3].
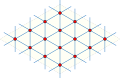
Граф Шрикханде локально шестиуголен. То есть соседи каждой вершины образуют цикл из шести вершин. Как и любой локально цикличный граф, граф Шрикханде является 1-мерным остовом[англ.] триангуляции Уитни некоторой поверхности. В случае графа Шрикханде эта поверхность является тором, в котором каждая вершина окружена шестью треугольниками[4] Таким образом, граф Шрикханде — это тороидальный граф. Вложение образует регулярное отображение в тор с 32 треугольными гранями. Остов дуального графа этого отображения (как вложенного в тор) — граф Дика, кубический симметричный граф.
Граф Шрикханде не является дистанционно-транзитивным. Это самый маленький дистанционно-регулярный граф, не являющийся дистанционно-транзитивным[5].
Группа автоморфизмов графа Шрикханде имеет порядок 192. Она действует транзитивно на вершины, на рёбра и дуги графа. Поэтому граф Шрикханде является симметричным графом.
Характеристический многочлен графа Шрикханде равен [math]\displaystyle{ (x-6)(x-2)^6(x+2)^9 }[/math]. Таким образом, граф Шрикханде является целым графом — его спектр состоит всецело из целых чисел.
Граф имеет книжную толщину 4 и число очередей 3[6].
Галерея
-
Граф Шрикханде является тороидальным.
-
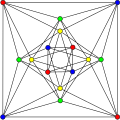
Хроматическое число графа Шрикханде равно 4.
-
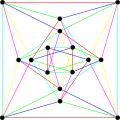
Хроматический индекс графа Шрикханде равен 6.
-
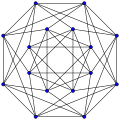
Граф Шрикханде, нарисованный симметрично.
-
Граф Шрикханде гамильтонов.
Примечания
- ↑ Weisstein, Eric W. Shrikhande Graph (англ.) на сайте Wolfram MathWorld.
- ↑ 2,0 2,1 Shrikhande, 1959, с. 781–798.
- ↑ Harary, 1972, с. 79.
- ↑ Brouwer A. E. Shrikhande graph Архивная копия от 9 марта 2014 на Wayback Machine.
- ↑ Brouwer, Cohen, Neumaier, 1989, с. 104–105, 136.
- ↑ Wolz, 2018.
Литература
- Shrikhande S. S. The uniqueness of the L2 association scheme // Annals of Mathematical Statistics. — 1959. — Т. 30. — С. 781–798. — doi:10.1214/aoms/1177706207. — .
- Frank Harary. Graph Theory. — Massachusetts: Addison-Wesley, 1972.
- Харари Ф. Теория графов. — М.: «Мир», 1973.
- , ISBN 0-521-43594-3
- Brouwer A. E., Cohen A. M., Neumaier A. Distance-Regular Graphs. — New York: Springer-Verlag, 1989. — С. 104–105, 136.
- Jessica Wolz. Engineering Linear Layouts with SAT. — University of Tübingen, 2018. — (Master Thesis).
Ссылки
- The Shrikhande Graph Архивная копия от 24 ноября 2010 на Wayback Machine, Peter Cameron, August 2010.
Для улучшения этой статьи желательно: |