Граф Риба

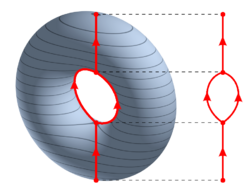
В теории графов, граф Риба некоторой функции описывает связность поверхностей уровня этой функции. Был введен Жоржем Рибом^[1]

Определение

Рассмотрим непрерывную функцию, заданную на компактном многообразии, [math]\displaystyle{ f: M\to R }[/math]. Прообраз точки [math]\displaystyle{ y\in R }[/math] является поверхностью уровня функции [math]\displaystyle{ f^{-1}(y)\subset M }[/math]. Две точки [math]\displaystyle{ x,x'\in M }[/math] называются эквивалентными, [math]\displaystyle{ x\!\sim x' }[/math], если они принадлежат одной компоненте связности поверхности уровня [math]\displaystyle{ f^{-1}(y) }[/math].

Граф Риба функции [math]\displaystyle{ f }[/math] — это факторпространство многообразия [math]\displaystyle{ M }[/math] по такому отношению эквивалентности, [math]\displaystyle{ G=M/\!\sim }[/math]. Вершинами графа являются компоненты связности критических уровней функции. Ориентация графа [math]\displaystyle{ G }[/math] определяется направлением градиента функции [math]\displaystyle{ f }[/math].

Свойства

Следующие свойства графа Риба были доказаны в его основополагающей работе^[1]:

Пусть на компактном [math]\displaystyle{ n }[/math]-мерном многообразии класса гладкости [math]\displaystyle{ C^2 }[/math] задана функция Морса f, все критические точки которой соответствуют разным критическим значениям функции. Множество таких функций открыто и плотно в пространстве всех функций. Обозначим [math]\displaystyle{ \Gamma }[/math] граф Риба этой функции. Тогда:

Вершинам степени 1 графа [math]\displaystyle{ \Gamma }[/math] в точности соответствуют критические точки функции f индекса 0 и n.
Если [math]\displaystyle{ n\ge 3 }[/math], вершина графа, соответствующая критическому уровню функции f, который содержит критическую точку индекса 1 и n-1, может иметь степень 2 или 3.
Если [math]\displaystyle{ n\,=2 }[/math], вершины графа, соответствующие критическим точкам индекса 1, могут иметь степень 2, 3 или 4.
Степень вершины графа, соответствующей критическому уровню функции f, который содержит критическую точку индекса, отличного от 0, 1, n-1 и n, всегда равна 2.

Эти свойства графа влекут любопытное свойство функций Морса, доказанное там же^[1]:

Обозначим через [math]\displaystyle{ \Omega_k }[/math] множество критических точек функции индекса k и n-k. Если [math]\displaystyle{ n\ge 3 }[/math], то [math]\displaystyle{ |\Omega_0|\le |\Omega_1|+2 }[/math].

Применение

Графы Риба используются в математике при изучении

топологической классификации функций Морса ^[2]
гамильтоновых систем ^[3]

Графы Риба и, в особенности, ациклические графы Риба, называемые контурными деревьями, находят широкое применение в компьютерных приложениях:

в компьютерном дизайне и геометрическом моделировании,
в геометрических моделях структуры данных и методах поиска в базах данных
в системах автоматизации проектных работ.

Примечания

↑ ^1,0 ^1,1 ^1,2 G. Reeb, Sur les points singuliers d’une forme de Pfaff complétement intégrable ou d’une fonction numérique. — C.R.A.S. Paris 222, 1946, pp. 847—849.[1] Архивная копия от 9 марта 2016 на Wayback Machine
↑ Шарко В. В. Гладкая и топологическая эквивалентность функций на поверхностях. // Український математичний журнал. 2003. Т. 55. № 5. С. 687—700.
↑ А. В. Болсинов, А. Т. Фоменко, Введение в топологию интегрируемых гамильтоновых систем, Наука, М., 1997.

[Reeb-1] 1,0 ^1,1 ^1,2 G. Reeb, Sur les points singuliers d’une forme de Pfaff complétement intégrable ou d’une fonction numérique. — C.R.A.S. Paris 222, 1946, pp. 847—849.[1] Архивная копия от 9 марта 2016 на Wayback Machine

[2] Шарко В. В. Гладкая и топологическая эквивалентность функций на поверхностях. // Український математичний журнал. 2003. Т. 55. № 5. С. 687—700.

[3] А. В. Болсинов, А. Т. Фоменко, Введение в топологию интегрируемых гамильтоновых систем, Наука, М., 1997.

[1]

[2]

[3]