H∞-управление
H на бесконечности или [math]\displaystyle{ \mathcal{H}_\infty }[/math] — метод теории управления для синтеза оптимальных регуляторов. Метод является оптимизационным, имеющим дело со строгим математическим описанием предполагаемого поведения замкнутой системы и её устойчивости. Метод примечателен своей строгой математической базой, оптимизационным характером и применимостью как к классическому, так и робастному управлению.
[math]\displaystyle{ \mathcal{H} }[/math] является нормой в пространстве Харди. «Бесконечность» говорит о выполнении минимаксных условий в частотной области. [math]\displaystyle{ \mathcal{H}_\infty }[/math]-норма динамической системы, имеющая смысл максимального усиления системы по энергии. В случае MIMO-систем она равна максимальному сингулярному числу передаточной функции системы, в случае SISO-систем она равна максимальному значению амплитуды её частотной характеристики.
Постановка задачи
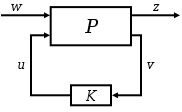
Сначала система должна быть приведена к стандартному виду:
Объект управления [math]\displaystyle{ \ P }[/math] имеет два входа, два внешних воздействия [math]\displaystyle{ \ w }[/math], которые включают задаточный сигнал и возмущения. Контролируемая переменная обозначена [math]\displaystyle{ \ u }[/math]. Это вектор выходных сигналов системы, состоящий из сигнала ошибки [math]\displaystyle{ \ z }[/math], который надо минимизировать, и измеренная переменная [math]\displaystyle{ \ v }[/math], которая используется в контуре управления. [math]\displaystyle{ \ v }[/math] используется в K для подсчёта переменной [math]\displaystyle{ \ u }[/math].
Уравнение системы:
- [math]\displaystyle{ \begin{bmatrix} z\\ v \end{bmatrix} = P(s)\, \begin{bmatrix} w\\ u\end{bmatrix} = \begin{bmatrix}P_{11}(s) & P_{12}(s)\\P_{21}(s) & P_{22}(s)\end{bmatrix} \, \begin{bmatrix} w\\ u\end{bmatrix} }[/math]
- [math]\displaystyle{ u = K(s) \, v }[/math]
Таким образом возможно выразить зависимость [math]\displaystyle{ \ z }[/math] от [math]\displaystyle{ \ w }[/math]:
- [math]\displaystyle{ z=F_l(P,K)\,w }[/math]
И далее:
- [math]\displaystyle{ F_l(P,K) = P_{11} + P_{12}\,K\,(I-P_{22}\,K)^{-1}\,P_{21} }[/math]
Таким образом, целью [math]\displaystyle{ \mathcal{H}_\infty }[/math]-оптимального управления является синтез такого контроллера [math]\displaystyle{ \ K }[/math], [math]\displaystyle{ \ F_l(P,K) }[/math], который минимизировал бы [math]\displaystyle{ \mathcal{H}_\infty }[/math]-норму системы. То же относится и к [math]\displaystyle{ \mathcal{H}_2 }[/math]-управлению. Норма на бесконечности матрицы[math]\displaystyle{ \ F_l(P,K) }[/math] определяется как:
- [math]\displaystyle{ ||F_l(P,K)||_\infty = \sup_\omega \bar{\sigma}(F_l(P,K)(j\omega)) }[/math]
где [math]\displaystyle{ \bar{\sigma} }[/math] — максимальное сингулярное число матрицы [math]\displaystyle{ \ F_l(P,K)(j\omega) }[/math].
Найденный таким образом контроллер является оптимальным в [math]\displaystyle{ \mathcal{H}_\infty }[/math]-смысле. Существует также ряд приложений, в которых решается так называемая «задача малого усиления (англ. small gain problem)». В рамках этой задачи необходимо найти такой контроллер, который бы обеспечивал выполнение условия
- [math]\displaystyle{ min(||F_l(P,K)||_\infty) \le 1 }[/math].
Эта задача иногда также называется «стандартной задачей [math]\displaystyle{ \mathcal{H}_\infty }[/math]-управления».
Преимущества и недостатки
H∞-управление имеет несколько особенностей в сравнении с другими методами синтеза робастных контроллеров. К преимуществам можно отнести:
- Метод работает с устойчивостью и чувствительностью системы.
- Простой одношаговый алгоритм.
- Точное формирование выходной частотной характеристики.
К недостаткам можно отнести то, что метод требует обращать особое внимание на параметрическую робастность объекта управления.
Свойства [math]\displaystyle{ \mathcal{H}_\infty }[/math]-контроллеров
1. Весовая функция [math]\displaystyle{ \mathcal{H}_\infty }[/math]-оптимального контроллера представляет собой фазовый фильтр, то есть для наименьшего сингулярного числа системы [math]\displaystyle{ \bar{ \sigma\ } }[/math] выполняется соотношение:
- [math]\displaystyle{ \bar{ \sigma\ }(F_l(P,K)) = 1 }[/math] для любого [math]\displaystyle{ \omega\ \in R }[/math]
2. [math]\displaystyle{ \mathcal{H}_\infty }[/math]-оптимальный контроллер имеет порядок максимум [math]\displaystyle{ \ n-1 }[/math], где [math]\displaystyle{ \ n }[/math] — порядок объекта управления.
Условия существования [math]\displaystyle{ \mathcal{H}_\infty }[/math]-контроллеров
Для того, чтобы существовал [math]\displaystyle{ \mathcal{H}_\infty }[/math]-контроллер в стандартной задаче:
- [math]\displaystyle{ min(||F_l(P,K)||_\infty) \le 1 }[/math]
необходимо и достаточно выполнение следующих условий:
1. Представим замкнутую систему в виде уравнений в пространстве состояний:
- [math]\displaystyle{ \dot{\mathbf{x}}(t) = A(t) \mathbf{x}(t) + B(t) \mathbf{u}(t) }[/math]
- [math]\displaystyle{ \mathbf{y}(t) = C(t) \mathbf{x}(t) + D(t) \mathbf{u}(t) }[/math]
Должен существовать закон пропорционального управления [math]\displaystyle{ \ F(s) = K }[/math] такой, чтобы наибольшее сингулярное число матрицы [math]\displaystyle{ \ D }[/math] замкнутой системы удовлетворяло неравенству [math]\displaystyle{ \sigma_n\ (D) \lt 1 }[/math]
2. Уравнение Риккати для управления
Уравнение Риккати для управления по состояниям должно иметь вещественное, положительно-определённое решение [math]\displaystyle{ P \ge 0 }[/math].
3. Уравнение Риккати для наблюдателя
Уравнение Риккати для наблюдателя, работающего в паре с контроллером, должно иметь вещественное, положительно-определённое решение [math]\displaystyle{ S \ge 0 }[/math].
4. Ограничение по собственным числам:
Наибольшее собственное число произведения двух решений (для контроллера и наблюдателя) уравнений Риккати должно быть меньше единицы: [math]\displaystyle{ \lambda_{max}(PS) \lt 1 }[/math]
См. также
Библиография
- Егупов Н. Д., Пупков К. А. Методы классической и современной теории автоматического управления. Синтез регуляторов систем автоматического управления. В 5 тт. Т. 3, Изд.2. 2004.616 с.
- R. Y. Chiang, Modern Robust Control Theory. Ph. D. Dissertation: USC,1988.