3-3 дуопризма
3-3 дуопризма Диаграмма Шлегеля | |
|---|---|
| Type | Однородная дуопризма |
| Символ Шлефли | {3}×{3} = {3}2 |
| Диаграммы Коксетера — Дынкина |    
|
| Ячеек | 6 треугольных призм |
| Граней | 9 квадратов, 6 треугольников |
| Рёбер | 18 |
| Вершин | 9 |
| Вершинная фигура |  Равногранный тетраэдр |
| Симметрия | Шаблон:Brackets = [6,2+,6], order 72 |
| Двойственный | 3-3 дуопирамида |
| Свойства | выпуклый, вершинно однородный, гранетранзитивный |
3-3 дуопризма или треугольная дуопризма, наименьшая из p-q дуопризм, это четырёхмерный многогранник, получающийся прямым произведением двух треугольников.
Многогранник имеет 9 вершин, 18 рёбер, 15 граней (9 квадратов и 6 треугольников) в 6 ячейках в форме треугольных призм. Он имеет диаграмму Коксетера 
и симметрию Шаблон:Brackets порядка 72. Его вершины и рёбра образуют [math]\displaystyle{ 3\times 3 }[/math] ладейный граф.
Гиперобъём
Гиперобъём однородной 3-3 дуопризмы с рёбрами длины a равен [math]\displaystyle{ V_4 = {3\over 16}a^4 }[/math]. Он вычисляется как квадрат площади правильного треугольника, [math]\displaystyle{ A = {\sqrt3\over 4}a^2 }[/math].
Изображения
|
|
|
|
|
|
|
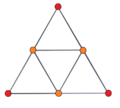
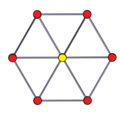
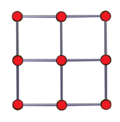
| Развёртка | Вершинная перспектива | 3D перспективная проекция с 2 различными вращениями |
|---|
Симметрия
В 5-мерных пространствах некоторые однородные многогранники имеют 3-3 дуопризму в качестве вершинных фигур, некоторые с неравными длинами рёбер, а потому с меньшей симметрией:
| Симметрия | Шаблон:Brackets, order 72 | [3,2], order 12 | ||
|---|---|---|---|---|
| Диаграмма Коксетера |
 
|
|
|
|
| Диаграмма Шлегеля |
|
|
|
|
| Название | t2α5 | t03α5 | t03γ5 | t03β5 |
Биспрямлённые 16-ячеечные соты также имеют 3-3 дуопризму в качестве вершинных фигур. Имеется три построения для сот с двумя меньшими симметриями.
| Симметрия | [3,2,3], порядок 36 | [3,2], порядок 12 | [3], порядок 6 |
|---|---|---|---|
| Диаграмма Коксетера |
|
 
|
 
|
| Косая ортогональная проекция |
|
|
|
Связанные комплексные многоугольники
Правильный комплексный многогранник 3{4}2, 
в [math]\displaystyle{ \mathbb{C}^2 }[/math] имеет вещественное представление как 3-3 дуопризма в 4-мерном пространстве. 3{4}2 имеет 9 вершин и 6 3-рёбер. Его группа симметрии 3[4]2 имеет порядок 18. Многогранник имеет также построение с меньшей симметрией или 3{}×3{} с симметрией 3[2]3 порядка 9. Эта симметрия возникает, если красные и синие 3-рёбра считать различными[1].
 Перспективная проекция |
 Ортогональная проекция с совпадающими центральными вершинами |
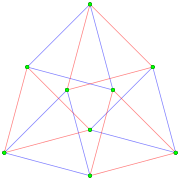 Ортогональная проекция со смещением, чтобы избежать наложение элементов. |
Связанные многогранники
3-3 дуопирамида
| 3-3 дуопирамида | |
|---|---|
| Type | Однородная двойственная дуопирамида |
| Символ Шлефли | {3}+{3} = 2{3} |
| Диаграмма Коксетера |  
|
| Ячейки | 9 равногранных тетраэдров |
| Грпани | 18 равнобедренных треугольников |
| Рёбер | 15 (9+6) |
| Вершин | 6 (3+3) |
| Симметрия | Шаблон:Brackets = [6,2+,6], order 72 |
| Двойственный | 3-3 дуопризма |
| Свойствия | выпуклый, вершинно однородный, гранетранзитивный |
Двойственный многогранник для 3-3 дуопризмы называется 3-3 дуопирамидой или треугольной дуопирамидой. Он имеет 9 ячеек в виде равногранных тетраэдров, 18 треугольных граней, 15 рёбер и 6 вершин.
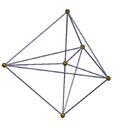
Многогранник можно рассматривать в ортогональной проекции как 6-угольник, в котором рёбра соединяют все пары вершин, точно как в 5-симплексе.
Связанный комплексный многоугольник
Комплексный многоугольник 2{4}3 имеет 6 вершин в [math]\displaystyle{ \mathbb{C}^2 }[/math] с вещественным представлением в [math]\displaystyle{ \mathbb{R}^4 }[/math] с тем же расположением вершин как у 3-3 дуопирамиды. Многогранник имеет 9 2-рёбер, соответствующих рёбрам 3-3 дуопирамиды, но 6 рёбер, соединяющих два треугольника, не включены. Его можно рассматривать в шестиугольной проекции с 3 наборами раскрашенных рёбер. Это расположение вершин и рёбер даёт полный двудольный граф, в котором каждая вершина одного треугольника связана с каждой вершиной другого. Граф называется также графом Томсена или 4-клеткой[2].
 2{4}3 с 6 вершинами (синими и красными) связанные 9 2-рёбрами в виде полного двудольного графа. |
 Граф имеет 3 набора из 3 рёбер, показанных цветом. |
См. также
- 3,4-дуопризма
- Тессеракт (4-4 дуопризма)
- 5,5-дуопризма
- Выпуклые правильные 4-мерные многогранники
- Дуоцилиндр
Примечания
- ↑ Coxeter, 1991.
- ↑ Coxeter, 1991, с. 110, 114.
Литература
- Coxeter H.S.M. Regular Polytopes. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
- Coxeter H.S.M. Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — С. 212-213. — ISBN 0-486-40919-8.
- Coxeter H.S.M. Regular Skew Polyhedra in Three and Four Dimensions // Proc. London Math. Soc.. — 1937. — Вып. 43. — С. 33–62.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 26 // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- N.W. Johnson. Uniform Polytopes. — 1991. — (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
- Catalogue of Convex Polychora, section 6 George Olshevsky
- Glossary for Hyperspace (Словарь терминов) George Olshevsky
- Apollonian Ball Packings and Stacked Polytopes // Discrete & Computational Geometry. — 2016. — Июнь (т. 55, вып. 4). — С. 801–826.
- H.S.M. Coxeter. Regular Complex Polytopes. — 2nd. — Cambridge University Press, 1991. — ISBN 978-0-521-39490-1.
Ссылки
- The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
- Polygloss – glossary of higher-dimensional terms
- Exploring Hyperspace with the Geometric Product
 | Для улучшения этой статьи желательно: |