Числа Лаха

Иллюстрация беззнаковых чисел Лаха для n и k между 1 и 4

Числа Лаха, открытые математиком из Словении Иво Лахом в 1955 — это коэффициенты, выражающие возрастающие факториалы через убывающие факториалы.

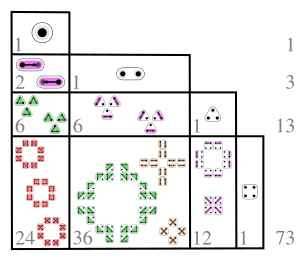
Беззнаковые числа Лаха имеют интересное значение в комбинаторике — они отражают число способов, каким множество из n элементов может быть разбито на k непустых упорядоченных подмножеств. Числа Лаха связаны с числами Стирлинга.

Беззнаковые числа Лаха (последовательность A105278 в OEIS):

[math]\displaystyle{ L(n,k) = {n-1 \choose k-1} \frac{n!}{k!}. }[/math]

Числа Лаха со знаками (последовательность A008297 в OEIS):

[math]\displaystyle{ L'(n,k) = (-1)^n {n-1 \choose k-1} \frac{n!}{k!}. }[/math]

L(n, 1) всегда равно n!. В вышеупомянутой интерпретации разбиения множества {1, 2, 3} на 1 множество может быть осуществлено 6 способами:

{(1, 2, 3)}, {(1, 3, 2)}, {(2, 1, 3)}, {(2, 3, 1)}, {(3, 1, 2)}, {(3, 2, 1)}

L(3, 2) соответствует 6 разбиениям на два упорядоченных множества:

{(1), (2, 3)}, {(1), (3, 2)}, {(2), (1, 3)}, {(2), (3, 1)}, {(3), (1, 2)} or {(3), (2, 1)}

L(n, n) всегда равно 1, поскольку, например, разбиение множества {1, 2, 3} на 3 непустых подмножества приводит к подмножествам длины 1.

{(1), (2), (3)}

При использовании обозначения Карамата — Кнута для чисел Стирлинга было предложено использовать следующее альтернативное обозначение чисел Лаха:

[math]\displaystyle{ L(n,k)=\left\lfloor\begin{matrix} n \\ k \end{matrix}\right\rfloor. }[/math]

Возрастающие и убывающие факториалы

Пусть [math]\displaystyle{ x^{(n)} }[/math] обозначает возрастающий факториал [math]\displaystyle{ x(x+1)(x+2) \cdots (x+n-1) }[/math], а [math]\displaystyle{ (x)_n }[/math] — убывающий факториал [math]\displaystyle{ x(x-1)(x-2) \cdots (x-n+1) }[/math].

Тогда [math]\displaystyle{ x^{(n)} = \sum_{k=1}^n L(n,k) (x)_k }[/math] and [math]\displaystyle{ (x)_n = \sum_{k=1}^n (-1)^{n-k} L(n,k)x^{(k)}. }[/math]

Например, [math]\displaystyle{ x(x+1)(x+2) = {\color{red}6}x + {\color{red}6}x(x-1) + {\color{red}1}x(x-1)(x-2). }[/math]

Сравните с третьей строкой таблицы значений.

Тождества и связи

[math]\displaystyle{ L(n,k) = {n-1 \choose k-1} \frac{n!}{k!} = {n \choose k} \frac{(n-1)!}{(k-1)!} = {n \choose k} {n-1 \choose k-1} (n-k)! }[/math]

[math]\displaystyle{ L(n,k) = \frac{n!(n-1)!}{k!(k-1)!}\cdot\frac{1}{(n-k)!} = \left (\frac{n!}{k!} \right )^2\frac{k}{n(n-k)!} }[/math]

[math]\displaystyle{ L(n,k+1) = \frac{n-k}{k(k+1)} L(n,k). }[/math]

[math]\displaystyle{ L(n,k) = \sum_{j} \left[{n\atop j}\right] \left\{{j\atop k}\right\}, }[/math] где [math]\displaystyle{ \left[{n\atop j}\right] }[/math] — числа Стирлинга первого рода, а [math]\displaystyle{ \left\{{j\atop k}\right\} }[/math] — числа Стирлинга второго рода. Если принять, что [math]\displaystyle{ L(0,0)=1 }[/math] и [math]\displaystyle{ L(n , k )=0 }[/math] при [math]\displaystyle{ k\gt n }[/math].

[math]\displaystyle{ L(n,1) = n! }[/math]

[math]\displaystyle{ L(n,2) = (n-1)n!/2 }[/math]

[math]\displaystyle{ L(n,3) = (n-2)(n-1)n!/12 }[/math]

[math]\displaystyle{ L(n,n-1) = n(n-1) }[/math]

[math]\displaystyle{ L(n,n) = 1 }[/math]

[math]\displaystyle{ \sum_{n\geq k}L(n,k)\frac{x^n}{n!}= \frac{1}{k!}\left( \frac{x}{1-x} \right)^k }[/math]

Таблица значений

Таблица значений чисел Лаха:

[math]\displaystyle{ _n\!\!\diagdown\!\!^k }[/math]	1	2	3	4	5	6	7	8	9	10	11	12
1	1
2	2	1
3	6	6	1
4	24	36	12	1
5	120	240	120	20	1
6	720	1800	1200	300	30	1
7	5040	15120	12600	4200	630	42	1
8	40320	141120	141120	58800	11760	1176	56	1
9	362880	1451520	1693440	846720	211680	28224	2016	72	1
10	3628800	16329600	21772800	12700800	3810240	635040	60480	3240	90	1
11	39916800	199584000	299376000	199584000	69854400	13970880	1663200	11880	4950	110	1
12	479001600	2634508800	4390848000	3293136000	1317254400	307359360	43908480	3920400	217800	7260	132	1

См. также

• Числа Стирлинга
• Матрица Паскаля