Частичный след

Слева полная матрица плотности [math]\displaystyle{ \rho_{AB} }[/math] двухчастичной системы. Справа редуцированная матрица плотности [math]\displaystyle{ \rho_{A} }[/math] первой частицы полученная как частичный след для второй частицы.

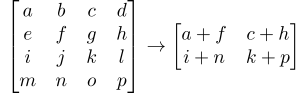
В линейной алгебре частичный след обобщает понятие след матрицы. Cлед линейного оператора является скаляром, тогда как частичный след сам является линейным оператором. Частичный след применяется в квантовой информатике и теории декогеренции.

Определение

Для любого пространства [math]\displaystyle{ A }[/math], обозначим пространство линейных операторов на [math]\displaystyle{ A }[/math] нем как [math]\displaystyle{ L(A) }[/math]. Пусть [math]\displaystyle{ V }[/math], [math]\displaystyle{ W }[/math] являются конечномерными векторными пространствами над полем с размерностями [math]\displaystyle{ m }[/math] и [math]\displaystyle{ n }[/math] соответственно. Пусть базисами в V иW будут соответственно [math]\displaystyle{ v_1, \ldots, v_m }[/math], и [math]\displaystyle{ w_1, \ldots, w_n }[/math].

Частичный след [math]\displaystyle{ \operatorname{Tr}_W }[/math] для пространства [math]\displaystyle{ W }[/math], это отображение [math]\displaystyle{ \{a_{k \ell, i j}\} = A \in \operatorname{L}(V \otimes W) \mapsto \{b_{k, i}\} = \operatorname{Tr}_W (A) \in \operatorname{L}(V) }[/math] заданное соотношением [math]\displaystyle{ b_{k, i} = \sum_{j=1}^n a_{k j, i j}. }[/math]

Линейный оператор заданный таким образом не зависит от выбора базиса [math]\displaystyle{ v_1, \ldots, v_m }[/math], и [math]\displaystyle{ w_1, \ldots, w_n }[/math].

Частичный след как квантовая операция

Рассмотрим двухчастичные состояния. Чистые вектора-состояния принадлежат гильбертову пространству [math]\displaystyle{ H_A \otimes H_B }[/math], а матрицы плотности, соответственно, [math]\displaystyle{ H_A \otimes H_B \otimes H^*_A \otimes H^*_B }[/math]. Рассмотрим матрицу плотности [math]\displaystyle{ \rho_{AB} \in H_A \otimes H_B \otimes H^*_A \otimes H^*_B }[/math].

[math]\displaystyle{ \{ {\left|{i}\right\rangle}_A \} }[/math] и [math]\displaystyle{ \{ {\left|{i}\right\rangle}_B \} }[/math] — базисы пространств [math]\displaystyle{ H_A }[/math] и [math]\displaystyle{ H_B }[/math] соответственно.

Тогда подсистема [math]\displaystyle{ A }[/math] описывается матрицей плотности [math]\displaystyle{ \rho_A = \operatorname{Tr}_B(\rho_{AB})=\sum_{{\left|{i}\right\rangle}_B} { {\left\langle{i}\right|}_B \rho_{AB}{\left|{i}\right\rangle}_B } }[/math]

Литература

• Д. А. Кронберг, Ю. И. Ожигов, А. Ю. Чернявский (2012). «Алгебраический аппарат квантовой информатики».