Формула поворота Родрига

Формула поворота Родрига — формула, связывающая два вектора с общим началом, один из которых получен поворотом другого на известный угол вокруг оси, проходящей через их общее начало:

[math]\displaystyle{ \vec{R}_2 - \tan(\chi/2) [\vec{e} \times \vec{R}_2] = \vec{R}_1 + \tan(\chi/2) [\vec{e} \times \vec{R}_1] }[/math]

где [math]\displaystyle{ \vec{R}_1 }[/math] — исходный вектор, [math]\displaystyle{ \vec{R}_2 }[/math] — результирующий вектор, [math]\displaystyle{ \vec{e} }[/math] — единичный вектор оси поворота, [math]\displaystyle{ \chi }[/math] — угол поворота. Также формула может быть записана в виде:

[math]\displaystyle{ \vec{R}_2 = (\vec{e} \cdot \vec{R}_1)(1-\cos\chi) \vec{e} + (\vec{e} \times \vec{R}_1)\sin\chi + \vec{R}_1 \cdot \cos \chi }[/math]

Лежит в основе векторной теории конечных поворотов и сложения вращений. Получена О. Родригом в 1840 г.

Вывод

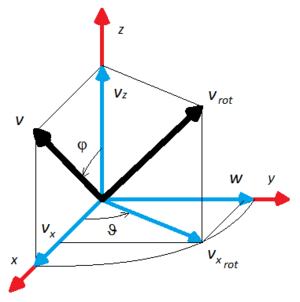
Без потери общности, направим ось [math]\displaystyle{ \vec{z} }[/math] вдоль единичного вектора [math]\displaystyle{ \vec{e} }[/math], а вектор [math]\displaystyle{ \vec{R}_1 }[/math] — лежащим в плоскости OXZ, тогда:

[math]\displaystyle{ \vec{R}_{1x} = \vec{R}_1 - \vec{R}_{1z} }[/math]

[math]\displaystyle{ \vec{R}_{1y} = 0 }[/math]

[math]\displaystyle{ \vec{R}_{1z} = (\vec{e} \cdot \vec{R}_1) \vec{e} }[/math]

Откуда:

[math]\displaystyle{ \vec{R}_{1x} = \vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e} }[/math]

Положим вектор [math]\displaystyle{ \vec{w} }[/math], равный:

[math]\displaystyle{ \vec{w} = \vec{e}\times\vec{R}_1 }[/math]

Заметим, что:

[math]\displaystyle{ |\vec{w}| = |\vec{e} \times \vec{R}_1| = |\vec{e}| \, |\vec{R}_1| \sin \phi \ = |\vec{R}_1| \sin \phi }[/math]

[math]\displaystyle{ |\vec{R}_{1x}| = |\vec{R}_1| \cos(\pi/2-\phi) = |\vec{R}_1| \sin \phi. }[/math]

Тогда вектор [math]\displaystyle{ \vec{R}_{2x} }[/math] можно выразить через векторы [math]\displaystyle{ \vec{w} }[/math] и [math]\displaystyle{ \vec{R}_{1x} }[/math] и угол [math]\displaystyle{ \chi }[/math]:

[math]\displaystyle{ \vec{R}_{2x} = \vec{R}_{1x}\cos\chi + \vec{w}\sin\chi = (\vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e})\cos\chi + (\vec{e} \times \vec{R}_1)\sin\chi }[/math]

Результирующий вектор [math]\displaystyle{ \vec{R}_2 }[/math] выражается через векторы [math]\displaystyle{ \vec{R}_{2x} }[/math] и [math]\displaystyle{ \vec{R}_{1z} }[/math]:

[math]\displaystyle{ \vec{R}_2 = \vec{R}_{2x} + \vec{R}_{1z} = (\vec{R}_1 - (\vec{e} \cdot \vec{R}_1) \vec{e})\cos\chi + (\vec{e} \times \vec{R}_1)\sin\chi + (\vec{e} \cdot \vec{R}_1) \vec{e} }[/math]

Приведя подобные, получим формулу поворота Родрига:

[math]\displaystyle{ \vec{R}_2 = (\vec{e} \cdot \vec{R}_1)(1-\cos\chi) \vec{e} + (\vec{e} \times \vec{R}_1)\sin\chi + \vec{R}_1 \cdot \cos \chi }[/math]

В матричной форме

Векторное умножение на вектор k можно представить в виде умножения на матрицу K:

[math]\displaystyle{ \mathbf{k}\times\mathbf{v} = \begin{bmatrix} (\mathbf{k}\times\mathbf{v})_x \\ (\mathbf{k}\times\mathbf{v})_y \\ (\mathbf{k}\times\mathbf{v})_z \end{bmatrix} = \begin{bmatrix} k_y v_z - k_z v_y \\ k_z v_x - k_x v_z \\ k_x v_y - k_y v_x \end{bmatrix} = \begin{bmatrix} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x & 0 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} = \mathbf{K}\mathbf{v}\,. }[/math]

Вектор v при повороте вокруг единичного вектора k перейдет в вектор

[math]\displaystyle{ \mathbf{v}_{\mathrm{rot}} = \mathbf{v} + (\sin\theta) \mathbf{K}\mathbf{v} + (1-\cos\theta)\mathbf{K}^2\mathbf{v} = \mathbf{R}\mathbf{v} \,, }[/math]

где [math]\displaystyle{ \mathbf{K}(\mathbf{K}\mathbf{v}) = \mathbf{K}^2\mathbf{v} = \mathbf{k}\times(\mathbf{k}\times\mathbf{v}) \,. }[/math]

Таким образом получается, что матрица поворота вокруг единичного вектора k на угол [math]\displaystyle{ \theta }[/math]

[math]\displaystyle{ \mathbf{R} = \mathbf{I} + (\sin\theta) \mathbf{K} + (1-\cos\theta)\mathbf{K}^2 ~. }[/math]

где

[math]\displaystyle{ \mathbf{K}= \left[\begin{array}{ccc} 0 & -k_z & k_y \\ k_z & 0 & -k_x \\ -k_y & k_x & 0 \end{array}\right]~. }[/math]

Литература

• Лурье А. И.  Аналитическая механика. — М.: Физматгиз, 1961. — 824 с. — С. 101—103.
• Rodrigues O.  Des lois géométriques qui régissent les déplacements d’une système solide dans l’espace et de la variation des coordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire // Liouvillés Journ. Math.. — 1840. — Vol. 5. — P. 380—440.