Точная раскраска

Пример точной раскраски с 7 цветами и 14 вершинами

Точная раскраска — это раскраска вершин, в которой каждая пара цветов появляется ровно один раз на паре смежных вершин, разбиение вершин графа на непересекающиеся независимые множества. Таким образом, для каждой пары различных независимых множеств в разбиении существует только одно ребро, концы которого принадлежат обоим множествам.

Полные графы, расщепления и эйлеровы циклы

Точная раскраска полного графа K₆

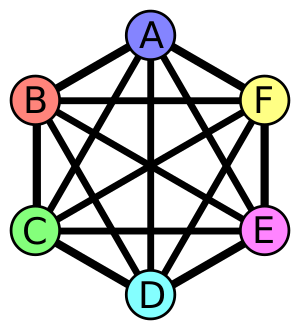
Любой полный граф K_n с n вершинами имеет точную раскраску n цветами, которая получается путём задания каждой вершине отдельного цвета. Также любой граф с n-цветной точной раскраской можно получить при помощи расщепления полного графа путём распадения на частицы каждой вершины на независимое множество и переключения каждого ребра, смежного вершине, ровно на одного члена соответствующего независимого множества

Если k нечётно, путь или цикл с [math]\displaystyle{ \tbinom{k}{2} }[/math] рёбрами имеет точную раскраску, которая получается с помощью формирования точной раскраски полного графа K_k и нахождения затем эйлерова цикла этого полного графа. Например, путь с тремя рёбрами имеет полную 3-раскраску.

Связанные виды раскрасок

Точные раскраски тесно связаны с гармоническими раскрасками (каждая пара цветов появляется максимум один раз) и полными раскрасками, поэтому точная раскраска одновременно гармоническая и полная. Граф G с n вершинами и m рёбрами имеет гармоничную k-раскраску тогда и только тогда, когда [math]\displaystyle{ m\leqslant\tbinom{k}{2} }[/math] и граф, образованный из G путём добавления [math]\displaystyle{ \tbinom{k}{2}-m }[/math] изолированных рёбер имеет точную раскраску. Граф G с теми же параметрами имеет полную k-раскраску тогда и только тогда, когда [math]\displaystyle{ m\geqslant\tbinom{k}{2} }[/math] и существует подграф H графа G с точной k-раскраской, в которой каждое ребро графа [math]\displaystyle{ G - H }[/math] имеет концы с разными цветами. Необходимость условия на рёбра [math]\displaystyle{ G - H }[/math] показывается примером цикла с четырьмя вершинами, который имеет подграф с точной 3-раскраской (путь из трёх рёбер), но сам полной 3-раскраски не имеет.

Вычислительная сложность

Задача определения, имеет ли заданный граф точную раскраску, NP-полна даже для случая, когда граф является деревом. Однако задача может быть решена за полиномиальное время для деревьев ограниченной степени.

Литература

• Keith Edwards. Detachments of complete graphs // Combinatorics, Probability and Computing. — 2005. — Т. 14, вып. 3. — С. 275–310. — doi:10.1017/S0963548304006558.
• Keith Edwards. Achromatic number of fragmentable graphs // Journal of Graph Theory. — 2010. — Т. 65, вып. 2. — С. 94–114. — doi:10.1002/jgt.20468.
• Keith Edwards, Colin McDiarmid. The complexity of harmonious colouring for trees // Discrete Applied Mathematics. — 1995. — Т. 57, вып. 2—3. — С. 133–144. — doi:10.1016/0166-218X(94)00100-R.
• Keith Edwards. The harmonious chromatic number of bounded degree trees // Combinatorics, Probability and Computing. — 1996. — Т. 5, вып. 1. — С. 15–28. — doi:10.1017/S0963548300001802.