Теорема о неявной функции

Теорема о неявной функции — общее название для теорем, гарантирующих локальное существование и описывающих свойства неявной функции, то есть функции

[math]\displaystyle{ y=f(x) }[/math], [math]\displaystyle{ f:X\to Y }[/math],

заданной уравнением

[math]\displaystyle{ F(x,y)=z_0 }[/math], [math]\displaystyle{ F:X\times Y\to Z }[/math],

где значение [math]\displaystyle{ z_0\in Z }[/math] фиксировано.

Одномерный случай

Простейшая теорема о неявной функции состоит в следующем.

Если функция [math]\displaystyle{ F:\R\times\R\to\R }[/math]

• непрерывна в некоторой окрестности точки [math]\displaystyle{ (x_0,y_0) }[/math]
• [math]\displaystyle{ F(x_0,y_0)=0 }[/math] и
• при фиксированном [math]\displaystyle{ x }[/math] функция [math]\displaystyle{ F(x,y) }[/math] строго монотонна по [math]\displaystyle{ y }[/math] в данной окрестности,

тогда найдётся такой двумерный промежуток [math]\displaystyle{ I=I_x \times I_y }[/math], являющийся окрестностью точки [math]\displaystyle{ (x_0,y_0) }[/math], и такая непрерывная функция [math]\displaystyle{ f:I_x\to I_y }[/math], что для любой точки [math]\displaystyle{ (x,y) \in I }[/math]

[math]\displaystyle{ F(x,y) = 0 \Leftrightarrow y = f(x) }[/math]

Обычно дополнительно предполагается, что функция [math]\displaystyle{ F }[/math] является непрерывно дифференцируемой в окрестности точки [math]\displaystyle{ (x_0,y_0) }[/math]. В том случае строгая монотонность следует из условия [math]\displaystyle{ F_y'(x_0,y_0)\ne 0 }[/math], где [math]\displaystyle{ F_y' }[/math] обозначает частную производную [math]\displaystyle{ F }[/math] по [math]\displaystyle{ y }[/math]. Более того, в этом случае функция [math]\displaystyle{ f }[/math] также является непрерывно дифференцируемой, и её производная может быть вычислена по формуле

[math]\displaystyle{ f'(x) = - \frac{F_x'(x, f(x))}{F_y'(x, f(x))}. }[/math]

Пример

Иллюстрация примера.

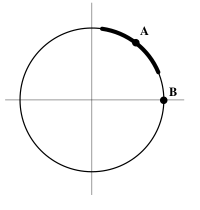
Рассмотрим функцию [math]\displaystyle{ F(x,y)=x^2 + y^2 - 1 }[/math] и соответствующее уравнение

[math]\displaystyle{ F(x,y)=x^2 + y^2 - 1 = 0 }[/math],

которое задает на плоскости единичную окружность. Невозможно представить всю окружность в виде графика какой-либо функции [math]\displaystyle{ y=f(x) }[/math]. Действительно, каждому значению [math]\displaystyle{ x \in (-1,1) }[/math] отвечает два разных значения [math]\displaystyle{ \pm\sqrt{1-x^2} }[/math]. Однако можно представить часть окружности в виде графика. Например, график функции [math]\displaystyle{ g_1(x) = \sqrt{1-x^2} }[/math], определенной на отрезке [math]\displaystyle{ x \in [-1,1] }[/math], задаёт верхнюю половину окружности, а график функции [math]\displaystyle{ g_2(x) = -g_1(x) }[/math] задаёт её нижнюю половину.

Теорема о неявной функции имеет локальный характер и говорит о том, что в малой окрестности любой точки окружности, в которой выполнено условие [math]\displaystyle{ F_y(x,y) \neq 0 }[/math] часть окружности, находящаяся в этой окрестности, представима в виде графика гладкой функции. Это условие выполнено, например, в точке [math]\displaystyle{ A }[/math] на рисунке. Существуют лишь две точки окружности ([math]\displaystyle{ B }[/math] и диаметрально противоположная ей точка), в которых условие [math]\displaystyle{ F_y(x,y) \neq 0 }[/math] нарушено. Очевидно, что в сколь угодно малой окрестности каждой из этих точек часть окружности не представима в виде графика какой-либо функции [math]\displaystyle{ y=f(x) }[/math].

Многомерный случай

Пусть [math]\displaystyle{ \R^n }[/math] и [math]\displaystyle{ \R^m }[/math] — пространства с координатами [math]\displaystyle{ x=(x_1,\dots,x_n) }[/math] и [math]\displaystyle{ y=(y_1,\dots,y_m) }[/math], соответственно. Рассмотрим отображение [math]\displaystyle{ F=(F_1,\ldots,F_m), }[/math] [math]\displaystyle{ F_i = F_i(x,y), }[/math] которое отображает некоторую окрестность [math]\displaystyle{ W }[/math] точки [math]\displaystyle{ (x_0,y_0)\in\R^n\times\R^m }[/math] в пространство [math]\displaystyle{ \R^m }[/math].

Предположим, что отображение [math]\displaystyle{ F }[/math] удовлетворяет следующим условиямː

• [math]\displaystyle{ F \in C^{k}(W), }[/math] [math]\displaystyle{ k \geq 1, }[/math] то есть [math]\displaystyle{ F }[/math] является [math]\displaystyle{ k }[/math] раз непрерывно дифференцируемым в [math]\displaystyle{ W, }[/math]
• [math]\displaystyle{ F(x_0,y_0)=0, }[/math]
• якобиан отображения [math]\displaystyle{ y\mapsto F(x_0,y) }[/math] не равен нулю в точке [math]\displaystyle{ y_0, }[/math] то есть определитель матрицы [math]\displaystyle{ \frac{\partial F}{\partial y}(x_0,y_0) }[/math] не равен нулю.

Тогда существуют окрестности [math]\displaystyle{ U }[/math] и [math]\displaystyle{ V }[/math] точек [math]\displaystyle{ x_0 }[/math] и [math]\displaystyle{ y_0 }[/math] в пространствах [math]\displaystyle{ \R^n }[/math] и [math]\displaystyle{ \R^m }[/math] соответственно, причём [math]\displaystyle{ U\times V\subset W }[/math], и отображение [math]\displaystyle{ f : U \to V, }[/math] [math]\displaystyle{ f \in C^{k}(U), }[/math] такие, что

[math]\displaystyle{ F(x,y) = 0 \Leftrightarrow y = f(x) }[/math]

для всех [math]\displaystyle{ x \in U }[/math] и [math]\displaystyle{ y \in V }[/math]. Отображение [math]\displaystyle{ f }[/math] определено однозначно.

Естественным обобщением предыдущей теоремы на случай не гладких отображений является следующая теоремаː

Предположим, что отображение [math]\displaystyle{ F }[/math] удовлетворяет следующим условиямː

• [math]\displaystyle{ F }[/math] является непрерывным в [math]\displaystyle{ W, }[/math]
• [math]\displaystyle{ F(x_0,y_0)=0, }[/math]
• существуют окрестности [math]\displaystyle{ U }[/math] и [math]\displaystyle{ V }[/math] точек [math]\displaystyle{ x_0 }[/math] и [math]\displaystyle{ y_0 }[/math] в пространствах [math]\displaystyle{ \R^n }[/math] и [math]\displaystyle{ \R^m }[/math] соответственно, причём [math]\displaystyle{ U\times V\subset W }[/math], такие, что для каждого фиксированного [math]\displaystyle{ x \in U }[/math] отображение [math]\displaystyle{ y\mapsto F(x,y) }[/math] является взаимно однозначным в [math]\displaystyle{ V }[/math].

Тогда существует такое непрерывное отображение [math]\displaystyle{ f : U \to V }[/math], что

[math]\displaystyle{ F(x,y) = 0 \Leftrightarrow y = f(x) }[/math]

для всех [math]\displaystyle{ x \in U }[/math] и [math]\displaystyle{ y \in V }[/math].

См. также

• Теорема об обратной функции

Литература

• Зорич В. А. Математический анализ, Любое издание
• Ильин В. А., Позняк Э. Г. Основы математического анализа, 3 изд., ч. 1, М., 1971
• Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 5 изд., М., 1981
• Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 2 изд., М., 1965
• Никольский С. М. Курс математического анализа, 2 изд., т. 1—2, М., 1975
• Понтрягин Л. С. Обыкновенные дифференциальные уравнения, 4 изд., М., 1974 — § 33
• Шварц Л. Анализ, пер. с франц., т. 1, М., 1972