Теорема о вписанных окружностях
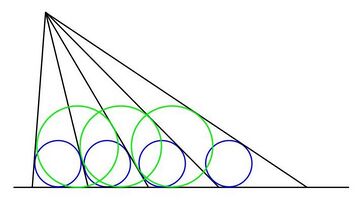
Теорема о вписанных окружностях берёт начало в японских сангаку и относится к следующему построению: серия лучей проводится из некой точки на заданную прямую так, что окружности, вписанные в получающиеся треугольники, образованные смежными лучами и прямой, одинаковы. На иллюстрации одинаковые синие окружности определяют угол между лучами, как описано выше.
Формулировка теоремы
Теорема утверждает, что при описанном выше построении окружности, вписанные в треугольники, образованными лучами через один (то есть полученные объединением двух соседних треугольников), через два и т. д., также равны. Случай соседних треугольников показан на рисунке зелёными окружностями: все они имеют одинаковые размеры.
Из факта, что утверждение теоремы не зависит от угла между начальным лучом и заданной прямой, можно сделать вывод, что теорема скорее относится к математическому анализу, а не геометрии, и должна иметь отношение к непрерывной масштабной функции, которая определяет расстояние между лучами. Фактически этой функцией является гиперболический синус.
Лемма
Теорема является прямым следствием следующей леммы.
Предположим, что n-й луч имеет угол [math]\displaystyle{ \gamma_n }[/math] к нормали для базовой прямой. Если [math]\displaystyle{ \gamma_n }[/math] параметризовано согласно равенству [math]\displaystyle{ \mathrm{tg}\,\gamma_n = \mathrm{sh}\,\theta_n }[/math], то значения [math]\displaystyle{ \theta_n = a + nb }[/math], где [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] являются вещественными константами, определяют последовательность лучей, которые удовлетворяют условиям вписанных окружностей (см. выше), и более того, любая последовательность лучей, удовлетворяющих этим условиям, может быть получена надлежащим выбором параметров [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math].
Доказательство леммы
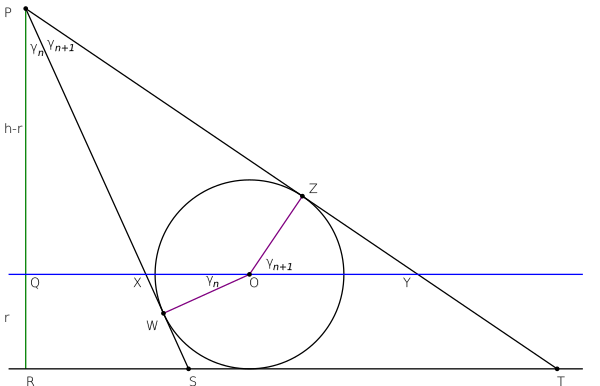
На рисунке прямые PS и PT являются смежными лучами, имеющими углы [math]\displaystyle{ \gamma_n }[/math] и [math]\displaystyle{ \gamma_{n+1} }[/math] с прямой PR, перпендикулярной базовой прямой RT.
Проведём прямую QY, параллельную базовой прямой, через центр O вписанной в треугольник [math]\displaystyle{ \triangle }[/math] PST окружности. Эта окружность касается лучей в точках W и Z. Отрезок PQ имеет длину [math]\displaystyle{ h-r }[/math], а отрезок QR имеет длину [math]\displaystyle{ r }[/math], что равно радиусу вписанной окружности.
Тогда [math]\displaystyle{ \triangle }[/math] OWX подобен [math]\displaystyle{ \triangle }[/math] PQX, [math]\displaystyle{ \triangle }[/math] OZY подобен [math]\displaystyle{ \triangle }[/math] PQY, а из XY = XO + OY мы получаем
- [math]\displaystyle{ (h-r) (\mathrm{tg}\,\gamma_{n+1} - \mathrm{tg}\,\gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ). }[/math]
Это отношение на множестве углов [math]\displaystyle{ \{ \gamma_m \} }[/math] выражает условие равенства вписанных окружностей.
Для доказательства леммы положим [math]\displaystyle{ \mathrm{tg}\,\gamma_n = \mathrm{sh}\,(a+nb) }[/math]. Это выражение можно преобразовать в [math]\displaystyle{ \sec \gamma_n = \mathrm{ch}\,(a+nb) }[/math].
Используя равенство [math]\displaystyle{ a+(n+1)b = (a+nb)+b }[/math], мы применяем дополнительные правила для [math]\displaystyle{ \mathrm{sh}\, }[/math] и [math]\displaystyle{ \mathrm{ch}\, }[/math] и проверяем, что отношение равенства окружностей удовлетворяется выражением
- [math]\displaystyle{ \frac {r}{h-r} = \mathrm{th}\, \tfrac{b}{2}. }[/math]
Мы получили выражение для параметра [math]\displaystyle{ b }[/math] в терминах геометрических величин [math]\displaystyle{ h }[/math] и [math]\displaystyle{ r }[/math]. Далее, определяя [math]\displaystyle{ b }[/math], мы получаем выражение для радиусов [math]\displaystyle{ r_N }[/math] вписанных окружностей, образованных выбором каждого N-го луча в качестве сторон треугольника:
- [math]\displaystyle{ \frac {r_N}{h-r_N} = \mathrm{th}\, \tfrac{Nb}{2}. }[/math]
См. также
Литература
- Tabov J. A note on the five-circle theorem // Mathematics Magazine. — 1989. — Т. 63. — № 2. — С. 92—94.