Тематическое моделирование

Построение тематической модели документа: : [math]\displaystyle{ p(w|t) }[/math] — матрица искомых условных распределений слов по темам : [math]\displaystyle{ p(t|d) }[/math] матрица искомых условных распределений тем по документам : [math]\displaystyle{ d }[/math] — документ : [math]\displaystyle{ w }[/math] — слово : [math]\displaystyle{ d, w }[/math] — наблюдаемые переменные : [math]\displaystyle{ t }[/math] — тема (скрытая переменная)

Тематическое моделирование — способ построения модели коллекции текстовых документов, которая определяет, к каким темам относится каждый из документов.

Тематическая модель (англ. topic model) коллекции текстовых документов определяет, к каким темам относится каждый документ и какие слова (термины) образуют каждую тему.

Переход из пространства терминов в пространство найденных тематик помогает разрешать синонимию и полисемию терминов, а также эффективнее решать такие задачи, как тематический поиск, классификация, суммаризация и аннотация коллекций документов и новостных потоков.

Тематическое моделирование как вид статистических моделей для нахождения скрытых тем, встреченных в коллекции документов, нашло своё применение в таких областях, как машинное обучение и обработка естественного языка. Исследователи используют различные тематические модели для анализа текстов, текстовых архивов документов, для анализа изменения тем в наборах документов. Интуитивно понимая, что документ относится к определённой теме, в документах, посвящённых одной теме, можно встретить некоторые слова чаще других. Например: «собака» и «кость» встречаются чаще в документах про собак, «кошки» и «молоко» будут встречаться в документах о котятах, предлоги «и» и «в» будут встречаться в обеих тематиках. Обычно документ касается нескольких тем в разных пропорциях, таким образом, документ в котором 10 % темы составляют кошки, а 90 % темы — собаки, можно предположить, что слов про собак в 9 раз больше. Тематическое моделирование отражает эту интуицию в математической структуре, которая позволяет на основании изучения коллекции документов и исследования частотных характеристик слов в каждом документе сделать вывод, что каждый документ — это некоторый баланс тем.

Наибольшее применение в современных приложениях находят подходы, основанные на Байесовских сетях — вероятностных моделях на ориентированных графах. Вероятностные тематические модели — это относительно молодая область исследований в теории самообучения. Одним из первых был предложен вероятностный латентно-семантический анализ (PLSA), основанный на принципе максимума правдоподобия, как альтернатива классическим методам кластеризации, основанным на вычислении функций расстояния. Вслед за PLSA был предложен метод латентного размещения Дирихле и его многочисленные обобщения.

Вероятностные тематические модели осуществляют «мягкую» кластеризацию, позволяя документу или термину относиться сразу к нескольким темам с различными вероятностями. Вероятностные тематические модели описывает каждую тему дискретным распределением на множестве терминов, каждый документ — дискретным распределением на множестве тем. Предполагается, что коллекция документов — это последовательность терминов, выбранных случайно и независимо из смеси таких распределений, и ставится задача восстановления компонентов смеси по выборке.

Хотя тематическое моделирование традиционно описывалось и применялось в обработке естественного языка, оно нашло своё применение и в других областях, например, таких как биоинформатика.

История

Первое описание тематического моделирования появилось в работе Рагавана, Пападимитриу, Томаки и Вемполы 1998 года. Томас Хофманн в 1999 году предложил вероятностное скрытое семантическое индексирование (PLSI). Одна из самых распространенных тематических моделей — это латентное размещение Дирихле (LDA), эта модель является обобщением вероятностного семантического индексирования и разработана Дэвидом Блейем (англ. David Blei), Эндрю Ыном и Майклом Джорданом (англ. Michael I. Jordan) в 2002 году. Другие тематические модели как правило являются расширением LDA, например, размещение патинко улучшает LDA за счёт введения дополнительных корреляционных коэффициентов для каждого слова, которое составляет тему.

Тематические исследования

Тэмплтон сделал обзор работ по тематическому моделированию в гуманитарных науках, сгруппированных по синхронному и диахроническому подходу. Синхронные подходы выделяют темы в некоторый момент времени, например, Джокерс с помощью тематической модели исследовал, о чём писали блогеры в День Цифровых Гуманитарных наук в 2010 году.

Диахронические подходы, включая определение Блока и Ньюмана о временной динамике тем в Пенсильванской газете 1728—1800 года. Грифитс и Стейверс использовали тематическое моделирование для обзоров журнала PNAS, определяли изменения популярности тем с 1991 по 2001 год. Блевин создал тематическую модель дневника Марты Балладс. Мимно использовал тематическое моделирование для анализа 24 журналов по классической филологии и археологии за 150 лет, чтобы определить изменения популярности тем и узнать, насколько сильно изменились журналы за это время.

Алгоритмы тематического моделирования

В работе Дэвида Блея «Введение в тематическое моделирование» рассмотрен наиболее популярный алгоритм Латентное размещение Дирихле. На практике исследователи используют одну из эвристик метода максимального правдоподобия, методы сингулярного разложения (SVD), метод моментов, алгоритм, основанный на неотрицательной матрице факторизации (NMF), вероятностные тематические модели, вероятностный латентно-семантический анализ, латентное размещение Дирихле. В работе Воронцова К. В. рассмотрены вариации основных алгоритмов тематического моделирования: робастная тематическая модель, тематические модели классификации, динамические тематические модели, иерархические тематические модели, многоязычные тематические модели, модели текста как последовательности слов, многомодальные тематические модели .

Вероятностные тематические модели основаны на следующих предположениях :

• Порядок документов в коллекции не имеет значения
• Порядок слов в документе не имеет значения, документ — мешок слов
• Слова, встречающиеся часто в большинстве документов, не важны для определения тематики
• Коллекцию документов можно представить как выборку пар документ-слово [math]\displaystyle{ (d, w) }[/math] , [math]\displaystyle{ d \in D }[/math], [math]\displaystyle{ w \in \mathit{W}_d }[/math]
• Каждая тема [math]\displaystyle{ t \in T }[/math] описывается неизвестным распределением [math]\displaystyle{ p(\mathit{W}|t) }[/math] на множестве слов [math]\displaystyle{ w \in \mathit{W} }[/math]
• Каждый документ [math]\displaystyle{ d \in D }[/math] описывается неизвестным распределением [math]\displaystyle{ p(t|d) }[/math] на множестве тем [math]\displaystyle{ t \in T }[/math]
• Гипотеза условной независимости [math]\displaystyle{ p(w|t,d) = p (w|t) }[/math]

Построить тематическую модель — значит, найти матрицы [math]\displaystyle{ \Phi = ||p(w|t)|| }[/math] и [math]\displaystyle{ \Theta = ||p(t|d)|| }[/math] по коллекции [math]\displaystyle{ \mathit{D} }[/math] В более сложных вероятностных тематических моделях некоторые из этих предположений заменяются более реалистичными.

Вероятностный латентно-семантический анализ

Вероятностный латентно-семантический анализ (PLSA). [math]\displaystyle{ d }[/math] — документ, [math]\displaystyle{ w }[/math] — слово, [math]\displaystyle{ d, w }[/math] — наблюдаемые переменные, [math]\displaystyle{ t }[/math] — тема (скрытая переменная), [math]\displaystyle{ p(d) }[/math] — априорное распределение на множестве документов, [math]\displaystyle{ p(w|t), p(t|d) }[/math] — искомые условные распределения, [math]\displaystyle{ D }[/math] — коллекция документов, [math]\displaystyle{ N }[/math] — длина документа в словах

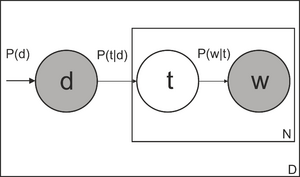
Вероятностный латентно-семантический анализ (PLSA) предложен Томасом Хофманном в 1999 году. Вероятностная модель появления пары «документ-слово» может быть записана тремя эквивалентными способами:

[math]\displaystyle{ p(d,w) = \sum_{t\in T} p(t) p(w|t) p(d|t) = \sum_{t\in T} p(d) p(w|t) p(t|d) = \sum_{t\in T} p(w) p(t|w) p(d|t) }[/math]

где [math]\displaystyle{ T }[/math] — множество тем;

[math]\displaystyle{ p(t) }[/math] — неизвестное априорное распределение тем во всей коллекции;

[math]\displaystyle{ p(d) }[/math] — априорное распределение на множестве документов, эмпирическая оценка [math]\displaystyle{ p(d) = n_d/n }[/math] , где [math]\displaystyle{ n = \sum_d n_d }[/math] — суммарная длина всех документов;

[math]\displaystyle{ p(w) }[/math] — априорное распределение на множестве слов, эмпирическая оценка [math]\displaystyle{ p(w) = n_w/n }[/math], где [math]\displaystyle{ n_w }[/math] — число вхождений слова [math]\displaystyle{ w }[/math] во все документы;

Искомые условные распределения [math]\displaystyle{ p(w|t), p(t|d) }[/math] выражаются через [math]\displaystyle{ p(t|w), p(d|t) }[/math] по формуле Байеса:

[math]\displaystyle{ p(w|t) = \frac{p(t|w)p(w)}{\sum_{w'} p(t|w')p(w')};\qquad p(t|d) = \frac{p(d|t)p(t)}{\sum_{t'} p(d|t')p(t')}. }[/math]

Для идентификации параметров тематической модели по коллекции документов применяется принцип максимума правдоподобия, который приводит к задаче максимизации функционала

[math]\displaystyle{ \sum_{d\in D} \sum_{w\in d} n_{dw}\ln \sum_{t\in \Tau} \varphi_{wt} \theta_{td} \to \max_{\Phi,\Theta} , }[/math]

при ограничениях нормировки

[math]\displaystyle{ \sum_w p(w|t) = 1,\; \sum_t p(t|d) = 1,\; \sum_t p(t) = 1, }[/math]

где [math]\displaystyle{ n_{dw} }[/math] — число вхождений слова [math]\displaystyle{ w }[/math] в документ [math]\displaystyle{ d }[/math]. Для решения данной оптимизационной задачи обычно применяется EM-алгоритм.

Основные недостатки PLSA:

• Число параметров растёт линейно по числу документов в коллекции, что может приводить к переобучению модели.
• При добавлении нового документа [math]\displaystyle{ d }[/math] в коллекцию распределение [math]\displaystyle{ p(t|d) }[/math] невозможно вычислить по тем же формулам, что и для остальных документов, не перестраивая всю модель заново.

Латентное размещение Дирихле

Латентное размещение Дирихле LDA. :[math]\displaystyle{ w }[/math] — слово (наблюдаемая переменная) :[math]\displaystyle{ t }[/math] — тема (скрытая переменная) :[math]\displaystyle{ D }[/math] — коллекция документов :[math]\displaystyle{ N }[/math] — длина документа в словах :[math]\displaystyle{ K }[/math] — количество тем в коллекции :[math]\displaystyle{ \theta }[/math] — распределение тем в документе :[math]\displaystyle{ \phi }[/math] — распределение слов в теме

Метод латентного размещения Дирихле (LDA) предложен Дэвидом Блеем в 2003 году.

В этом методе устранены основные недостатки PLSA.

Метод LDA основан на той же вероятностной модели

[math]\displaystyle{ p(d,w) = \sum_{t\in T} p(d) p(w|t) p(t|d), }[/math]

при дополнительных предположениях:

• вектора документов [math]\displaystyle{ \theta_d = \bigl(p(t|d): t\in T\bigr) }[/math] порождаются одним и тем же вероятностным распределением на нормированных [math]\displaystyle{ |T| }[/math]-мерных векторах; это распределение удобно взять из параметрического семейства распределений Дирихле [math]\displaystyle{ \mathrm{Dir}(\theta,\alpha),\; \alpha\in\mathbb{R}^{|T|} }[/math];
• вектора тем [math]\displaystyle{ \phi_t = \bigl(p(w|t): w\in W\bigr) }[/math] порождаются одним и тем же вероятностным распределением на нормированных векторах размерности [math]\displaystyle{ |W| }[/math]; это распределение удобно взять из параметрического семейства распределений Дирихле [math]\displaystyle{ \mathrm{Dir}(\theta,\beta),\; \beta\in\mathbb{R}^{|W|} }[/math].

Для идентификации параметров модели LDA по коллекции документов применяется семплирование Гиббса, вариационный байесовский вывод или метод распространения ожидания (Expectation propagation).

См. также

• Explicit semantic analysis
• Иерархический процесс Дирихле

Литература

• Коршунов Антон, Гомзин Андрей. Тематическое моделирование текстов на естественном языке // Труды Института системного программирования РАН : журнал. — 2012.
• Воронцов К.В. Вероятностное тематическое моделирование // www.machinelearning.ru : web. — 2013.
• Воронцов К.В., Потапенко А.А. Регуляризация, робастность и разреженность вероятностных тематических моделей // Компьютерные исследования и моделирование : журнал. — 2012. — С. 693-706.
• Воронцов К.В. Аддитивная регуляризация вероятностных тематических моделей Презентация // www.machinelearning.ru : web. — 2013.
• Воронцов К.В. Вероятностные тематические модели коллекции текстовых документов Презентация // www.machinelearning.ru : web. — 2013.
• Марк Стейверс, Tom Griffiths. Вероятностная тематическая модель. // Справочник скрытого семантического анализа / T. Landauer, D. McNamara, S. Dennis, W. Kintsch. — Psychology Press, 2007. — ISBN 978-0-8058-5418-3. Архивная копия от 24 июня 2013 на Wayback Machine
• Daud Ali, Li Juanzi, Zhou Lizhu, Muhammad Faqir. Knowledge discovery through directed probabilistic topic models: a survey. In Proceedings of Frontiers of Computer Science in China. // www.researchgate.net : web. — 2010.
• Christos Papadimitriou, Prabhakar Raghavan, Hisao Tamaki, Santosh Vempala. Latent Semantic Indexing: A probabilistic analysis // Proceedings of ACM PODS. — 1998. Архивировано 9 мая 2013 года.
• Thomas Hoffman. Probabilistic Latent Semantic Indexing // Proceedings of the Twenty-Second Annual International SIGIR Conference on Research and Development in Information Retrieval. — 1999. Архивировано 14 декабря 2010 года.
• David M. Blei, Andrew Y. Ng, Michael I. Jordan. Latent Dirichlet Allocation // Journal of Machine Learning Research. — 2003. Архивировано 1 мая 2012 года.
• David Blei. Introduction to Probabilistic Topic Models // Communications of the ACM. — 2012. — С. 77–84. Архивировано 15 февраля 2017 года.
• David Blei, J.D. Lafferty. Topic models : web. — 2009. Архивировано 31 мая 2013 года.
• David Blei, J.D. Lafferty. Introduction to Probabilistic Topic Models // Annals of Applied Statistics. — 2007. — С. 17–35. — doi:10.1214/07-AOAS114. Архивировано 15 февраля 2017 года.
• David Mimno. Computational Historiography: Data Mining in a Century of Classics Journals // Journal on Computing and Cultural Heritag : журнал. — 2012. — doi:10.1145/2160165.2160168.
• Matthew L. Jockers. Who's your DH Blog Mate: Match-Making the Day of DH Bloggers with Topic Modeling : web. — 2010.
• E. Микс. Понимание цифровых гуманитарных наук : web. — 2011.
• C. Тэмплтон. Тематическое моделирование в гуманитарных науках: обзор. // Maryland Institute for Technology in the Humanities Blog : web. — 2011.
• T. Гифитс, М. Стейверс. Нахождение научных тем // Proceedings of the National Academy of Sciences : журнал. — 2004. — doi:10.1073/pnas.0307752101. — PMID 14872004.
• T. Янг, A Торгет и Р. Mihalcea. Тематическое моделирование в исторических газетах // Proceedings of the 5th ACL-HLT Workshop on Language Technology for Cultural Heritage, Social Sciences, and Humanities. The Association for Computational Linguistics, Madison : журнал. — 2011. — С. 96–104. Архивировано 27 марта 2014 года.
• С. Блок. Делаем больше с оцифровкой- введение в тематическое моделирование в ранних американских источниках // Common-place The Interactive Journal of Early American Life : журнал. — 2006.
• Д. Ньюман, С. Блок. Вероятностное тематическое разложение в газетах 18 века // Journal of the American Society for Information Science and Technology : журнал. — 2006. — doi:10.1002/asi.20342.
• C. Блевин. Тематическое моделирование дневника Марты Баллардс // historying : web. — 2010.

Ссылки

• Лекция: Тематическое моделирование — К. В. Воронцов // Школа анализа данных (видео-лекции).
• Лекция 2: Тематическое моделирование — К. В. Воронцов // Школа анализа данных (видео-лекции).
• Тематическое моделирование (неопр.).
• Коллекции документов для тематического моделирования (неопр.).
• Полностью разреженные тематические модели (перевод) / Fully Sparse Topic Models (неопр.).
• Обзор по вероятностным тематическим моделям (неопр.).
• Тематические модели для коллекции текстов (неопр.).
• Байесовские методы машинного обучения (курс лекций, Д. П. Ветров, Д. А. Кропотов) (неопр.).
• Тепллтон, Клай Тематическое моделирование в гуманитарных науках. Общий обзор. (неопр.). Maryland Institute for Technology in the Humanities.
• Применение тематического моделирования для анализа новостей и ревю. Video of a Google Tech Talk presentation by Alice Oh on topic modeling with Latent Dirichlet allocation
• Моделирование науки: Динамическое тематическое моделирование научных исследований. Video of a Google Tech Talk presentation by David M. Blei
• Автоматизированная тематическая модель в политической науке. Video of a presentation by Brandon Stewart at the Tools for Text Workshop, 14 June 2010
• Лекция: Тематическое моделирование — Дэвид Блей 2009 г. Видео лекция Принстонский университет
• Регуляризация вероятностных тематических моделей для повышения интерпретируемости и определения числа тем Диалог 2014
• Parsimonious Topic Models with Salient Word Discovery

Программное обеспечение и программные библиотеки

• Малет (программа)
• Инструментарий Стэнфордского университета по тематическому моделированию
• GenSim — «тематическое моделирование для людей»
• LDA C# LDA in Infer.NET