Тела вращения
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости[1].
Примеры тел вращения
- Шар — образован полукругом, вращающимся вокруг диаметра разреза
- Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон
За площадь боковой поверхности цилиндра принимается площадь его развёртки:
- [math]\displaystyle{ S_{bok}=2 \pi r h }[/math].
- Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов
За площадь боковой поверхности конуса принимается площадь его развертки:
- [math]\displaystyle{ S_{bok}= \pi r l }[/math].
Площадь полной поверхности конуса:
- [math]\displaystyle{ S_{poln}= \pi r (r + l) }[/math].
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
Объём тел вращения
Вращение вокруг оси x

Объём тела, образуемого вращением вокруг оси [math]\displaystyle{ x }[/math] фигуры, ограниченной графиком функции [math]\displaystyle{ y=f(x) }[/math] на интервале [math]\displaystyle{ [a;b] }[/math], осью [math]\displaystyle{ x }[/math] и прямыми [math]\displaystyle{ x=a }[/math] и [math]\displaystyle{ x=b }[/math], равен:
- [math]\displaystyle{ V_x = \pi \int_{a}^{b} f^2(x) dx }[/math]
Вращение вокруг оси y
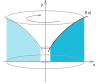
Объём тела, образуемого вращением вокруг оси [math]\displaystyle{ y }[/math] фигуры, ограниченной графиком функции [math]\displaystyle{ y=f(x) }[/math] на интервале [math]\displaystyle{ [a;b] }[/math], осью [math]\displaystyle{ x }[/math] и прямыми [math]\displaystyle{ x=a }[/math] и [math]\displaystyle{ x=b }[/math], равен:
- [math]\displaystyle{ V_y = 2\pi \int_{a}^{b} xf(x) dx }[/math]
Теорема Гульдина
Объём и площадь поверхности тел вращения можно также узнать при помощи теорем Гульдина-Паппа, которые связывают площадь или объём с центром масс фигуры.
- Первая теорема Гульдина-Паппа гласит:
|
Площадь поверхности, образуемой при вращении линии, лежащей в плоскости целиком по одну сторону от оси вращения, равна произведению длины линии на длину окружности, пробегаемой центром масс этой линии. |
- Вторая теорема Гульдина-Паппа гласит:
|
Объём тела, образуемого при вращении фигуры, лежащей в плоскости целиком по одну сторону от оси вращения, равен произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры. |
Литература
А. В. Погорелов. «Геометрия. 10-11 класс» § 21.Тела вращения. — 2011