Двойная звезда

Двойная звезда — это двойная звёздная система из гравитационно связанных звёзд, обращающихся по замкнутым орбитам вокруг общего центра масс. Двойные звёзды — весьма распространённые объекты. Примерно половина всех звёзд нашей Галактики принадлежит к двойным системам[1]. Звёзды, которые находятся на малом угловом расстоянии друг от друга на небесной сфере, но гравитационно не связаны, не относятся к двойным; они называются оптически-двойными.
Измерив период обращения и расстояние между звёздами, иногда можно определить массы компонентов системы. Этот метод практически не требует дополнительных модельных предположений, и поэтому является одним из главных методов определения масс в астрофизике. По этой причине двойные системы, компонентами которых являются чёрные дыры или нейтронные звёзды, представляют большой интерес для астрофизики.
Классификация
Физически двойные звезды можно разделить на два класса[2]:
- звёзды, между которыми обмен масс невозможен в принципе — разделённые двойные системы.
- звёзды, между которыми идёт, будет идти или шёл обмен массами — тесные двойные системы. Их в свою очередь можно разделить на:
- Полуразделённые, где только одна звезда заполняет свою полость Роша.
- Контактные, где обе звезды заполняют свои полости Роша.
Двойные системы также классифицируются по способу наблюдения, можно выделить визуальные, спектральные, затменные, астрометрические двойные системы.
Визуально-двойные звёзды
Двойные звезды, которые возможно увидеть раздельно (или, как говорят, которые могут быть разрешены), называются видимыми двойными, или визуально-двойными.
Возможность наблюдать звезду как визуально-двойную определяется разрешающей способностью телескопа, расстоянием до звёзд и расстоянием между ними. Таким образом, визуально-двойные звезды — это в основном звезды окрестностей Солнца с очень большим периодом обращения (следствие большого расстояния между компонентами). Из-за большого периода проследить орбиту двойной можно только по многочисленным наблюдениям на протяжении десятков лет. На сегодняшний день в каталогах WDS и CCDM свыше 78 000 и 110 000 объектов соответственно, и только у нескольких сотен из них можно вычислить орбиту. У менее чем сотни объектов орбита известна с достаточной точностью, чтобы получить массу компонентов.
При наблюдениях визуально-двойной звезды измеряют расстояние между компонентами и позиционный угол линии центров, иначе говоря, угол между направлением на северный полюс мира и направлением линии, соединяющей главную звезду с её спутником.
Спекл-интерферометрические двойные звезды
Спекл-интерферометрия наряду с адаптивной оптикой позволяет достичь дифракционного предела разрешения звёзд, что в свою очередь позволяет обнаруживать двойные звезды. Таким образом, спекл-интерферометрические двойные — это тоже визуально-двойные. Но если в классическом визуально-двойном методе необходимо получить два отдельных изображения, то в данном случае приходится анализировать спекл-интерферограммы[1].
Спекл-интерферометрия эффективна для двойных с периодом в несколько десятков лет[3].
Астрометрические двойные звёзды

В случае визуально-двойных звёзд мы видим перемещение по небу сразу двух объектов. Однако, если представить себе, что один из двух компонентов нам не виден по тем или иным причинам, то двойственность всё равно можно обнаружить по изменению положения на небе второго компонента. В таком случае говорят об астрометрически-двойных звёздах.
Если наличествуют высокоточные астрометрические наблюдения, то двойственность можно предположить, зафиксировав нелинейность движения: первую производную собственного движения и вторую[прояснить][4]. Астрометрические двойные звезды используются для измерения массы коричневых карликов разных спектральных классов[5].
Спектрально-двойные звёзды
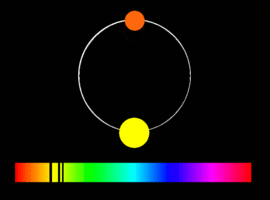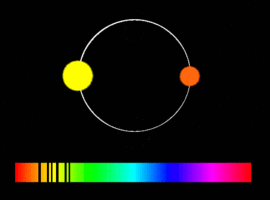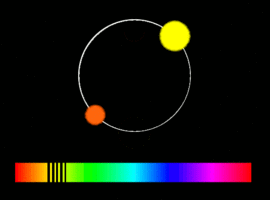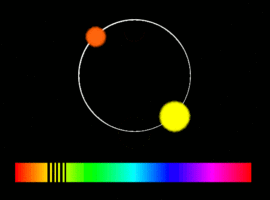
Спектрально-двойной называют звезду, двойственность которой обнаруживается при помощи спектральных наблюдений. Для этого её наблюдают в течение нескольких ночей. Если оказывается, что линии её спектра периодически смещаются со временем, то это означает, что скорость источника меняется. Этому может быть множество причин: переменность самой звезды, наличие у неё плотной расширяющейся оболочки, образовавшейся после вспышки сверхновой, и т. п.
Если получен спектр второй компоненты, который показывает аналогичные смещения, но в противофазе, то можно с уверенностью говорить, что перед нами двойная система. Если первая звезда к нам приближается и её линии сдвинуты в фиолетовую сторону спектра, то вторая — удаляется, и её линии сдвинуты в красную сторону, и наоборот.
Но если вторая звезда сильно уступает по яркости первой, то мы имеем шанс её не увидеть, и тогда нужно рассмотреть другие возможные варианты. Главный признак двойной звезды — периодичность изменения лучевых скоростей и большая разница между максимальной и минимальной скоростью. Но, строго говоря, не исключено, что обнаружена экзопланета. Чтобы это выяснить, надо вычислить функцию масс, по которой можно судить о минимальной массе невидимого второго компонента и, соответственно, о том, чем он является — планетой, звездой или даже чёрной дырой.
Также по спектроскопическим данным, помимо масс компонентов, можно вычислить расстояние между ними, период обращения и эксцентриситет орбиты. Угол наклона орбиты к лучу зрения выяснить по этим данным невозможно. Поэтому о массе и расстоянии между компонентами можно говорить только как о вычисленных с точностью до угла наклона.
Как и для любого типа объектов, изучаемых астрономами, существуют каталоги спектрально-двойных звёзд. Самый известный и самый обширный из них — «SB9» (от англ. Spectral Binaries). По состоянию на 2013 год в нём 2839 объектов.
Затменно-двойные звёзды
Бывает, что орбитальная плоскость наклонена к лучу зрения под очень маленьким углом: орбиты звёзд такой системы расположены как бы ребром к нам. В такой системе звёзды будут периодически затмевать друг друга, то есть блеск пары будет меняться. Двойные звёзды, у которых наблюдаются такие затмения, называются затменно-двойными или затменно-переменными. Самой известной и первой открытой звездой такого типа является Алголь (Глаз Дьявола) в созвездии Персея.
Микролинзированные двойные
Если на луче зрения между звездой и наблюдателем находится тело с сильным гравитационным полем, то объект будет линзирован. Если бы поле было сильным, то наблюдались бы несколько изображений звезды, но в случае галактических объектов их поле не настолько сильное, чтобы наблюдатель смог различить несколько изображений, и в таком случае говорят о микролинзировании. В случае, если гравирующее тело — двойная звезда, кривая блеска, получаемая при прохождении её вдоль луча зрения, сильно отличается от случая одиночной звезды[6].
С помощью микролинзирования ищутся двойные звезды, где оба компонента — маломассивные коричневые карлики[7].
Явления и феномены, связанные с двойными звёздами
Парадокс Алголя
Этот парадокс сформулирован в середине 20 века советскими астрономами А. Г. Масевич и П. П. Паренаго, обратившими внимание на несоответствие масс компонентов Алголя и их эволюционной стадии. Согласно теории эволюции звёзд, скорость эволюции массивной звезды гораздо больше, чем у звезды с массой, сравнимой с солнечной, или немногим более. Очевидно, что компоненты двойной звезды образовались в одно и то же время, следовательно, массивный компонент должен проэволюционировать раньше, чем маломассивный. Однако в системе Алголя более массивный компонент был моложе.
Объяснение этого парадокса связано с феноменом перетекания масс в тесных двойных системах и впервые предложено американским астрофизиком Д. Кроуфордом. Если предположить, что в ходе эволюции у одного из компонентов появляется возможность переброса массы на соседа, то парадокс снимается[8].
Обмен массами между звёздами
Рассмотрим приближение тесной двойной системы (носящие имя приближения Роша):
- Звезды считаются точечными массами и их собственным моментом осевого вращения можно пренебречь по сравнению с орбитальным
- Компоненты вращаются синхронно.
- Орбита круговая

Тогда для компонентов M1 и M2 с суммой больших полуосей a=a1+a2 введём систему координат, синхронную с орбитальным вращением ТДС. Центр отсчёта находится в центре звезды M1, ось X направлена от M1 к M2, а ось Z — вдоль вектора вращения. Тогда запишем потенциал, связанный с гравитационными полями компонентов и центробежной силой[2]:
[math]\displaystyle{ \Phi = - \frac{GM_1}{r_1}- \frac{GM_2}{r_2}-\frac{1}{2}\omega^2\left[(x-\mu a)^2+y^2\right] }[/math],
где r1= √x2+y2+z2 , r2= √(x-a)2+y2+z2 , μ= M2/(M1+M2), а ω — частота вращения по орбите компонентов. Используя третий закон Кеплера, потенциал Роша можно переписать следующим образом:
[math]\displaystyle{ \Phi = -\frac{1}{2}\omega^2a^2\Omega_R }[/math],
где безразмерный потенциал:
[math]\displaystyle{ \Omega_R = \frac{2}{(1+q)(r_1/a) } +\frac{2}{(1+q)(r_2/a) } +\frac{(x-\mu a)^2+y^2}{a^2} }[/math],
где q = M2/M1
Эквипотенциали находятся из уравнения Φ(x,y,z)=const. Вблизи центров звёзд они мало отличаются от сферических, но по мере удаления отклонения от сферической симметрии становятся сильнее. В итоге обе поверхности смыкаются в точке Лагранжа L1. Это означает, что потенциальный барьер в этой точке равен 0, и частицы с поверхности звезды, находящие вблизи этой точки, способны перейти внутрь полости Роша соседней звезды, вследствие теплового хаотического движения[2].
Новые
Новыми называют звёзды, кратковременно (недели, месяцы) увеличивающие свою светимость в тысячи (до сотен тысяч) раз. По результатам исследований, все такие звёзды являются двойными, одна из компонент является белым карликом, а вторая — звездой обычной плотности, полностью заполняющей свою полость Роша.
Рентгеновские двойные
Рентгеновскими двойными называют тесные пары, где одна из звёзд — компактный объект, нейтронная звезда или чёрная дыра, и жёсткое излучение возникает в результате падения вещества обычной звезды (достигшей границ полости Роша) на аккреционный диск, образующийся вокруг компактного компонента пары.
Симбиотические звёзды
Взаимодействующие двойные системы, состоящие из красного гиганта и белого карлика, окружённых общей туманностью. Для них характерны сложные спектры, где наряду с полосами поглощения (например, TiO) присутствуют эмиссионные линии, характерные для туманностей (ОIII, NeIII и т. п.). Симбиотические звёзды являются переменными с периодами в несколько сотен дней, для них характерны новоподобные вспышки, во время которых их блеск увеличивается на две-три звёздных величины.
Симбиотические звёзды представляют собой относительно кратковременный, но чрезвычайно важный и богатый своими астрофизическими проявлениями этап в эволюции двойных звёздных систем умеренных масс с начальными периодами обращения 1—100 лет.
Барстеры
Разновидность рентгеновских двойных, дающих излучение короткими вспышками (секунды) с промежутками в десятки секунд.
Сверхновые типа Ia
Такие сверхновые образуются в двойной системе, когда при аккреции масса компактного компонента (белый карлик) достигает предела Чандрасекара, либо происходит углеродный взрыв.
Происхождение и эволюция
Механизм формирования одиночной звезды изучен довольно хорошо — это сжатие молекулярного облака из-за гравитационной неустойчивости. Также удалось установить функцию распределения начальных масс. Очевидно, что сценарий формирования двойной звезды должен быть таким же, но с дополнительными модификациями. Также он должен объяснять следующие известные факты[9]:
- Частота двойных. В среднем она составляет 50 %, но различна для звёзд разных спектральных классов. Для О-звёзд это порядка 70 %, для звёзд типа Солнца (спектральный класс G) это близко к 50 %, а для спектрального класса M около 30 %.
- Распределение периода.
- Эксцентриситет у двойных звёзд может принимать любое значение 0<e<1, с медианным значением e=0.55. Можно утверждать, что нет какого-либо предпочтительного значения, и орбиты с высоким эксцентриситетом—обычное явление.
- Соотношение масс. Распределение соотношения масс q= M1/ M2 является самым сложным для измерения, так как влияние эффектов селекции велико, но на данный момент считается, что распределение однородно и лежит в пределах 0.2<q<1. Таким образом, двойные звезды стремятся иметь компоненты одинаковой массы гораздо сильнее, чем предсказывает начальная функция масс.
На данный момент нет окончательного понимания, какие именно надо вносить модификации, и какие факторы и механизмы играют здесь решающую роль. Все предложенные на данный момент теории можно поделить по тому, какой механизм формирования в них используется[10]:
- Теории с промежуточным ядром
- Теории с промежуточным диском
- Динамические теории
Теории с промежуточным ядром
Самый многочисленный класс теорий. В них формирование идёт за счёт быстрого или раннего разделения протооблака.
Самая ранняя из них считает, что в ходе коллапсирования из-за различного рода нестабильностей облако распадается на локальные джинсовские массы, растущие до тех пор, пока наименьшая из них перестанет быть оптически прозрачной и более не может эффективно охлаждаться. Но при этом расчётная функция масс звёзд не совпадает с наблюдаемой.
Ещё одна из ранних теорий предполагала размножение коллапсирующих ядер, вследствие деформации в различные эллиптические фигуры.
Современные же теории рассматриваемого типа считают, что основная причина фрагментации — рост внутренней энергии и энергии вращения по мере сжатия облака[10].
Теории с промежуточным диском
В теориях с динамическим диском образование происходит в ходе фрагментации протозвёздного диска, то есть гораздо позднее, чем в теориях с промежуточным ядром. Для этого необходим довольно массивный диск, восприимчивый к гравитационным нестабильностям, и газ которого эффективно охлаждается. Тогда могут возникнуть несколько компаньонов, лежащих в одной плоскости, которые аккрецируют газ из родительского диска.
В последнее время количество компьютерных расчётов подобных теорий сильно увеличилось. В рамках подобного подхода хорошо объясняется происхождение тесных двойных систем, а также иерархических систем различной кратности.
Динамические теории
Последний механизм предполагает, что двойные звезды образовались в ходе динамических процессов, спровоцированных соревновательной аккрецией. В данном сценарии предполагается, что молекулярное облако из-за различного рода турбуленций внутри него формирует сгустки приблизительно джинсовской массы. Эти сгустки, взаимодействуя между собой, соревнуются за вещество исходного облака. В таких условиях хорошо работает как уже упомянутая модель с промежуточным диском, так и иные механизмы, речь о которых пойдёт ниже. Вдобавок динамическое трение протозвёзд с окружающим газом сближает компоненты.
В качестве одного из механизмов, работающего в данных условиях, предлагается комбинация фрагментации с промежуточным ядром и динамической гипотезы. Это позволяет воспроизвести частоту кратных звёзд в звёздных скоплениях. Однако на данный момент механизм фрагментации точно не описан.
Другой механизм предполагает рост сечения гравитационного взаимодействия у диска до тех пор, пока не будет захвачена близлежащая звезда. Хотя такой механизм вполне подходит для массивных звёзд, но совершенно не годится для маломассивных и вряд ли является доминирующим при образовании двойных звёзд[10].
Экзопланеты в двойных системах

Из более чем 800 ныне известных экзопланет число обращающихся вокруг одиночных звёзд значительно превышает число планет, найденных в звёздных системах разной кратности. По последним данным последних насчитывается 64[11].
Экзопланеты в двойных системах принято разделять по конфигурациям их орбит[11]:
- Экзопланеты S-класса обращаются вокруг одного из компонентов (например OGLE-2013-BLG-0341LB b). Таковых 57.
- К P-классу относят планеты, обращающиеся вокруг обоих компонентов. Таковые обнаружены у NN Ser, DP Leo, HU Aqr, UZ For, Kepler-16 (AB)b, Kepler-34 (AB)b и Kepler-35 (AB)b.
Если попытаться провести статистику, то выяснится[11]:
- Значительная часть планет обитают в системах, где компоненты разделены в пределах от 35 до 100 а. е., концентрируясь вокруг значения в 20 а. е.
- Планеты в широких системах (> 100 а. е.) имеют массу от 0,01 до 10 MJ (почти как и для одиночных звёзд), в то время как массы планет для систем с меньшим разделением лежат от 0,1 до 10 MJ
- Планеты в широких системах всегда одиночные
- Распределение эксцентриситетов орбиты отличается от одиночных, достигая значений e = 0,925 и e = 0,935.
Важные особенности процессов формирования
Обрезание протопланетного диска. В то время как у одиночных звёзд протопланетный диск может тянуться вплоть до пояса Койпера (30-50 а. е.), то в двойных звёзд его размер обрезается воздействием второго компонента. Таким образом протяжённость протопланетного диска в 2-5 раз меньше расстояния между компонентами.
Искривление протопланетного диска. Оставшийся после обрезания диск продолжает испытывать влияние второго компонента и начинает вытягиваться, деформироваться, сплетаться и даже разрываться. Также такой диск начинает прецессировать.
Сокращения время жизни протопланетного диска. Для широких двойных, как и для одиночных время жизни протопланетного диска составляет 1-10 млн лет, однако для систем с разделением < 40 а. е. время жизни диска должно находиться в пределах 0,1-1 млн лет.
Планетезимальный сценарий образования
Этот раздел статьи ещё не написан. |
Несовместные сценарии образования
Существуют сценарии, в которых изначальная, сразу после формирования, конфигурация планетной системы отличается от текущей и была достигнута в ходе дальнейшей эволюции.
- Один из таких сценариев — захват планеты у другой звезды. Так как двойная звезда имеет гораздо больше сечения взаимодействия, то и вероятность столкновения и захват планеты у другой звезды существенно выше.
- Второй сценарий предполагает, что в ходе эволюции одного из компонентов, уже на стадиях после главной последовательности в изначальной планетарной системе возникают нестабильности. В результате которых планета покидает изначальную орбиту и становится общей для обоих компонент.
Астрономические данные и их анализ
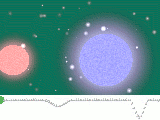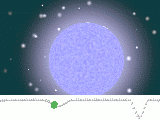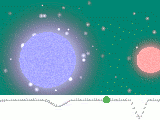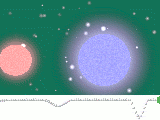
Кривые блеска
|
|

|
|
| Примеры кривых блеска для разделённой и тесной двойной системы |
В случае, когда двойная звезда является затменной, то становится возможным построить зависимость интегрального блеска от времени. Переменность блеска на этой кривой будет зависеть от [12]:
- Самих затмений
- Эффектов элипсоидальности.
- Эффектов отражения, а вернее переработки излучения одной звезды в атмосфере другой.
Однако анализ только самих затмений, когда компоненты сферически симметричны и отсутствуют эффекты отражения, сводится к решению следующей системы уравнений[12]:
[math]\displaystyle{ 1-l_1(\Delta) =\iint\limits_{S(\Delta)}I_a(\xi)I_c(\rho) d\sigma }[/math]
[math]\displaystyle{ 1-l_2(\Delta) =\iint\limits_{S(\Delta)}I_c(\xi)I_a(\rho) d\sigma }[/math]
[math]\displaystyle{ \int\limits_0^{r_{\xi c}} I_c(\xi)2\pi\xi d\xi + \int\limits_0^{r_{\rho c}}I_c(\rho)2\pi\rho d\rho =1 }[/math]
где ξ, ρ — полярные расстояния на диске первой и второй звезды, Ia — функция поглощения излучения одной звезды атмосферой другой, Ic — функция яркости площадок dσ у различных компонентов, Δ — область перекрытия, rξc,rρc — полные радиусы первой и второй звезды.
Решение этой системы без априорных предположений невозможно. Ровно как и анализ более сложных случаев с элипсоидальной формой компонентов и эффектами отражения, существенных в различных вариантах тесных двойных систем. Поэтому все современные способы анализа кривых блеска тем или иным образом вводят модельные предположения, параметры которых находят путём другого рода наблюдений[12].
Кривые лучевых скоростей
Если двойная звезда наблюдается спектроскопически, то есть является спектроскопической двойной звездой, то можно построить зависимость изменения лучевых скоростей компонентов от времени. Если предположить, что орбита круговая, то можно записать следующее[2]:
[math]\displaystyle{ V_s = V_0sin(i) = \frac{2\pi}{P}a\sin(i) }[/math],
где Vs — лучевая скорость компонента, i — наклонение орбиты к лучу зрения, P — период, a — радиус орбиты компонента. Теперь, если в эту формулу подставить третий закон Кеплера, имеем:
[math]\displaystyle{ V_s =\frac{2\pi}{P}\frac{M_s}{M_s+M_2}\sin(i) }[/math],
где Ms — масса исследуемого компонента, M2 — масса второго компонента. Таким образом, наблюдая оба компонента можно определить соотношение масс звёзд, составляющих двойную. Если повторно использовать третий закон Кеплера, то последние приводится к следующему:
[math]\displaystyle{ f(M_2)=\frac{PV_{s1}}{2\pi G} }[/math],
где G — гравитационная постоянная, а f(M2) — функция масс звезды и по определению равна:
[math]\displaystyle{ f(M_2)\equiv \frac{ (M_2\sin(i))^3 }{(M_1+M_2)^2} }[/math].
В случае, если орбита не круговая, а имеет эксцентриситет, то можно показать, что для функции масса орбитальный период P должен быть домножен на фактор [math]\displaystyle{ (1-e^2)^{3/2} }[/math].
Если второй компонент не наблюдается, то функция f(M2) служит нижним пределом его массы.
Стоит отметить, что изучая только кривые лучевых скоростей невозможно определить все параметры двойной системы, всегда будет присутствовать неопределённость в виде неизвестного угла наклонения орбиты[2].
Определение масс компонентов
Практически всегда гравитационное взаимодействие между двумя звёздами описывается с достаточной точностью законами Ньютона и законами Кеплера, являющимися следствием законов Ньютона. Но для описания двойных пульсаров (см. пульсар Тейлора — Халса) приходится привлекать ОТО. Изучая наблюдательные проявления релятивистских эффектов, можно ещё раз проверить точность теории относительности.
Третий закон Кеплера связывает период обращения с расстоянием между компонентами и массой системы:
- [math]\displaystyle{ P=2\pi\sqrt\frac{a^3}{G(M_1+M_2)} }[/math],
где [math]\displaystyle{ P }[/math] — период обращения, [math]\displaystyle{ a }[/math] — большая полуось системы, [math]\displaystyle{ M_1 }[/math] и [math]\displaystyle{ M_2 }[/math] — массы компонентов, [math]\displaystyle{ G }[/math] — гравитационная постоянная. Для визуально-двойной системы есть возможность определить орбиты обоих компонентов, рассчитать период и полуось, а также отношение масс. Но часто о двойственности системы можно судить только по спектральным данным (спектрально-двойные). По движению спектральных линий можно определить лучевые скорости одного компонента, а в редких случаях и сразу двух компонентов. Если известна лучевая скорость только одного компонента, то полную информацию о массах получить нельзя, но можно построить функцию масс и определить верхнюю границу массы второго компонента, а значит сказать, может ли он являться чёрной дырой или нейтронной звездой.
История открытия и изучения
Первым выдвинул идею о существовании двойных звёзд Джон Мичелл (Reverend John Michell). На выступлении в Королевском обществе в 1767 году он предположил, что многие звезды, видимые как двойные, действительно могут быть физически связаны. Наблюдательные подтверждения этой гипотезы были опубликованы сэром Уильямом Гершелем в 1802[13].
См. также
- Кратная звезда
- Тесная двойная система
- Оптически-двойная звезда
- PSR J0737-3039
- PSR B1913+16
- 2MASS J18082002-5104378
Примечания
- ↑ 1,0 1,1 А.А. Киселев. Двойные звезды. Астронет (12 декабря 2005). Дата обращения: 27 апреля 2013. Архивировано 5 апреля 2013 года.
- ↑ 2,0 2,1 2,2 2,3 2,4 А. В. Засов, К. А. Постнов. Общая астрофизика. — Фрязино: ВЕК 2, 2006. — С. 208—223. — 398 с. — 1500 экз. — ISBN 5-85099-169-7.
- ↑ Speckle Interferometry and Orbits of «Fast» Visual Binaries
- ↑ V. V. Makarov and G. H. Kaplan. Statistical Constraints for Astrometric Binaries with Nonlinear Motion. — .
- ↑ Pope, Benjamin; Martinache, Frantz; Tuthill, Peter. Dancing in the Dark: New Brown Dwarf Binaries from Kernel Phase Interferometry. — 2013. — .
- ↑ Gravitational Microlensing of Binary Stars: Light Curve Synthesis. — 1997. (недоступная ссылка)
- ↑ Choi, J.-Y.; Han, C.; Udalski, A.; Sumi, T etc. Microlensing Discovery of a Population of Very Tight, Very Low Mass Binary Brown Dwarfs. — 2013. — .
- ↑ В.М. Липунов. Парадокс Алголя. Дата обращения: 11 мая 2013. Архивировано 4 марта 2016 года.
- ↑ Richard B.Larson. Implications of binary properties for theories of star formation (англ.). — 2001. Архивировано 28 мая 2008 года.
- ↑ 10,0 10,1 10,2 Kaitlin M. Kratter. The Formation of Binaries (англ.). — 2011. — . — arXiv:1109.3740.
- ↑ 11,0 11,1 11,2 Zhou, Ji-Lin; Xie, Ji-Wei; Liu, Hui-Gen; Zhang, Hui; Sun, Yi-Sui. Forming different planetary systems.
- ↑ 12,0 12,1 12,2 А. В. Гончарский, А.М. Черепащук, А.Г. Ягола. Некорректные задачи астрофизики. — Москва: Наука, 1985. — С. 68—101. — 351 с. — 2500 экз.
- ↑ Hans Zinnecker. Binary Stars: Historical Millestones (англ.) : материалы конференции. — The formation binary stars IAU symposium, 2001. — Vol. 200. Архивировано 28 мая 2008 года.
Литература
- Двойные звёзды / Куликовский П. Г. // Физика космоса: Маленькая энциклопедия / Редкол.: Р. А. Сюняев (Гл. ред.) и др. — 2-е изд. — М. : Советская энциклопедия, 1986. — С. 238—241. — 783 с. — 70 000 экз.
- Липунов В. М. В мире двойных звёзд. — М.: Наука. Главная редакция физико-математической литературы, 1986. — 208 с. — (Библиотечка «Квант»; Выл. 52). — 111 000 экз.
Ссылки
- BinSim — Binary Star Visualisations Software (англ.)
- Спектрально-двойные звёзды
- Orbit of an astrometric binary (недоступная ссылка)