Геоид

1. Мировой океан
2. Земной эллипсоид
3. Отвесные линии
4. Суша.
5. Геоид
Гео́ид (от др.-греч. γῆ — Земля и др.-греч. εἶδος — вид, букв. — «нечто подобное Земле») — эквипотенциальная поверхность земного поля тяжести (уровенная поверхность), приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками. Отличие реального среднего уровня моря от геоида может достигать 1 м из-за различия температуры и солености, атмосферного давления и т. п.[1] По определению эквипотенциальной поверхности, поверхность геоида везде перпендикулярна отвесной линии. Иными словами, геоид — это форма, которую поверхность океана могла бы принять под действием силы тяжести и вращения Земли, если бы отсутствовали другие воздействия, такие как ветры и приливы. Точная конфигурация геоида может быть установлена только путём расчётов, основанных на измерениях гравитационного поля Земли. Такие расчёты с высокой точностью были проведены только после возникновения космической геодезии в конце XX века.
Некоторые авторы обозначают вышеописанную поверхность не как «геоид», а термином «основная уровенная поверхность», в то время как сам «геоид» определяется как 3-мерное тело, ограниченное этой поверхностью[2].
История
Впервые фигуру геоида описал немецкий математик К. Ф. Гаусс, который определял её как «математическую фигуру Земли» — гладкую, но неправильную поверхность (англ. irregular surface), форма которой обусловлена неравномерным распределением масс внутри и на поверхности Земли.
Термин «геоид» был введён в геодезию 1873 году учеником Гаусса, немецким математиком и физиком Иоганном Бенедиктом Листингом[3] для обозначения геометрической фигуры, более точно, чем эллипсоид вращения, отражающей уникальную форму планеты Земля.
Определение термина «геоид» в последующем неоднократно уточнялось. В настоящее время в РФ определение термина «геоид» регламентировано ГОСТ 22268-76, в котором оно сформулировано следующим образом: «фигура Земли, образованная уровенной поверхностью, совпадающей с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженной под материками»[4].
Описание и применение
Геоид является поверхностью, относительно которой ведётся отсчёт высот над уровнем моря, в силу чего точное знание параметров геоида необходимо, в частности, в навигации — для определения высоты над уровнем моря на основе геодезической (эллипсоидальной) высоты, измеряемой GPS-приёмниками, а также в физической океанологии — для определения высот морской поверхности.
Поверхность геоида является неправильной[англ.], в отличие от эталонного эллипсоида (который является математическим идеализированным представлением формы Земли), но значительно более гладкая, чем реальная физическая поверхность Земли. Хотя реальная земная поверхность имеет отклонения высот от уровня моря от +8,848 м (гора Эверест) до −11,034 м (Марианская впадина), отклонение геоида от эллипсоида колеблется от +85 м (Исландия) до −106 м (южная Индия), в общей сложности менее 200 м[5].
Если бы Мировой океан имел постоянную плотность, не подвергался воздействию приливов, течений и других погодных условий, его поверхность была бы близка к геоиду. Постоянное отклонение между геоидом и уровнем моря называется высотой морской поверхности. Если бы толщи континентов были пересечены рядом туннелей или каналов, уровень моря в этих каналах также почти совпадал бы с геоидом. В действительности, геоид не имеет реального физического носителя под континентами, но геодезисты могут вывести высоты точек континента над этой воображаемой поверхностью, путём нивелирования.
Будучи эквипотенциальной поверхностью, геоид, по определению, является поверхностью, к каждой точке которой сила тяжести направлена перпендикулярно. Это означает, что при путешествии на корабле человек не замечает волнистости геоида; отвес (вертикальная линия) всегда перпендикулярен геоиду. Аналогично, уровень моря всегда будет параллелен геоиду.
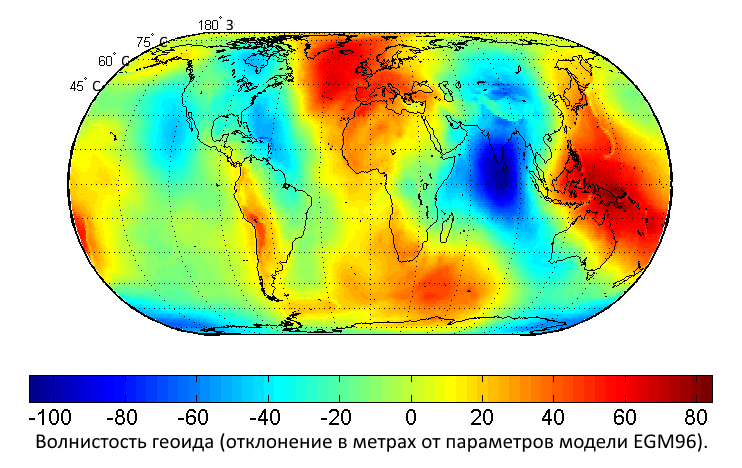
Волнистость геоида
Волнистость геоида — характеристика, показывающая разность высот геоида и референц-эллипсоида. Волнистость не стандартизирована, так как разные страны используют в качестве эталона разные величины уровня моря — например, в России исходными считаются Кронштадтский футшток и Балтийская система высот. а в США текущий датум — NAVD88. Часто волнистость описывают применительно к геоиду модели EGM96[англ.][6].
Связь с системой GPS
На картах и в обычной практике высота над уровнем моря (например, ортометрическая высота) используется для указания высоты возвышенностей, в то время как высота в модели референц-эллипсоида определяется с помощью спутниковой навигационной системы GPS.
Разность [math]\displaystyle{ N }[/math] между геодезической (эллипсоидальной) высотой [math]\displaystyle{ h }[/math] и ортометрической высотой [math]\displaystyle{ H }[/math] можно рассчитать с помощью формулы
- [math]\displaystyle{ N=h-H }[/math].
Аналогично, разность [math]\displaystyle{ \zeta }[/math] между эллипсоидальной высотой [math]\displaystyle{ h }[/math] и нормальной высотой [math]\displaystyle{ H_N }[/math] можно рассчитать с помощью формулы
- [math]\displaystyle{ \zeta=h-H_N }[/math].
Современные GPS-приёмники имеют устройства геолокации, привязывающие их текущее местоположение к координатам эллипсоида WGS. Это позволяет перевести значение высоты над эллипсоидом WGS, например, в значение высоты над геоидом модели EGM96.
Аппроксимация с помощью сферических функций

Для аппроксимации формы геоида часто используются сферические функции. В настоящее время наилучшей подобной аппроксимацией является модель EGM96 (Earth Gravity Model 1996)[7], разработанная в международном научном проекте под руководством Национального агентства геопространственной разведки (NGA) США. Математическое описание невращающейся части потенциальной функции в этой модели[8]:
- [math]\displaystyle{ V=\frac{GM}{r}\left(1+{\sum_{n=2}^{n_\text{max}}}\left(\frac{a}{r}\right)^n{\sum_{m=0}^n} \overline{P}_{nm}(\sin\phi)\left[\overline{C}_{nm}\cos m\lambda+\overline{S}_{nm}\sin m\lambda\right]\right), }[/math]
где [math]\displaystyle{ \phi\ }[/math] и [math]\displaystyle{ \lambda\ }[/math] являются геоцентрическими (сферическими) широтой и долготой соответственно, [math]\displaystyle{ \overline{P}_{nm} }[/math] являются полностью нормализованными ассоциированными полиномами Лежандра[англ.] степени [math]\displaystyle{ n\ }[/math] и порядка [math]\displaystyle{ m\ }[/math], и [math]\displaystyle{ \overline{C}_{nm} }[/math] и [math]\displaystyle{ \overline{S}_{nm} }[/math] являются числовыми коэффициентами модели, основанными на измеренных данных. Приведённое выше уравнение описывает гравитационный потенциал Земли [math]\displaystyle{ V\ }[/math], а не сам геоид в месте с координатами [math]\displaystyle{ \phi,\;\lambda,\;r\ }[/math]; координата [math]\displaystyle{ r\ }[/math] — геоцентрический радиус, то есть расстояние от центра Земли. Градиент этого потенциала также даёт модель ускорения силы тяжести. Модель EGM96 содержит полный набор коэффициентов для степеней порядка 360 (то есть [math]\displaystyle{ n_\text{max} = 360 }[/math]), описывающих в геоиде детали размером до 55 км (или 110 км, в зависимости от выбранного разрешения). Количество коэффициентов [math]\displaystyle{ \overline{C}_{nm} }[/math] and [math]\displaystyle{ \overline{S}_{nm} }[/math] можно определить, сначала наблюдая в уравнении для V, что для конкретного значения n существует два коэффициента для каждого значения m, кроме m = 0. Существует единственный коэффициент при m = 0, так как [math]\displaystyle{ \sin (0\lambda) = 0 }[/math]. Таким образом, существует (2n + 1) коэффициентов для каждого значения n. Исходя из этого, по формуле [math]\displaystyle{ \sum_{I=1}^{L}I = L(L+1)/2 }[/math] получаем, что общее число коэффициентов определяется при значении в модели EGM96 [math]\displaystyle{ n_\text{max} = 360 }[/math],
- [math]\displaystyle{ \sum_{n=2}^{n_\text{max}}(2n+1) = n_\text{max}(n_\text{max}+1) + n_\text{max} - 3 = 130317 }[/math].
Во многих случаях использование полного набора коэффициентов представляется неоправданно сложным, поэтому геоид рассчитывается с использованием лишь нескольких десятков коэффициентов.
В настоящее время в стадии разработки находятся модели с ещё более высоким разрешением. Например, многие из разработчиков модели EGM96 работают над обновленной моделью, которая должна включать спутниковые измерения гравитационного потенциала (в частности, в рамах проекта GRACE) и поддерживать значение [math]\displaystyle{ n_\text{max} = 2160 }[/math] (что означает более 4 миллионов коэффициентов)[9].
NGA объявило о размещении для публичного доступа модели EGM2008, завершённой до степени n=2159, и содержащей дополнительные коэффициенты, распространяющиеся до степени 2190 и m=2159[10].
Квазигеоид
Фигура геоида зависит от распределения масс и плотностей в теле Земли[источник не указан 1885 дней]. Поскольку она не имеет точного математического выражения и является практически неопределяемой модельно, в геодезических измерениях в России и некоторых других странах вместо геоида используется одна из его аппроксимаций — квазигеоид. Квазигеоид, в отличие от геоида, однозначно определяется по результатам измерений, совпадает с геоидом на территории Мирового океана и очень близок к геоиду на суше, отклоняясь лишь на несколько сантиметров на равнинной местности и не более чем на 2 метра в высоких горах.
Аномалии
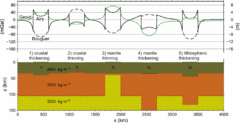
Гравитационные аномалии, вызванные аномальным распределением плотности земного шара, приводят к изменениям высоты поверхности геоида[11]. Таким образом, измерения геоида помогают понять внутреннюю структуру нашей планеты. Расчёты показывают, что геоидальная сигнатура утолщённой земной коры (например, в тектогенезе, вызванном столкновением материков) является положительной, в противоположность тому, что следует ожидать, если утолщение затрагивает всю литосферу.

Временные флуктуации
Ряд исследовательских проектов с использованием спутников, такие как GOCE и GRACE, позволили изучить временны́е флуктуации сигналов геоида. Первые продукты, основанные на спутниковых данных проекта GOCE, стали доступны онлайн в июне 2010 года с использованием сервисов для пользователей ЕКА[12][13]. ЕКА запустило спутник в марте 2009 года с целью создать карту гравитационного потенциала Земли с не имевшей аналогов точностью и пространственным разрешением. 31 марта 2011 года новая модель геоида была представлена на Четвёртом международном семинаре для пользователей GOCE в Мюнхенском техническом университете[14]. Исследования с использованием изменяющегося во времени геоида, рассчитанные по данным GRACE, позволили получить информацию о глобальных гидрологических циклах[15], балансах массы ледниковых щитов[16] и гляциоизостазии[17]. Данные экспериментов GRACE также могут использоваться для определения вязкости мантии Земли[18].
Другие небесные тела
Понятие геоида было распространено на другие планеты Солнечной системы, их спутники, а также астероиды[19]. Так, аналогичная эквипотенциальная поверхность Луны называется селеноидом[20][21].
Геоид Марса был измерен с использованием автоматических межпланетных станций, в частности, Маринер-9 и «Викинг». Основные отклонения от идеального эллипсоида находятся в районе вулканического плато Тарсис, известного огромными размерами, и его антиподов[22].
См. также
Примечания
- ↑ Теория фигуры Земли. Дата обращения: 11 октября 2019. Архивировано 16 декабря 2019 года.
- ↑ [www.mining-enc.ru/g/geoid/ Горная энциклопедия: определение геоида.]
- ↑ Боголюбов, 1983, с. 288.
- ↑ ГОСТ 22268-76 Геодезия. Термины и определения (с Изменением N 1). Дата обращения: 12 октября 2019. Архивировано 3 декабря 2019 года.
- ↑ Earth's Gravity Definition. GRACE - Gravity Recovery and Climate Experiment. Center for Space Research (University of Texas at Austin) / Texas Space Grant Consortium (11 февраля 2004). Дата обращения: 22 января 2018. Архивировано 6 февраля 2019 года.
- ↑ WGS 84, N=M=180 Earth Gravitational Model. NGA: Office of Geomatics. National Geospatial-Intelligence Agency. Дата обращения: 17 декабря 2016. Архивировано 18 декабря 2016 года.
- ↑ DoD World Geodetic System 1984. NGA: Office of Geomatics. National Geospatial-Intelligence Agency. Дата обращения: 16 декабря 2016. Архивировано 26 января 2021 года.
- ↑ Smith, Dru A. There is no such thing as "The" EGM96 geoid: Subtle points on the use of a global geopotential model // IGeS Bulletin No. 8. — Milan, Italy: International Geoid Service, 1998. — С. 17—28.
- ↑ Pavlis, N.K., S.A. Holmes. S. Kenyon, D. Schmit, R. Trimmer, «Gravitational potential expansion to degree 2160», IAG International Symposium, gravity, geoid and Space Mission GGSM2004, Porto, Portugal, 2004.
- ↑ Earth Gravitational Model 2008 (EGM2008). nga.mil. Дата обращения: 6 июля 2020. Архивировано 6 августа 2020 года.
- ↑ Квазигеоид Молоденского. Дата обращения: 25 ноября 2019. Архивировано 18 июля 2019 года.
- ↑ ESA makes first GOCE dataset available. GOCE. European Space Agency (9 июня 2010). Дата обращения: 22 декабря 2016. Архивировано 20 октября 2012 года.
- ↑ GOCE giving new insights into Earth's gravity. GOCE. European Space Agency (29 июня 2010). Дата обращения: 22 декабря 2016. Архивировано 2 июля 2010 года.
- ↑ Earth's gravity revealed in unprecedented detail. GOCE. European Space Agency (31 марта 2011). Дата обращения: 22 декабря 2016. Архивировано 26 ноября 2012 года.
- ↑ Schmidt, R; Schwintzer, P; Flechtner, F; Reigber, C; Guntner, A; Doll, P; Ramillien, G; Cazenave, A; Petrovic, S. GRACE observations of changes in continental water storage (англ.) // Global and Planetary Change[англ.] : journal. — 2006. — Vol. 50, no. 1—2. — P. 112—126. — doi:10.1016/j.gloplacha.2004.11.018. — .
- ↑ Ramillien, G; Lombard, A; Cazenave, A; Ivins, E; Llubes, M; Remy, F; Biancale, R. Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE (англ.) // Global and Planetary Change[англ.] : journal. — 2006. — Vol. 53, no. 3. — P. 198. — doi:10.1016/j.gloplacha.2006.06.003. — .
- ↑ Vanderwal, W; Wu, P; Sideris, M; Shum, C. Use of GRACE determined secular gravity rates for glacial isostatic adjustment studies in North-America (англ.) // Journal of Geodynamics : journal. — 2008. — Vol. 46, no. 3—5. — P. 144. — doi:10.1016/j.jog.2008.03.007. — .
- ↑ Paulson, Archie; Zhong, Shijie; Wahr, John. Inference of mantle viscosity from GRACE and relative sea level data (англ.) // Geophysical Journal International[англ.] : journal. — 2007. — Vol. 171, no. 2. — P. 497. — doi:10.1111/j.1365-246X.2007.03556.x. — .
- ↑ Wieczorek, M. A. Gravity and Topography of the Terrestrial Planets // Treatise on Geophysics. — 2007. — С. 165—206. — ISBN 9780444527486. — doi:10.1016/B978-044452748-6.00156-5.
- ↑ К. А. Куликов, В. Б. Гуревич, Основы лунной астрометрии, 1972
- ↑ Л. П. Крысин, Толковый словарь иностранных слов, 1998
- ↑ Cattermole, Peter. Mars The story of the Red Planet. — Dordrecht: Springer Netherlands, 1992. — С. 185. — ISBN 9789401123068.
Литература
- Боголюбов А. Н. Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
- Парийский Н. Н. О некоторых следствиях несферичности Земли // Медленные деформации Земли и её вращение. — М., 1985. — С. 35—39.
- H. Moritz. A contemporary perspective of geoid structure // Journal of Geodetic Science. — Versita, 2011. — Т. 1, № March. — С. 82—87. — doi:10.2478/v10156-010-0010-7. — .
- CHAPTER V PHYSICAL GEODESY. www.ngs.noaa.gov. NOAA. Дата обращения: 15 июня 2016.
Ссылки
- В. Л. Пантелеев. «Теория фигуры Земли» (курс лекций)
- [1] 3D-визуализация геоида
- Main NGA (was NIMA) page on Earth gravity models
- International Geoid Service (IGeS) Архивная копия от 5 апреля 2014 на Wayback Machine
- EGM96 NASA GSFC Earth gravity model
- Earth Gravitational Model 2008 (EGM2008, Released in July 2008)
- NOAA Geoid webpage
- International Centre for Global Earth Models (ICGEM)
- GeographicLib provides a utility GeoidEval (with source code) to evaluate the geoid height for the EGM84, EGM96, and EGM2008 earth gravity models. Here is an online version of GeoidEval.
- Kiamehr’s Geoid Home Page
- A free windows calculator which yields, among other calculation, the height difference between EGM96 geoid and mean sea level at every point on earth
- Geoid tutorial from Li and Gotze (964KB pdf file)
- Geoid tutorial at GRACE website
- Precise Geoid Determination Based on the Least-Squares Modification of Stokes’ Formula(PhD Thesis PDF)
- View EGM2008, EGM96 and EGM84 on Google Maps
- Geoid Height Calculator | Software | UNAVCO. www.unavco.org. Unavco. Дата обращения: 15 июня 2016.