Префиксная сумма

В информатике префиксная сумма, кумулятивная сумма, инклюзивное сканирование или просто сканирование последовательности чисел x0, x1, x2, … называется последовательность чисел y0, y1, y2, …, являющаяся префиксной суммой от входной последовательности:

y₀ = x₀

y₁ = x₀ + x₁

y₂ = x₀ + x₁+ x₂

…

Например, префиксными суммами натуральных чисел являются треугольные числа:

входные числа	1	2	3	4	5	6	…
префиксная сумма	1	3	6	10	15	21	…

Префиксные суммы тривиальны для вычисления в последовательных моделях вычислений, путем применения формулы y_i = y_{i − 1} + x_i для вычисления каждого выходного значения в порядке последовательности. Тем не менее, несмотря на простоту вычислений, префиксные суммы являются полезным примитивом в некоторых алгоритмах, таких как сортировка подсчетом,^[1]^[2] и они составляют основу функции сканирования более высокого порядка в функциональных языках программирования. Суммы префиксов также широко изучались в параллельных алгоритмах, и как тестовая задача, которую нужно решить, и как полезный примитив для использования в качестве подпрограммы в других параллельных алгоритмах.^[3]^[4]^[5]

Теоретически, префиксная сумма требует только двоичного ассоциативного оператора ⊕, что делает ее полезной во многих алгоритмах: от вычисления хорошо разделенных парных декомпозиций точек до обработки строк.^[6]^[7]

Математически, операция взятия префиксных сумм может быть обобщена от конечных до бесконечных последовательностей; в этом смысле префиксная сумма известна как частичная сумма ряда. Префиксное суммирование или частичное суммирование образует линейное отображение на векторные пространства конечных или бесконечных последовательностей; их обратные операторы являются конечными разностями.

Сканирование функции высшего порядка

В терминах функционального программирования префиксная сумма может быть обобщена на любую двоичную операцию (не только операцию сложения); функция более высокого порядка, полученная в результате этого обобщения, называется сканированием, и она тесно связана с операцией свертки. Обе операции сканирования и сверки применяют данную двоичную операцию к одной и той же последовательности значений, но отличаются тем, что сканирование возвращает всю последовательность результатов двоичной операции, тогда как свертка возвращает только конечный результат. Например, последовательность факториальных чисел может быть сгенерирована путем сканирования натуральных чисел с использованием умножения вместо сложения:

входные числа	1	2	3	4	5	6	…
префиксные значения	1	2	6	24	120	720	…

Инклюзивные и эксклюзивные сканирования

Языковые и библиотечные реализации сканирования могут быть инклюзивными или эксклюзивными. Инклюзивное сканирование включает в себя ввод x_i при вычислении вывода y_i ([math]\displaystyle{ y_i = \bigoplus_{j=0}^i x_j }[/math]), в то время как эксклюзивное сканирование его не включает ([math]\displaystyle{ y_i = \bigoplus_{j=0}^{i-1} x_j }[/math]). В последнем случае реализации либо оставляют y₀ неопределенным, либо принимают особое значение «x_-1», с помощью которого можно начать сканирование. Эксклюзивные сканы являются более общими в том смысле, что инклюзивное сканирование всегда может быть реализовано в терминах эксклюзивного сканирования (путем последующего комбинирования x_i с y_i), но эксклюзивное сканирование не всегда может быть реализовано в терминах инклюзивного сканирования, как в случае максимума префиксной суммы.

В следующей таблице приведены примеры функций инклюзивного и эксклюзивного сканирования, предоставляемых несколькими языками программирования и библиотеками:

Языки/библиотеки	Инклюзивное сканирование	Эксклюзивное сканирование
Haskell	`scanl1`	`scanl`
MPI	`MPI_Scan`	`MPI_Exscan`
C++	`std::inclusive_scan`	`std::exclusive_scan`
Scala	`scan`
Rust	`scan` Архивная копия от 6 июня 2021 на Wayback Machine

Параллельные алгоритмы

Существуют два ключевых алгоритма для параллельного вычисления префиксной суммы. Первый метод подразумевает меньшую глубину и большую предрасположенность к распараллеливанию, но такой способ недостаточно эффективен. Второй вариант более эффективен, но требует двойную глубину и предлагает меньше вариантов для распараллеливания. Ниже представлены оба алгоритма.

Алгоритм 1: меньшая глубина, большая предрасположенность к распараллеливанию

Hillis and Steele представляют следующий алгоритм параллельной суммы префиксов:^[8]

for [math]\displaystyle{ i \gets 0 }[/math] to [math]\displaystyle{ \lceil\log_2 n\rceil - 1 }[/math] do

for [math]\displaystyle{ j \gets 0 }[/math] to [math]\displaystyle{ n - 1 }[/math] do in parallel

if [math]\displaystyle{ j \lt 2^i }[/math] then

[math]\displaystyle{ x^{i+1}_j \gets x^i_j }[/math]

else

[math]\displaystyle{ x^{i+1}_j \gets x^i_j + x^i_{j - 2^i} }[/math]

Обозначение [math]\displaystyle{ x^i_j }[/math] означает значение j-го элемента массива x на шаге i.

Если учитывать n процессоров для выполнения каждой итерации внутреннего цикла за постоянное время, то алгоритм выполняется за O(log n) времени.

Алгоритм 2: эффективный

Эффективный параллельный алгоритм вычисления префиксной суммы может быть реализован следующим способом:^[3]^[9]^[10]

Вычислить суммы последовательных пар элементов, в которых первый элемент пары имеет четный индекс: z₀ = x₀ + x₁, z₁ = x₂ + x₃ и т. д.
Рекурсивно вычислить префиксную сумму w₀, w₁, w₂, ..., последовательности z₀, z₁, z₂, ...
Выразить каждый член последовательности y₀, y₁, y₂, ... как сумму до двух членов этих промежуточных последовательностей: y₀ = x₀, y₁ = z₀, y₂ = z₀ + x₂, y₃ = w₀, и т. д. Каждое значение y_i, кроме первого, вычисляется либо копированием с позиции вдвое меньшей, чем в последовательности w, либо добавлением значения последовательности x к предыдущему значению y-1_i.

Если входная последовательность имеет размер n, то рекурсия продолжается до глубины O(log n), которая также ограничена временем параллельного выполнения этого алгоритма. Количество операций алгоритма равно O(n), и их можно реализовать на абстрактной параллельной ЭВМ с общей памятью (PRAM) с количеством процессоров O(n/log n) без какого-либо асимптотического замедления путем назначения нескольких индексов каждому процессору в вариантах алгоритма, для которых больше элементов, чем процессоров.^[3]

Сравнение алгоритмов

Каждый из предыдущих алгоритмов выполняется за O(log n). Тем не менее, первый делает ровно log₂ n шагов, а второй требует 2 log₂ n − 2 шага. Для приведенных примеров с 16 входами Алгоритм 1 является 12-параллельным (49 единиц работы, разделенных на 4), а Алгоритм 2 — только 4-параллельным (26 единиц работы, разделенных на 6). Однако Алгоритм 2 эффективен с точки зрения работы он выполняет только постоянный коэффициент (2) объема работы, требуемого последовательным алгоритмом, а Алгоритм 1 неэффективен он выполняет асимптотически больше работы (логарифмический коэффициент), чем требуется последовательно. Следовательно, Алгоритм 1 предпочтительнее, когда возможна реализация большого количества параллельных процессов, иначе имеет преимущество Алгоритм 2.

Параллельные алгоритмы для префиксных сумм часто могут быть обобщены на другие ассоциативные двоичные операции сканирования,^[3]^[4], и они также могут быть эффективно вычислены на современном параллельном оборудовании, таком как GPU (Графический процессор).^[11] Идея создания в аппаратном обеспечении функционального блока, предназначенного для вычисления многопараметрической префиксной суммы, была запатентована Узи Вишкиным.^[12]

Многие параллельные реализации используют двухэтапную процедуру, в которой частичная префиксная сумма вычисляются в первом этапе для каждого блока обработки; префиксная сумма этих частичных сумм затем вычисляется и передается обратно в блоки обработки для второго этапа, используя теперь известный префикс в качестве начального значения. Асимптотически этот метод занимает примерно две операции чтения и одну операцию записи для каждого элемента.

Реализации алгоритмов для вычисления префиксных сумм

Реализация алгоритма параллельного вычисления префиксной суммы, как и другие параллельные алгоритмы, должна учитывать архитектуру распараллеливания платформы. Существует множество алгоритмов, которые адаптированы для платформ, работающих с разделяемой памятью, а также алгоритмы, которые хорошо подходят для платформ, использующих распределенную память, пользуясь при этом обменом сообщений в качестве единственной формы межпроцессного взаимодействия.

Разделяемая память: двухуровневый алгоритм

Следующий алгоритм предполагает модель машины с разделяемой памятью; все обрабатывающие элементы PE (от англ. processing elements) имеют доступ к одной и той же памяти. Вариант этого алгоритма реализован в многоядерной стандартной библиотеке шаблонов (MCSTL)^[13]^[14], параллельной реализации стандартной библиотеки шаблонов C++, которая предоставляет адаптированные версии для параллельных вычислений различных алгоритмов.

Чтобы одновременно вычислить префиксную сумму из [math]\displaystyle{ n }[/math] элементов данных с [math]\displaystyle{ p }[/math] элементами обработки, данные делятся на [math]\displaystyle{ p+1 }[/math] блоков, каждый из которых содержит [math]\displaystyle{ \frac n {p+1} }[/math] элементов (для простоты мы будем считать, что [math]\displaystyle{ n }[/math] делится на [math]\displaystyle{ p+1 }[/math]). Обратите внимание, что, хотя алгоритм делит данные на [math]\displaystyle{ p+1 }[/math] блоков, параллельно работают только [math]\displaystyle{ p }[/math] обрабатывающих элементов.

В первом цикле каждый PE вычисляет локальную префиксную сумму для своего блока. Последний блок вычислять не нужно, так как эти префиксные суммы рассчитываются только как смещения префиксных сумм последующих блоков, и последний блок по определению не является подходящим.

Смещенные [math]\displaystyle{ p }[/math], которые хранятся в последней позиции каждого блока, накапливаются в собственной префиксной сумме и сохраняются в последующих позициях. Если [math]\displaystyle{ p }[/math] мало, то последовательный алгоритм выполняется достаточно быстро, для больших [math]\displaystyle{ p }[/math] этот шаг может выполняться параллельно.

Теперь перейдем ко второму циклу. На этот раз первый блок обрабатывать не нужно, так как ему не нужно учитывать смещение предыдущего блока. Однако теперь включается последний блок, и суммы префиксов для каждого блока рассчитываются с учетом смещений блоков суммы префиксов, рассчитанных в предыдущем цикле.

function prefix_sum(elements) {
    n := size(elements)
    p := number of processing elements
    prefix_sum := [0...0] of size n

    do parallel i = 0 to p-1 {
        // i := индекс текущего PE
        from j = i * n / (p+1) to (i+1) * n / (p+1) - 1 do {
            // Здесь хранится префиксная сумма локальных блоков
            store_prefix_sum_with_offset_in(elements, 0, prefix_sum)
        }
    }

    x = 0

    for i = 1 to p {
        x +=  prefix_sum[i * n / (p+1) - 1] // Построение префиксной суммы по первым p блокам
        prefix_sum[i * n / (p+1)] = x       // Сохрание результатов для использования в качестве смещений во втором цикле
    }

    do parallel i = 1 to p {
        // i := индекс текущего PE
        from j = i * n / (p+1) to (i+1) * n / (p+1) - 1 do {
            offset := prefix_sum[i * n / (p+1)]
            // Рассчитывание префиксной суммы в качестве смещения суммы предыдущих блоков
            store_prefix_sum_with_offset_in(elements, offset, prefix_sum)
        }
    }

    return prefix_sum
}

Распределенная память: алгоритм гиперкуба

Алгоритм префиксной суммы гиперкуба^[15] хорошо адаптирован для платформ с распределенной памятью и использует обмен сообщениями между элементами обработки. Предполагается, что в алгоритме участвуют [math]\displaystyle{ p=2^d }[/math] PE , равного числу углов в [math]\displaystyle{ d }[/math]-мерном гиперкубе.

Различные гиперкубы для разного количества узлов

На протяжении всего алгоритма каждый PE рассматривается как угол в гипотетическом гиперкубе со знанием общей префиксной суммы [math]\displaystyle{ \sigma }[/math], а также префиксной суммы [math]\displaystyle{ x }[/math] всех элементов до самого себя (в соответствии с упорядоченными индексами среди PE), каждая в свой гиперкуб.

Алгоритм начинается с предположения, что каждый PE является единственным углом нульмерного гиперкуба и, следовательно, [math]\displaystyle{ \sigma }[/math] и [math]\displaystyle{ x }[/math] равны сумме локального префикса его собственных элементов.
Алгоритм продолжается объединением гиперкубов, смежных по одному измерению. Во время каждого объединения [math]\displaystyle{ \sigma }[/math] обменивается и суммируется между двумя гиперкубами, что сохраняет инвариант того, что все PE в углах этого нового гиперкуба хранят общую префиксную сумму объединенного гиперкуба в своей переменной [math]\displaystyle{ \sigma }[/math]. Однако только гиперкуб, содержащий PE с более высокими индексами, добавляет это [math]\displaystyle{ \sigma }[/math] к своей локальной переменной [math]\displaystyle{ x }[/math], сохраняя инвариант. [math]\displaystyle{ x }[/math] хранит только значение суммы префикса всех элементов в PE с индексами, меньшими или равными их собственному индексу.

В [math]\displaystyle{ d }[/math]-мерном гиперкубе с [math]\displaystyle{ 2^d }[/math] PE по углам алгоритм должен повторяться [math]\displaystyle{ d }[/math] раз, чтобы [math]\displaystyle{ 2^d }[/math] нульмерных гиперкуба были объединены в один [math]\displaystyle{ d }[/math]-мерный гиперкуб. Предполагая модель дуплексной связи, в которой [math]\displaystyle{ \sigma }[/math] двух смежных PE в разных гиперкубах можно обменивать в обоих направлениях за один шаг связи, это означает, что [math]\displaystyle{ d=\log_2 p }[/math] запусков связи.

i := Index of own processor element (PE)
m := prefix sum of local elements of this PE
d := number of dimensions of the hyper cube

x = m;     // Инвариант: префиксная сумма PE в текущем вложенном кубе
σ = m;     // Инвариант: префиксная сумма всех элементов в текущем вложенном кубе

for (k=0; k <= d-1; k++){
    y = σ @ PE(i xor 2^k)  // Получение общей суммы префикса противоположного вложенного куба по измерению k
    σ = σ + y              // Суммирование префиксных сумм обоих вложенных кубов

    if (i & 2^k){
        x = x + y  // Суммирование префиксной суммы из другого вложенного куба только в том случае, если этот PE является индексом с более     высоким индексом
    }
}

Большие размеры сообщений: конвейерное двоичное дерево

Конвейерный алгоритм двоичного дерева^[16] — это еще один алгоритм для платформ с распределенной памятью, который особенно хорошо подходит для сообщений большого размера.

Как и алгоритм гиперкуба, он предполагает особую коммуникационную структуру. PE гипотетически расположены в двоичном дереве (например, в дереве Фибоначчи) с инфиксной нумерацией в соответствии с их индексом в PE. Связь в таком дереве всегда происходит между родительским и дочерним узлами.

Инфиксная нумерация гарантирует, что для любого данного PE_j индексы всех узлов достижимы его левым поддеревом [math]\displaystyle{ \mathbb{[l...j-1]} }[/math] меньше [math]\displaystyle{ j }[/math], а индексы [math]\displaystyle{ \mathbb{[j+1...r]} }[/math] всех узлов в правом поддереве больше [math]\displaystyle{ j }[/math]. Индекс родителя больше, чем любой из индексов в поддереве PE_j, если PE_j — левый потомок, и меньше, если PE_j — правый потомок. Это допускает следующие рассуждения:

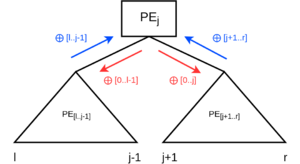
Локальная префиксная сумма [math]\displaystyle{ \mathbb{\oplus[l..j-1]} }[/math] левого поддерева должна быть объединена для вычисления суммы локального префикса PE_j [math]\displaystyle{ \mathbb{\oplus[l..j]} }[/math].
Локальная префиксная сумма [math]\displaystyle{ \mathbb{\oplus[j+1..r]} }[/math] правого поддерева должна быть объединена для вычисления суммы локального префикса PE_h более высокого уровня, которая достигается на пути, содержащем левое дочернее соединение (это означает, что [math]\displaystyle{ h \gt j }[/math]).
Общая сумма префикса [math]\displaystyle{ \mathbb{\oplus[0..j]} }[/math] для PE_j необходима для вычисления общей суммы префикса в правом поддереве (например, [math]\displaystyle{ \mathbb{\oplus[0..j..r]} }[/math] для самого высокого индексного узла в поддереве).
PE_j должен включать общую префиксную сумму [math]\displaystyle{ \mathbb{\oplus[0..l-1]} }[/math] первого узла более высокого порядка, который достигается по восходящему пути, включающему соединение правых дочерних элементов, чтобы вычислить его общую префиксную сумму.

Обратите внимание на различие между поддерево-локальной и общей префиксной суммой. Точки два, три и четыре могут привести к тому, что они сформируют круговую зависимость, но это не так. PE нижних уровней могут потребовать, чтобы общая префиксная сумма PE верхних уровней вычисляла их общую префиксную сумму, но PE верхних уровней требуют только локальную префиксную сумму поддерева для вычисления их общей префиксной суммы. Корневой узел как узел самого высокого уровня требует только локальную префиксную сумму своего левого поддерева для вычисления своей собственной префиксной суммы. Каждый PE на пути от PE₀ к корневому PE требует только локальную префиксную сумму своего левого поддерева для вычисления своей собственной префиксной суммы, в то время как каждому узлу на пути от PE_p-1 (последнего PE) до PE_root требуется общая префиксная сумма его родителя, чтобы вычислить его собственную общую префиксную сумму.

Это приводит к двухфазному алгоритму:

Восходящая фаза
Распространение локальной префиксной суммы поддерева [math]\displaystyle{ \mathbb{\oplus[l..j..r]} }[/math] его родителю для каждого PE_j.

Нисходящая фаза
Распространение эксклюзивной (эксклюзивный PE_j, а также PE в его левом поддереве) суммарной префиксной суммы [math]\displaystyle{ \mathbb{\oplus[0..l-1]} }[/math] всех PE с более низкими индексами, которые не включены в адресуемое поддерево PE_j, на PE более низких уровней левого дочернего поддерева PE_j. Распространение инклюзивной префиксной суммы ⊕ [0…j] на правое дочернее поддерево PE_j.

Стоит отметить, что алгоритм выполняется на каждом PE и PE будут ждать пока все пакеты от всех дочерних/родительских элементов не будут получены.

k := number of packets in a message m of a PE
m @ {left, right, parent, this} := // Сообщения в разные PE

x = m @ this

// Восходящая фаза- рассчитывание локальной префиксной суммы поддерева
for j=0 to k-1: // Конвейерная передача: для каждого пакета сообщения
    if hasLeftChild:
        blocking receive m[j] @ left // Замена локального m[j] полученным m[j]
        // Совокупная инклюзивная локальная префиксная сумма из PE с более низкими индексами
        x[j] = m[j] ⨁ x[j] 

    if hasRightChild:
        blocking receive m[j] @ right
        // Мы не объединяем m[j] в локальную префиксную сумму, так как правильные потомки - это PE с более высокими индексами
        send x[j] ⨁ m[j] to parent
    else:
        send x[j] to parent

// Нисходящая фаза
for j=0 to k-1:
    m[j] @ this = 0

    if hasParent:
        blocking receive m[j] @ parent
        // Для левого ребенка m[j] - родительская эксклюзивная префиксная сумма, для правого ребенка - инклюзивная префиксная сумма
        x[j] = m[j] ⨁ x[j] 

    send m[j] to left  // Общая префиксная сумма всех PE, меньших, чем этот или любой PE в левом поддереве
    send x[j] to right // Общая префиксная сумма всех PE меньше или равных этому PE

Конвейерная передача

Конвейерная передача может быть применена в случае, когда сообщение [math]\displaystyle{ m }[/math] длины [math]\displaystyle{ n }[/math] может быть разделено на [math]\displaystyle{ k }[/math] частей и оператор ⨁ может быть применен к каждой такой части отдельно.^[16]

Если алгоритм используется без конвейерной передачи, то в дереве в любой момент времени работают только два уровня(отправляющий PE и принимающий PE), в то время как остальные РЕ ожидают. Если используется бинарное сбалансированное дерево [math]\displaystyle{ p }[/math] обрабатывающих элементов, содержащее [math]\displaystyle{ \log _{2}p }[/math] уровней, то длина пути от [math]\displaystyle{ PE_0 }[/math] до [math]\displaystyle{ PE_\mathbb{root} }[/math] [math]\displaystyle{ \log _{2}p - 1 }[/math], что соответствует максимальному числу непараллельных операций связи восходящей фазы. Аналогично связи по нисходящему пути также ограничены этим же значением. Считая время запуска связи [math]\displaystyle{ T_\mathbb{start} }[/math] и байтовое время передачи [math]\displaystyle{ T_\mathbb{byte} }[/math] получим, что фазы ограничены по времени [math]\displaystyle{ (2\log _{2}p-2)(T_\mathbb{start} + n\cdot T_\mathbb{byte}) }[/math] в неконвейерной передаче. При делении на [math]\displaystyle{ k }[/math] частей, каждый из которых имеет [math]\displaystyle{ \frac{n}{k} }[/math] элементов и отправляет их независимо друг от друга, первая часть будет требовать [math]\displaystyle{ (\log _{2}p-1)(T_\mathbb{start} + \frac{n}{k} \cdot T_\mathbb{byte}) }[/math] для прохождения к [math]\displaystyle{ PE_{\mathbb{root}} }[/math] как часть локальной префиксной суммы и такое время будет действительно для последней части, если [math]\displaystyle{ k \gt \log_{2}p }[/math].

В остальных частях все РЕ могут работать параллельно и каждая третья операция взаимодействия(получение слева, получения справа, отправка родителю) отправляет пакет на следующий уровень, поэтому одна фаза может быть проделана за [math]\displaystyle{ 2\log_{2}p-1 + 3(k-1) }[/math] операций взаимодействия и обе фазы вместе требуют [math]\displaystyle{ (4\cdot \log_{2}p-2 + 6(k-1))(T_\mathbb{start} + \frac{n}{k} \cdot T_\mathbb{byte}) }[/math], что является очень хорошим показателем для сообщений длины [math]\displaystyle{ n }[/math].

Алгоритм может быть дополнительно оптимизирован путем использования полнодуплексной или телекоммуникационной модели связи и перекрытия восходящей и нисходящей фазы.^[16]

Структуры данных

При необходимости динамического обновления набора данных, ее можно хранить в дереве Фенвика. Такая структура данных позволяет за логарифмическое время не только находить любое значение префиксной суммы, но и изменять любое значение элемента в массиве.^[17]. Так как в 1982 термин префиксной суммы еще не был достаточно распространен, появилась работа^[18], где была представлена структура данных, называемая Деревом частичных сумм (5.1), которая заменяла название дерева Фенвика.

Для вычисления сумм произвольных прямоугольных подмассивов на многомерных массивах, таблица суммированных площадей представляется структурой данных, построенной на префиксных суммах. Такая таблица может быть полезна в задачах свертки изображений.^[19]

Приложения

Сортировка подсчетом — это алгоритм целочисленной сортировки, который использует префиксную сумму гистограммы ключевых частот для вычисления положения каждого ключа в отсортированном выходном массиве. Он работает за линейное время для целочисленных ключей, которые меньше числа элементов, и часто используется как часть поразрядной сортировки, быстрого алгоритма сортировки целых чисел, которые менее ограничены по величине.^[1]

Ранжирование списка, задача преобразования связного списка в массив, содержащий ту же последовательность элементов, может рассматриваться как префиксные суммы на последовательности единиц, а затем сопоставление каждого элемента с позицией в массиве, полученной из значения его префиксной суммы. Много важных задан на деревьях могут быть решены на параллельных алгоритмах путем совмещения ранжирования списков, префиксных сумм и обходов Эйлера.^[4]

Параллельное вычисление префиксных сумм также используется в разработке двоичных сумматоров, логических схем, которые могут складывать два n-битных двоичных числа. В этом случае, последовательность битов переноса сложения может быть представлена как операция сканирования на последовательности пар входных битов с использованием функции большинства для объединения данного переноса с этими двумя битами. Каждый бит выходного числа может быть найден как эксклюзивный дизъюнктор двух входных битов с соответствующим переносом битов. Таким образом можно сконструировать сумматор, который использует O(n) логических элементов и O(log n) временных шагов.^[3]^[9]^[10]

В модели вычислительных машин с параллельным произвольным доступом, префиксные суммы могут использоваться для моделирования параллельных алгоритмов, которые предполагают возможность для нескольких процессоров одновременно обращаться к одной и той же ячейке памяти на параллельных машинах, которые запрещают одновременный доступ. Посредством сети сортировки, набор параллельных запросов на доступ к памяти может быть упорядочен в последовательность, так что доступ к одной и той же ячейке является непрерывным в пределах последовательности. Затем можно использовать операции сканирования, чтобы определить, какой из обращений записи в запрошенные ячейки завершился успешно, и распределить результаты операций чтения из памяти по нескольким процессорам, которые запрашивают один и тот же результат.^[20]

В докторской диссертации Гая Блеллока^[21] параллельные префиксные операции являются частью формализации модели параллелизма данных, предоставляемой машинами, такими как Connection Machine. Connection Machine CM-1 и CM-2 предоставила гиперкубическую сеть, в которой мог быть реализован вышеупомянутый алгоритм 1, тогда как CM-5 предоставил сеть для реализации алгоритма 2.^[22]

При построении кодов Грея, последовательностей двоичных значений со свойством того, что значения последовательных последовательностей отличаются друг от друга в одной битовой позиции, число n может быть преобразовано в значение кода Грея в позиции n, просто взяв исключающее «или» n и n/2 (число, образованное смещением n вправо на одну битовую позицию). Обратная операция, декодирующая кодированное по Грею значение x в двоичное число, является более сложной, но может быть выражена как префиксная сумма битов x, где каждая операция суммирования в пределах префиксной суммы выполняется по модулю два. Префиксная сумма этого типа может быть эффективно выполнена с использованием побитовых логических операций, доступных на современных компьютерах, путем вычисления исключающего «или» или x с каждым из чисел, образованных смещением x влево на число битов, которое является степенью двух.

Параллельный префикс (с использованием умножения в качестве основной ассоциативной операции) также можно использовать для построения быстрых алгоритмов параллельной полиномиальной интерполяции. В частности, его можно использовать для вычисления коэффициентов деления разности в форме Ньютона интерполяционного полинома.^[23] Этот подход, основанный на префиксах, может также использоваться для получения обобщенных разделенных разностей для (конфлюентной) интерполяции Эрмита, а также для параллельных алгоритмов для систем Вандермонда.

См. также

GPGPU

Примечания

↑ ^1,0 ^1,1 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001), 8.2 Counting Sort, Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, с. 168–170, ISBN 0-262-03293-7 .
↑ Cole, Richard & Vishkin, Uzi (1986), Deterministic coin tossing with applications to optimal parallel list ranking, Information and Control Т. 70 (1): 32–53, DOI 10.1016/S0019-9958(86)80023-7
↑ ^3,0 ^3,1 ^3,2 ^3,3 ^3,4 Ladner, R. E. & Fischer, M. J. (1980), Parallel Prefix Computation, Journal of the ACM Т. 27 (4): 831–838, DOI 10.1145/322217.322232 .
↑ ^4,0 ^4,1 ^4,2 Tarjan, Robert E. & Vishkin, Uzi (1985), An efficient parallel biconnectivity algorithm, SIAM Journal on Computing Т. 14 (4): 862–874, DOI 10.1137/0214061 .
↑ Lakshmivarahan, S. & Dhall, S.K. (1994), Parallelism in the Prefix Problem, Oxford University Press, ISBN 0-19508849-2, <https://archive.org/details/parallelcomputin0000laks> .
↑ Blelloch, Guy (2011), Prefix Sums and Their Applications (Lecture Notes), Carnegie Mellon University, <https://www.cs.cmu.edu/afs/cs/academic/class/15750-s11/www/handouts/PrefixSumBlelloch.pdf> Архивная копия от 14 июня 2021 на Wayback Machine.
↑ Callahan, Paul & Kosaraju, S. Rao (1995), A Decomposition of Multi-Dimensional Point Sets with Applications to k-Nearest-Neighbors and n-Body Potential Fields, Journal of the ACM Т. 42 (1): 67–90, DOI 10.1145/200836.200853 .
↑ Hillis, W. Daniel; Steele, Jr., Guy L. Data parallel algorithms (англ.) // Communications of the ACM. — 1986. — December (vol. 29, no. 12). — P. 1170—1183. — doi:10.1145/7902.7903.
↑ ^9,0 ^9,1 Ofman, Yu. (1962), Doklady Akademii Nauk SSSR Т. 145 (1): 48–51 . English translation, «On the algorithmic complexity of discrete functions», Soviet Physics Doklady 7: 589—591 1963.
↑ ^10,0 ^10,1 Khrapchenko, V. M. (1967), Asymptotic Estimation of Addition Time of a Parallel Adder, Problemy Kibernet. Т. 19: 107–122 . English translation in Syst. Theory Res. 19; 105—122, 1970.
↑ Scan primitives for GPU computing // (Proc. 22nd ACM SIGGRAPH/EUROGRAPHICS Symposium on Graphics Hardware). — 2007. — P. 97–106.
↑ Prefix sums and an application thereof // (U.S. Patent 6,542,918). — 2003.
↑ Singler, Johannes MCSTL: The Multi-Core Standard Template Library (неопр.). Дата обращения: 29 марта 2019. Архивировано 3 ноября 2016 года.
↑ Singler, Johannes; Sanders, Peter; Putze, Felix. MCSTL: The Multi-core Standard Template Library // Euro-Par 2007 Parallel Processing. — 2007. — Т. 4641. — С. 682—694. — (Lecture Notes in Computer Science). — ISBN 978-3-540-74465-8. — doi:10.1007/978-3-540-74466-5_72.
↑ Ananth Grama; Vipin Kumar; Anshul Gupta. Introduction to Parallel Computing. — Addison-Wesley, 2003. — С. 85, 86. — ISBN 978-0-201-64865-2.
↑ ^16,0 ^16,1 ^16,2 Sanders, Peter; Träff, Jesper Larsson. Parallel Prefix (Scan) Algorithms for MPI // Recent Advances in Parallel Virtual Machine and Message Passing Interface (англ.). — 2006. — Vol. 4192. — P. 49—57. — (Lecture Notes in Computer Science). — ISBN 978-3-540-39110-4. — doi:10.1007/11846802_15.
↑ Fenwick, Peter M. (1994), A new data structure for cumulative frequency tables, Software: Practice and Experience Т. 24 (3): 327–336, DOI 10.1002/spe.4380240306
↑ Shiloach, Yossi & Vishkin, Uzi (1982b), An O(n² log n) parallel max-flow algorithm, Journal of Algorithms Т. 3 (2): 128–146, DOI 10.1016/0196-6774(82)90013-X
↑ Szeliski, Richard (2010), Summed area table (integral image), Computer Vision: Algorithms and Applications, Texts in Computer Science, Springer, с. 106–107, ISBN 9781848829350, <https://books.google.com/books?id=bXzAlkODwa8C&pg=PA106> .
↑ Vishkin, Uzi (1983), Implementation of simultaneous memory address access in models that forbid it, Journal of Algorithms Т. 4 (1): 45–50, DOI 10.1016/0196-6774(83)90033-0 .
↑ Blelloch, Guy E.^[англ.]. Vector models for data-parallel computing (каталан.). — Cambridge, MA: MIT Press, 1990. — ISBN 026202313X.
↑ Leiserson, Charles E.; Abuhamdeh, Zahi S.; Douglas, David C.; Feynman, Carl R.; Ganmukhi, Mahesh N.; Hill, Jeffrey V.; Hillis, W. Daniel^[англ.]; Kuszmaul, Bradley C.; St. Pierre, Margaret A. The Network Architecture of the Connection Machine CM-5 (англ.) // Journal of Parallel and Distributed Computing : journal. — 1996. — 15 March (vol. 33, no. 2). — P. 145—158. — ISSN 0743-7315. — doi:10.1006/jpdc.1996.0033.
↑ Eğecioğlu, O.; Gallopoulos, E. & Koç, C. (1990), A parallel method for fast and practical high-order Newton interpolation, BIT Computer Science and Numerical Mathematics Т. 30 (2): 268–288, DOI 10.1007/BF02017348 .

Ссылки

Weisstein, Eric W. Cumulative Sum (англ.) на сайте Wolfram MathWorld.

[clrs-1] 1,0 ^1,1 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001), 8.2 Counting Sort, Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, с. 168–170, ISBN 0-262-03293-7 .

[cv86-2] Cole, Richard & Vishkin, Uzi (1986), Deterministic coin tossing with applications to optimal parallel list ranking, Information and Control Т. 70 (1): 32–53, DOI 10.1016/S0019-9958(86)80023-7

[lf80-3] 3,0 ^3,1 ^3,2 ^3,3 ^3,4 Ladner, R. E. & Fischer, M. J. (1980), Parallel Prefix Computation, Journal of the ACM Т. 27 (4): 831–838, DOI 10.1145/322217.322232 .

[tv85-4] 4,0 ^4,1 ^4,2 Tarjan, Robert E. & Vishkin, Uzi (1985), An efficient parallel biconnectivity algorithm, SIAM Journal on Computing Т. 14 (4): 862–874, DOI 10.1137/0214061 .

[Prefix.book.92-5] Lakshmivarahan, S. & Dhall, S.K. (1994), Parallelism in the Prefix Problem, Oxford University Press, ISBN 0-19508849-2, <https://archive.org/details/parallelcomputin0000laks> .

[blelloch11-6] Blelloch, Guy (2011), Prefix Sums and Their Applications (Lecture Notes), Carnegie Mellon University, <https://www.cs.cmu.edu/afs/cs/academic/class/15750-s11/www/handouts/PrefixSumBlelloch.pdf> Архивная копия от 14 июня 2021 на Wayback Machine.

[callahan1995-7] Callahan, Paul & Kosaraju, S. Rao (1995), A Decomposition of Multi-Dimensional Point Sets with Applications to k-Nearest-Neighbors and n-Body Potential Fields, Journal of the ACM Т. 42 (1): 67–90, DOI 10.1145/200836.200853 .

[hs1986-8] Hillis, W. Daniel; Steele, Jr., Guy L. Data parallel algorithms (англ.) // Communications of the ACM. — 1986. — December (vol. 29, no. 12). — P. 1170—1183. — doi:10.1145/7902.7903.

[offman-9] 9,0 ^9,1 Ofman, Yu. (1962), Doklady Akademii Nauk SSSR Т. 145 (1): 48–51 . English translation, «On the algorithmic complexity of discrete functions», Soviet Physics Doklady 7: 589—591 1963.

[krapchenko-10] 10,0 ^10,1 Khrapchenko, V. M. (1967), Asymptotic Estimation of Addition Time of a Parallel Adder, Problemy Kibernet. Т. 19: 107–122 . English translation in Syst. Theory Res. 19; 105—122, 1970.

[11] Scan primitives for GPU computing // (Proc. 22nd ACM SIGGRAPH/EUROGRAPHICS Symposium on Graphics Hardware). — 2007. — P. 97–106.

[12] Prefix sums and an application thereof // (U.S. Patent 6,542,918). — 2003.

[13] Singler, Johannes MCSTL: The Multi-Core Standard Template Library (неопр.). Дата обращения: 29 марта 2019. Архивировано 3 ноября 2016 года.

[SinglerSanders2007-14] Singler, Johannes; Sanders, Peter; Putze, Felix. MCSTL: The Multi-core Standard Template Library // Euro-Par 2007 Parallel Processing. — 2007. — Т. 4641. — С. 682—694. — (Lecture Notes in Computer Science). — ISBN 978-3-540-74465-8. — doi:10.1007/978-3-540-74466-5_72.

[GramaKumar2003-15] Ananth Grama; Vipin Kumar; Anshul Gupta. Introduction to Parallel Computing. — Addison-Wesley, 2003. — С. 85, 86. — ISBN 978-0-201-64865-2.

[SandersTraeff2006-16] 16,0 ^16,1 ^16,2 Sanders, Peter; Träff, Jesper Larsson. Parallel Prefix (Scan) Algorithms for MPI // Recent Advances in Parallel Virtual Machine and Message Passing Interface (англ.). — 2006. — Vol. 4192. — P. 49—57. — (Lecture Notes in Computer Science). — ISBN 978-3-540-39110-4. — doi:10.1007/11846802_15.

[17] Fenwick, Peter M. (1994), A new data structure for cumulative frequency tables, Software: Practice and Experience Т. 24 (3): 327–336, DOI 10.1002/spe.4380240306

[18] Shiloach, Yossi & Vishkin, Uzi (1982b), An O(n² log n) parallel max-flow algorithm, Journal of Algorithms Т. 3 (2): 128–146, DOI 10.1016/0196-6774(82)90013-X

[19] Szeliski, Richard (2010), Summed area table (integral image), Computer Vision: Algorithms and Applications, Texts in Computer Science, Springer, с. 106–107, ISBN 9781848829350, <https://books.google.com/books?id=bXzAlkODwa8C&pg=PA106> .

[20] Vishkin, Uzi (1983), Implementation of simultaneous memory address access in models that forbid it, Journal of Algorithms Т. 4 (1): 45–50, DOI 10.1016/0196-6774(83)90033-0 .

[21] Blelloch, Guy E.^[англ.]. Vector models for data-parallel computing (каталан.). — Cambridge, MA: MIT Press, 1990. — ISBN 026202313X.

[22] Leiserson, Charles E.; Abuhamdeh, Zahi S.; Douglas, David C.; Feynman, Carl R.; Ganmukhi, Mahesh N.; Hill, Jeffrey V.; Hillis, W. Daniel^[англ.]; Kuszmaul, Bradley C.; St. Pierre, Margaret A. The Network Architecture of the Connection Machine CM-5 (англ.) // Journal of Parallel and Distributed Computing : journal. — 1996. — 15 March (vol. 33, no. 2). — P. 145—158. — ISSN 0743-7315. — doi:10.1006/jpdc.1996.0033.

[23] Eğecioğlu, O.; Gallopoulos, E. & Koç, C. (1990), A parallel method for fast and practical high-order Newton interpolation, BIT Computer Science and Numerical Mathematics Т. 30 (2): 268–288, DOI 10.1007/BF02017348 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]